LeetCode栈、队列与堆

March 8, 2020 · 9 min read

Ban

ChangAn University

225:使用队列实现栈(Easy)（栈、队列）
使用栈实现队列(East)(栈、队列)
包含min函数的栈(Easy)(栈)
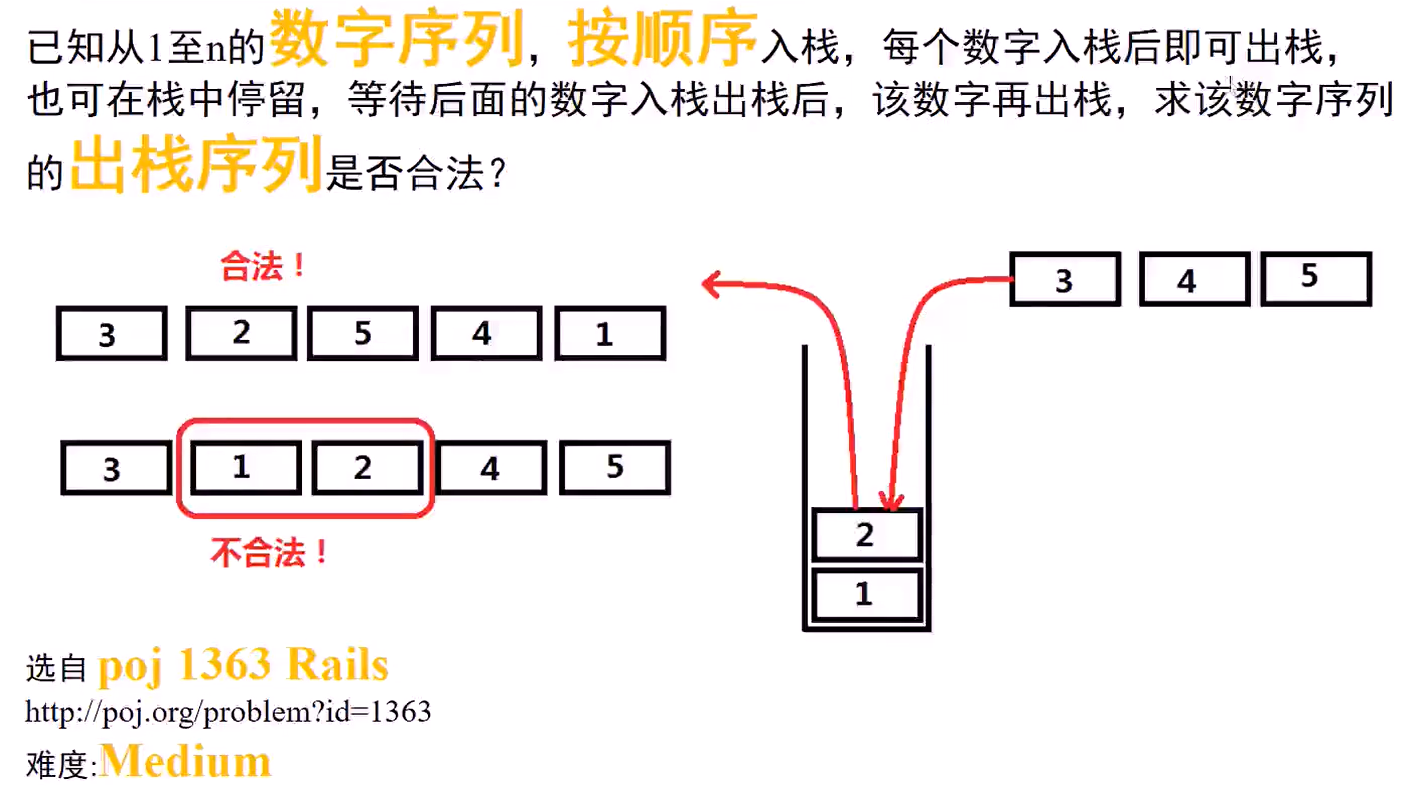
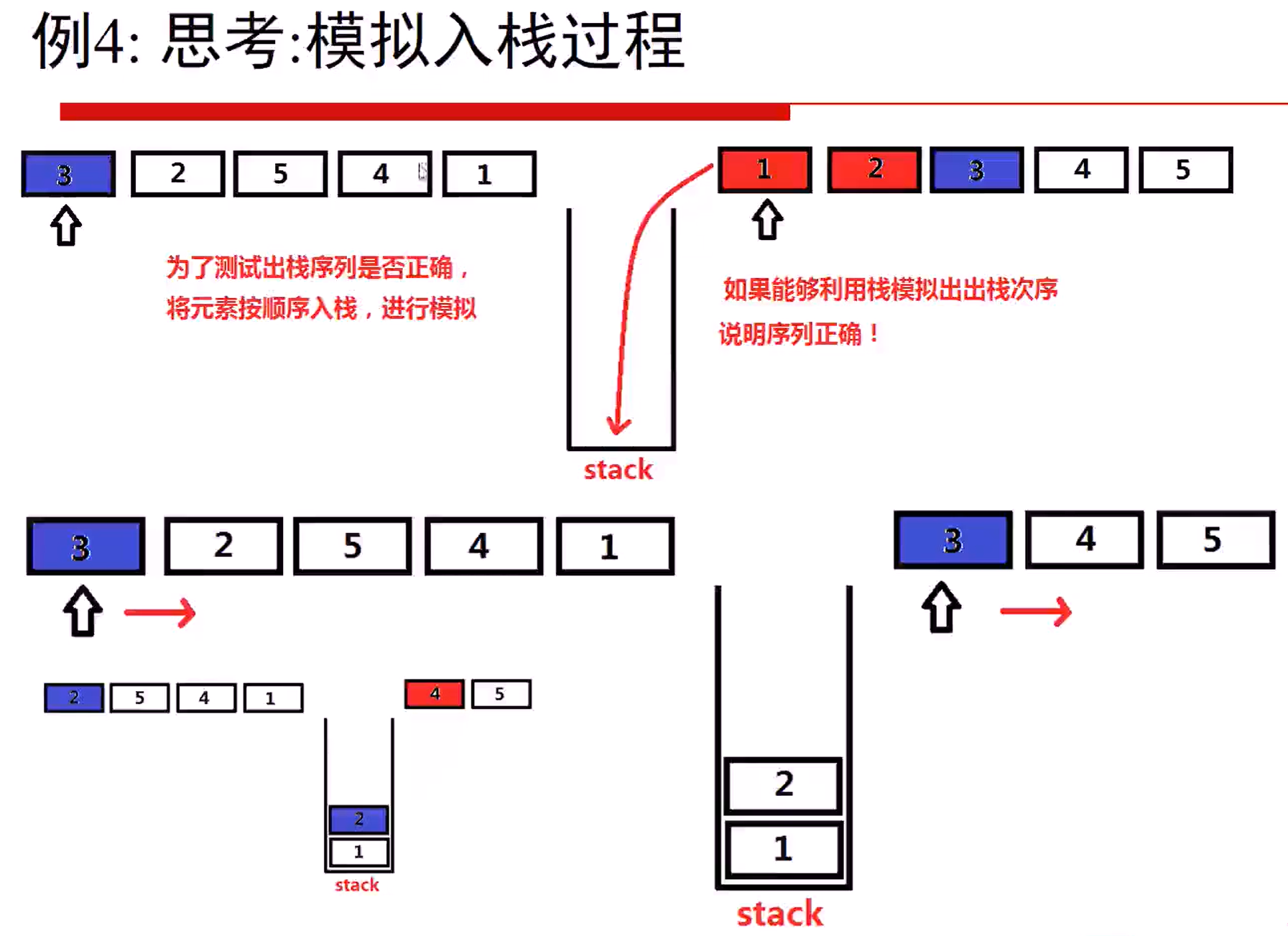
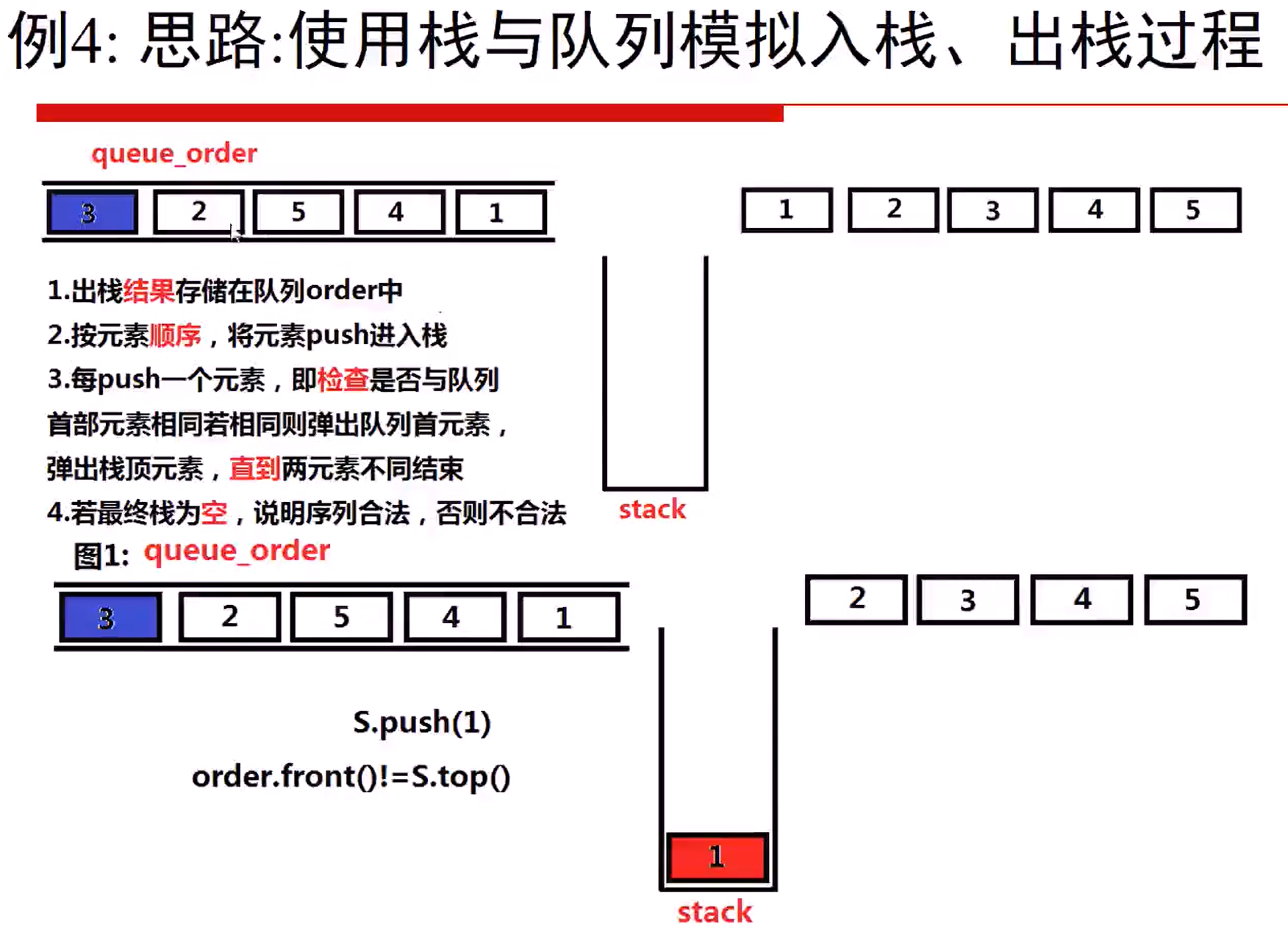
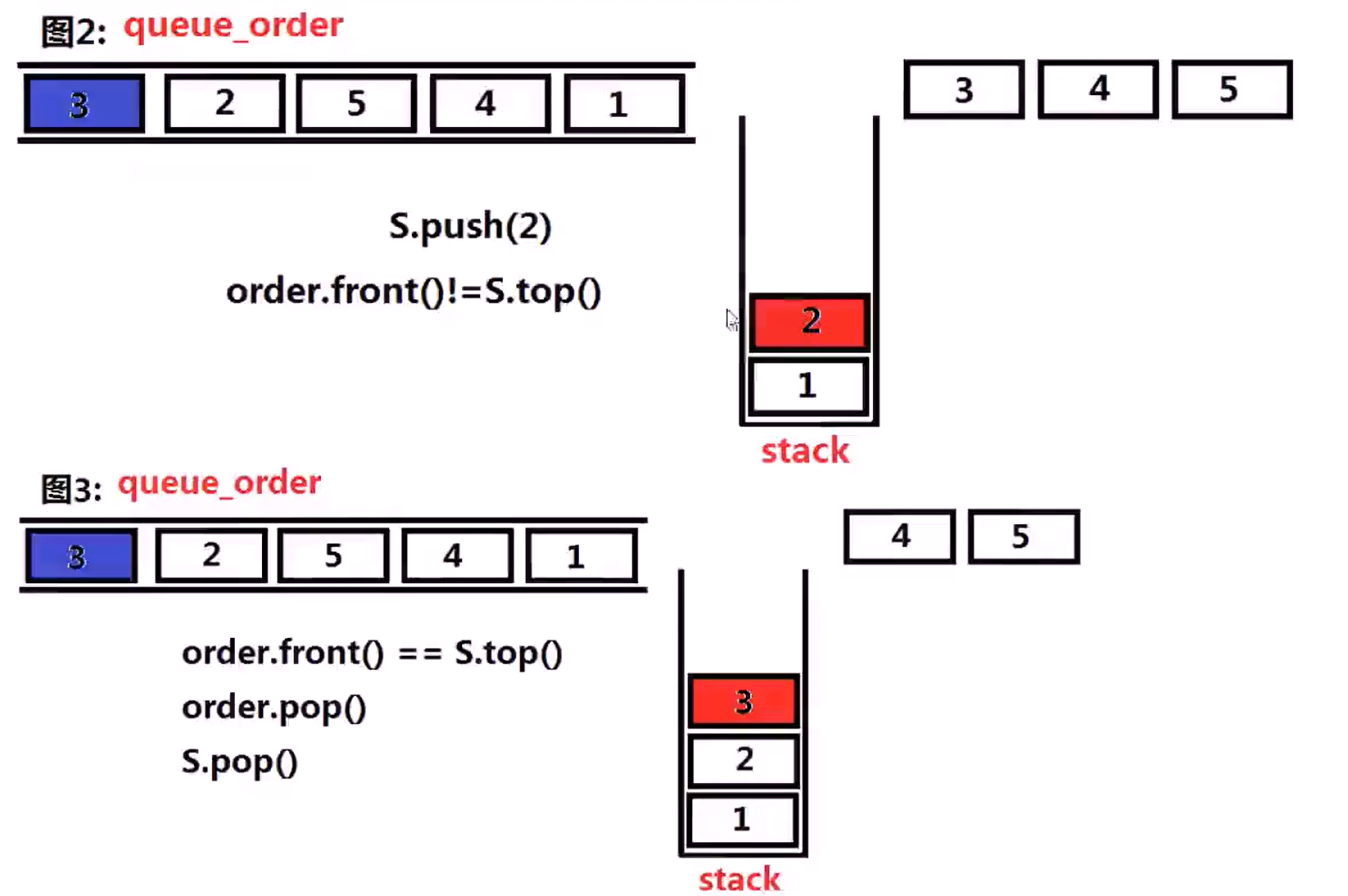
合法的出栈序列(Medium)（栈、队列）
简单的计算器(hard)（栈）
数组中第K大的数(Easy)（堆）
寻找中位数(hard)（堆）

预备知识——栈与队列

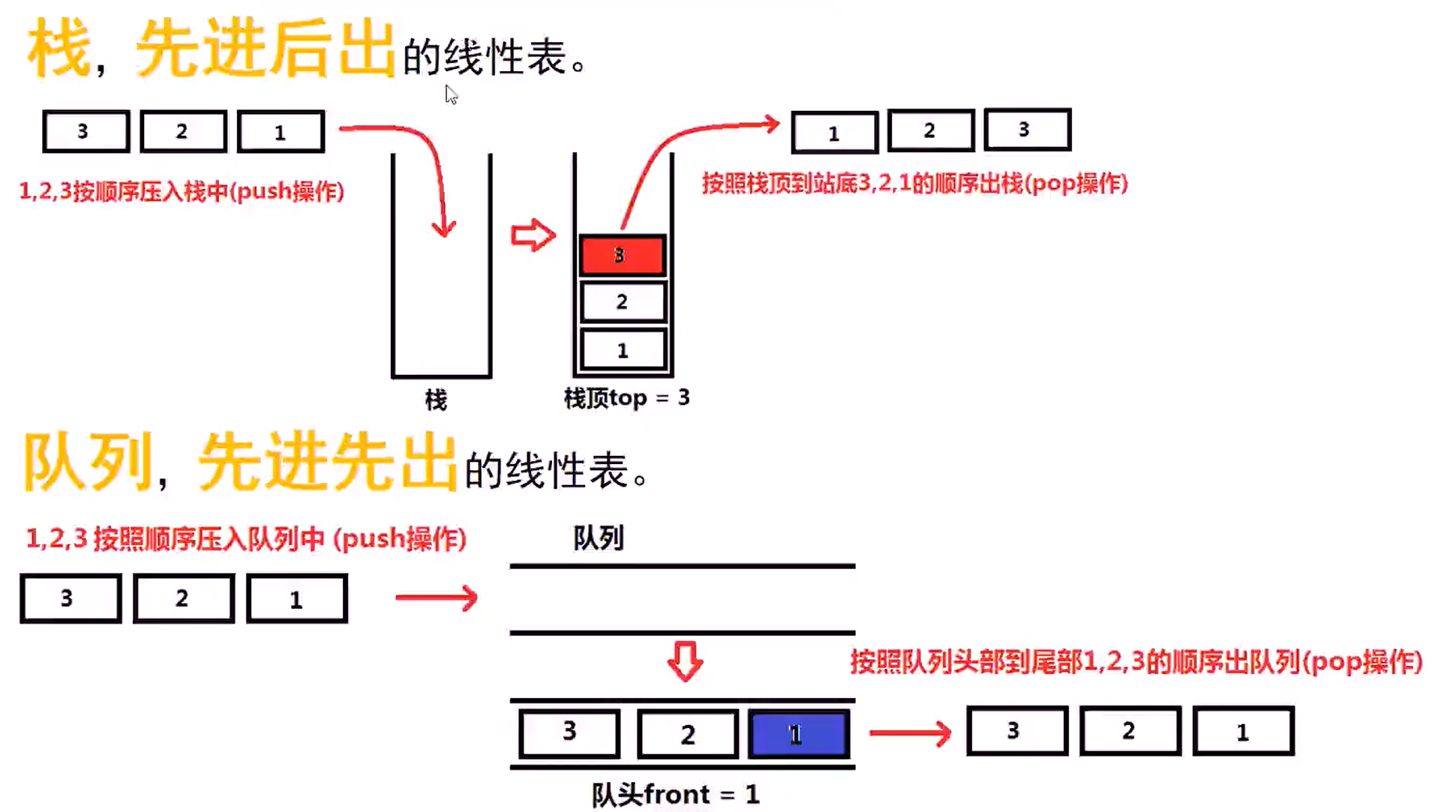
栈

/*
    栈
*/
int main()
{
    stack<int> s;

    if (s.empty())
    {
        printf("stack is empty\n");
    }

    s.push(1);
    s.push(2);
    s.push(3);

    printf("top of stack = %d\n", s.top());
    printf("size of stack = %d\n", s.size());

    s.pop();
    printf("after pop()\n");
    printf("top of stack = %d\n", s.top());
    printf("size of stack = %d\n", s.size());

    return 0;
}

队列

/*
    队列
*/
int main()
{
    queue<int> Q;
    if (Q.empty())
    {
        printf("Queue is empty\n");
    }

    Q.push(1);
    Q.push(2);
    Q.push(3);

    printf("Q.front = %d\n", Q.front());
    printf("Q.back = %d\n", Q.back());

    Q.pop();
    Q.pop();

    printf("Q.front = %d\n", Q.front());
    printf("Q.back = %d\n", Q.back());

    printf("Q.size() = %d\n", Q.size());

    return 0;
}

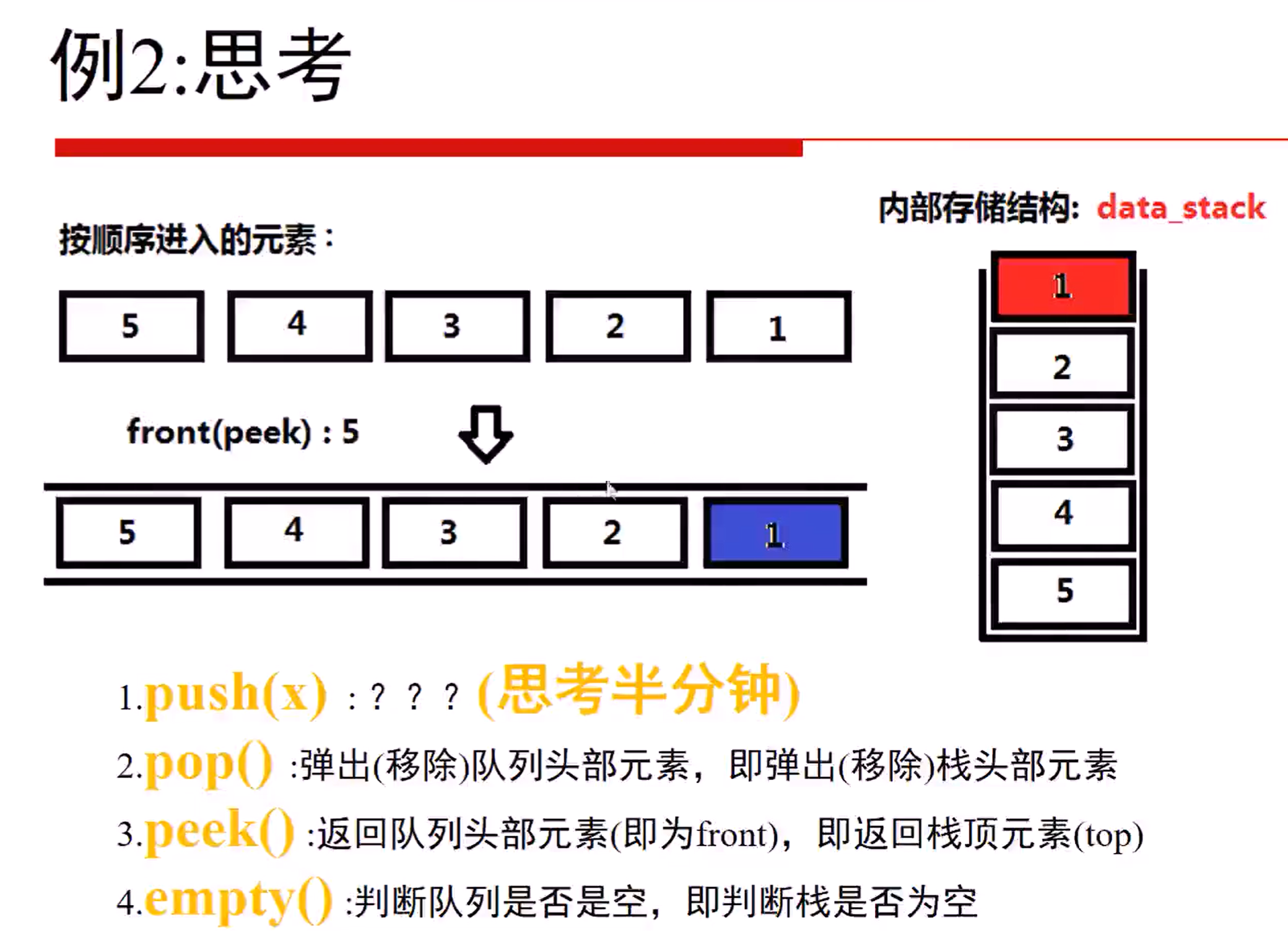
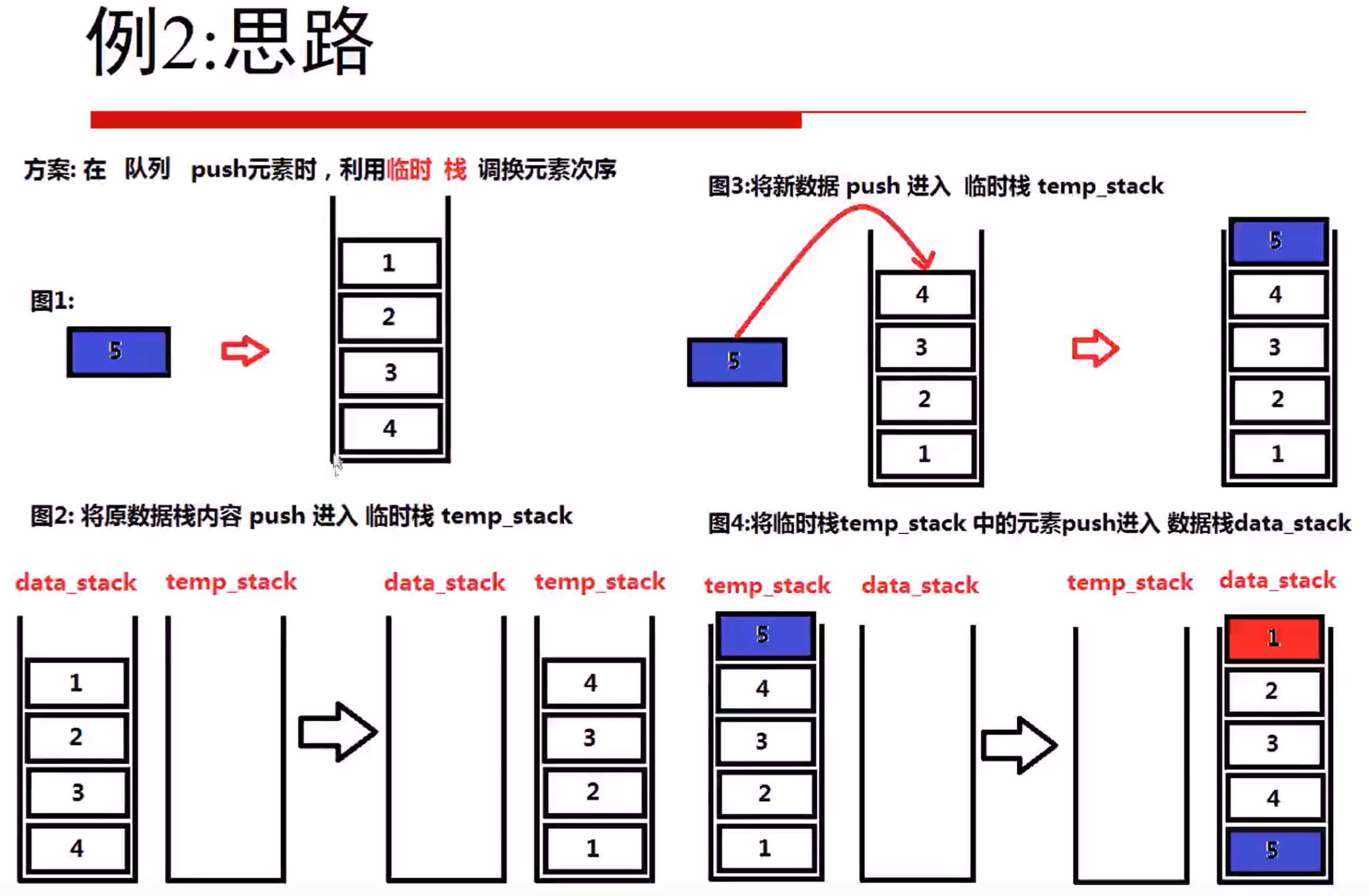
255 Implement Stack using Queues (Easy)

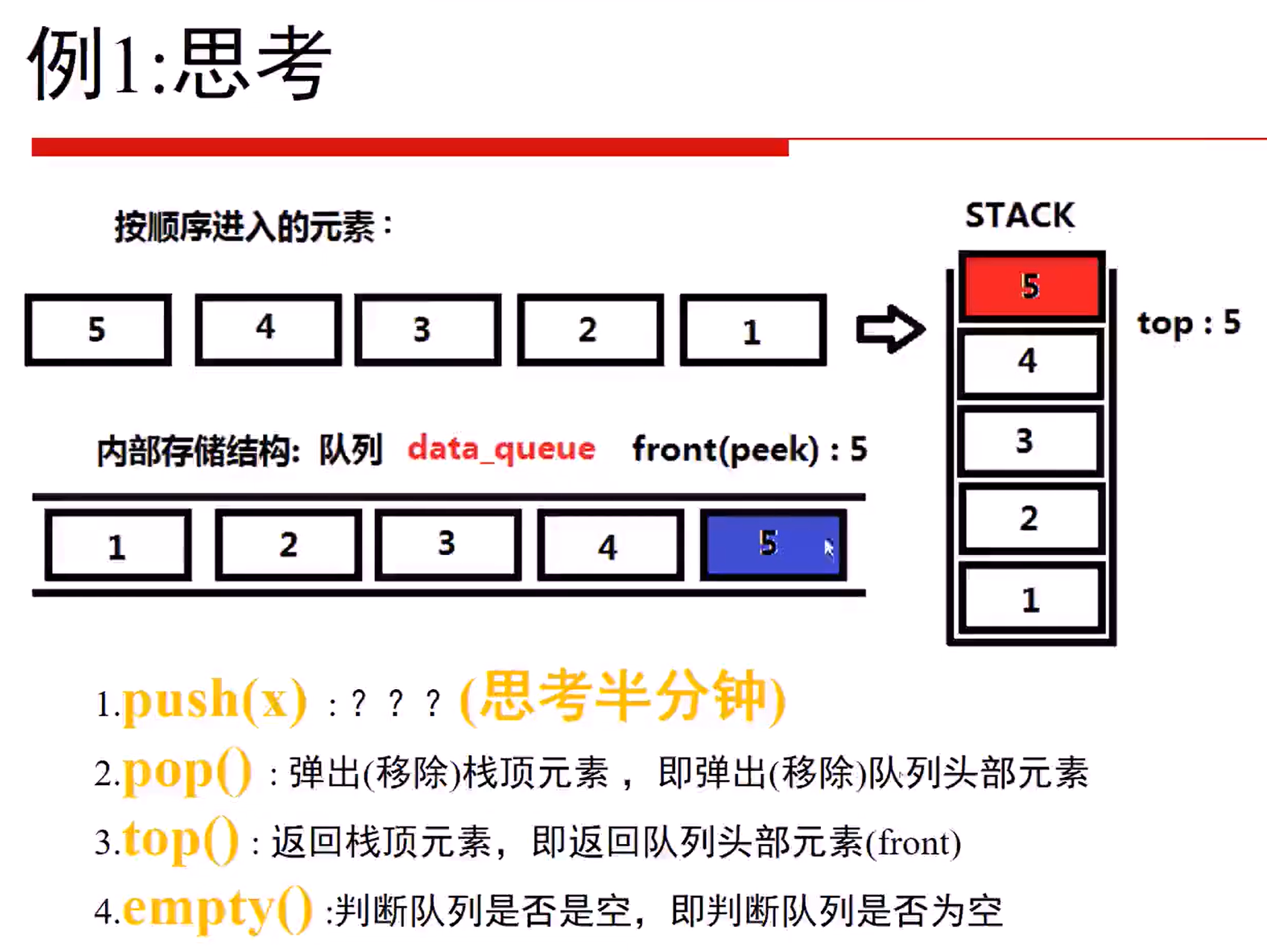
为了让queue的pop()和stack的pop()位置对应，所以我们的内部队列要倒着存

class MyStack
{
private:
    queue<int> Q;

public:
    /** Initialize your data structure here. */
    MyStack()
    {
    }

    /** Push element x onto stack. */
    void push(int x)
    {
        queue<int> temp;
        //1
        temp.push(x);

        while (!Q.empty())
        {
            //2
            temp.push(Q.front());
            Q.pop();
        }

        while (!temp.empty())
        {
            //3
            Q.push(temp.front());
            temp.pop();
        }
    }

    /** Removes the element on top of the stack and returns that element. */
    int pop()
    {
        int x = Q.front();
        Q.pop();
        return x;
    }

    /** Get the top element. */
    int top()
    {
        return Q.front();
    }

    /** Returns whether the stack is empty. */
    bool empty()
    {
        return Q.empty();
    }
};

int main()
{

    MyStack s;
    s.push(1);
    s.push(2);
    s.push(3);

    printf("%d\n", s.top());
    s.pop();
    printf("%d\n", s.top());
    s.push(4);
    printf("%d\n", s.top());

    return 0;
}

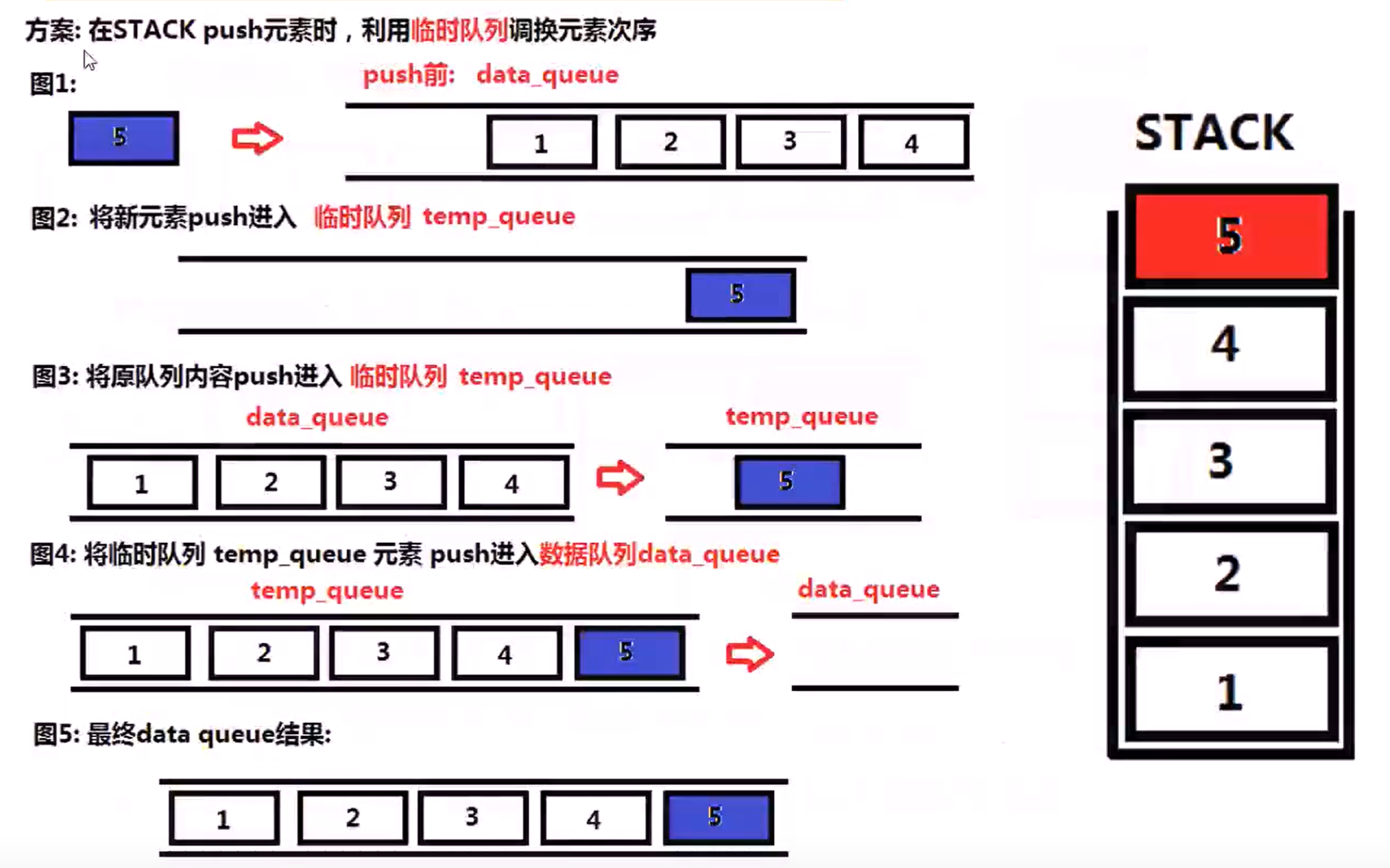
232 Implement Queue using Stacks (Easy)

class MyQueue
{
private:
    stack<int> S;

public:
    /** Initialize your data structure here. */
    MyQueue()
    {
    }

    /** Push element x to the back of queue. */
    void push(int x)
    {
        stack<int> temp;
        while (!S.empty())
        {
            temp.push(S.top());
            S.pop();
        }
        temp.push(x);

        while (!temp.empty())
        {
            S.push(temp.top());
            temp.pop();
        }
    }

    /** Removes the element from in front of queue and returns that element. */
    int pop()
    {
        int x = S.top();
        S.pop();
        return x;
    }

    /** Get the front element. */
    int peek()
    {
        return S.top();
    }

    /** Returns whether the queue is empty. */
    bool empty()
    {
        return S.empty();
    }
};

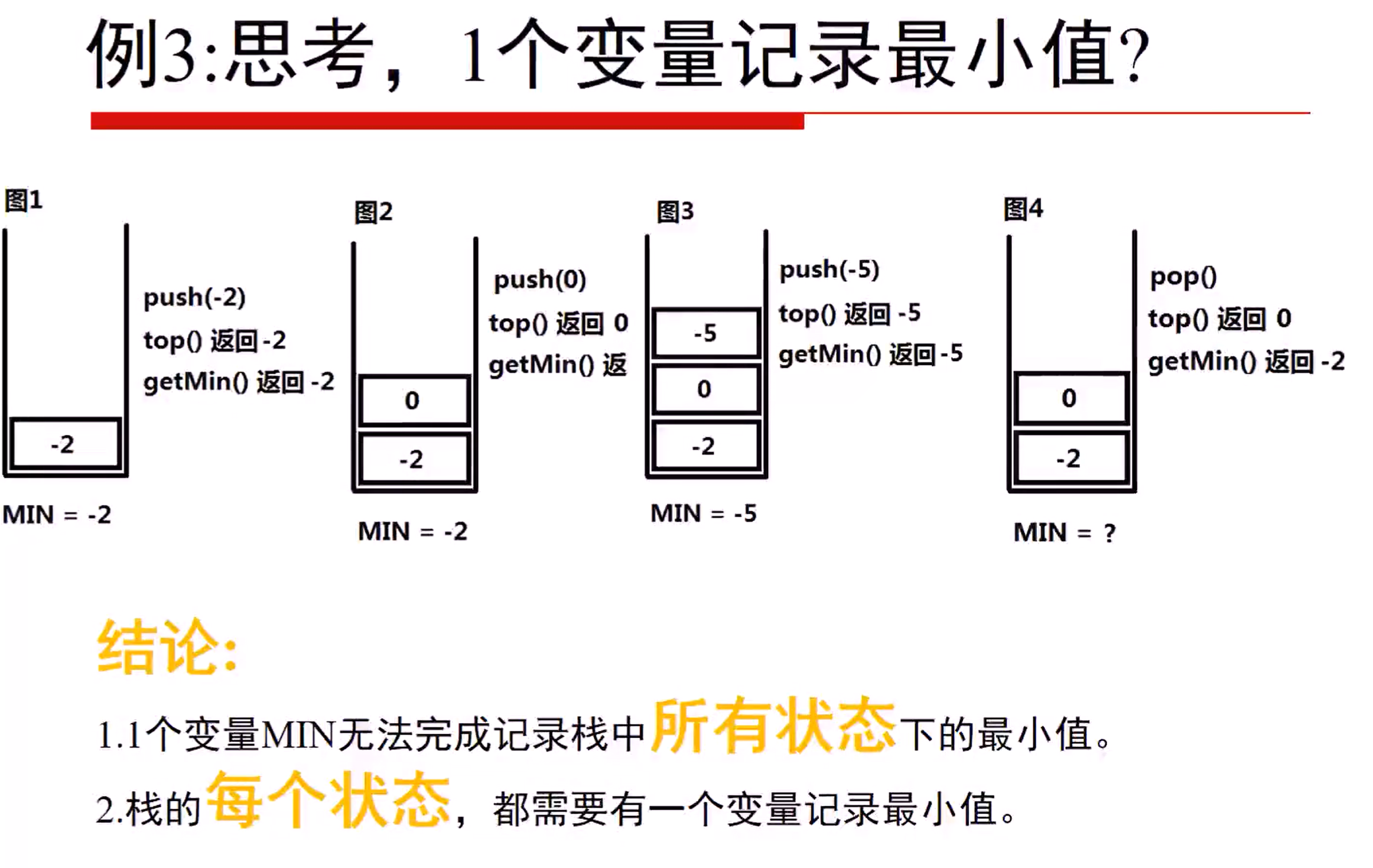
155 Min Stack (Easy)

Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.

push(x) -- Push element x onto stack. pop() -- Removes the element on top of the stack. top() -- Get the top element. getMin() -- Retrieve the minimum element in the stack.

Example:

MinStack minStack = new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.getMin(); --> Returns -3. minStack.pop(); minStack.top(); --> Returns 0. minStack.getMin(); --> Returns -2.

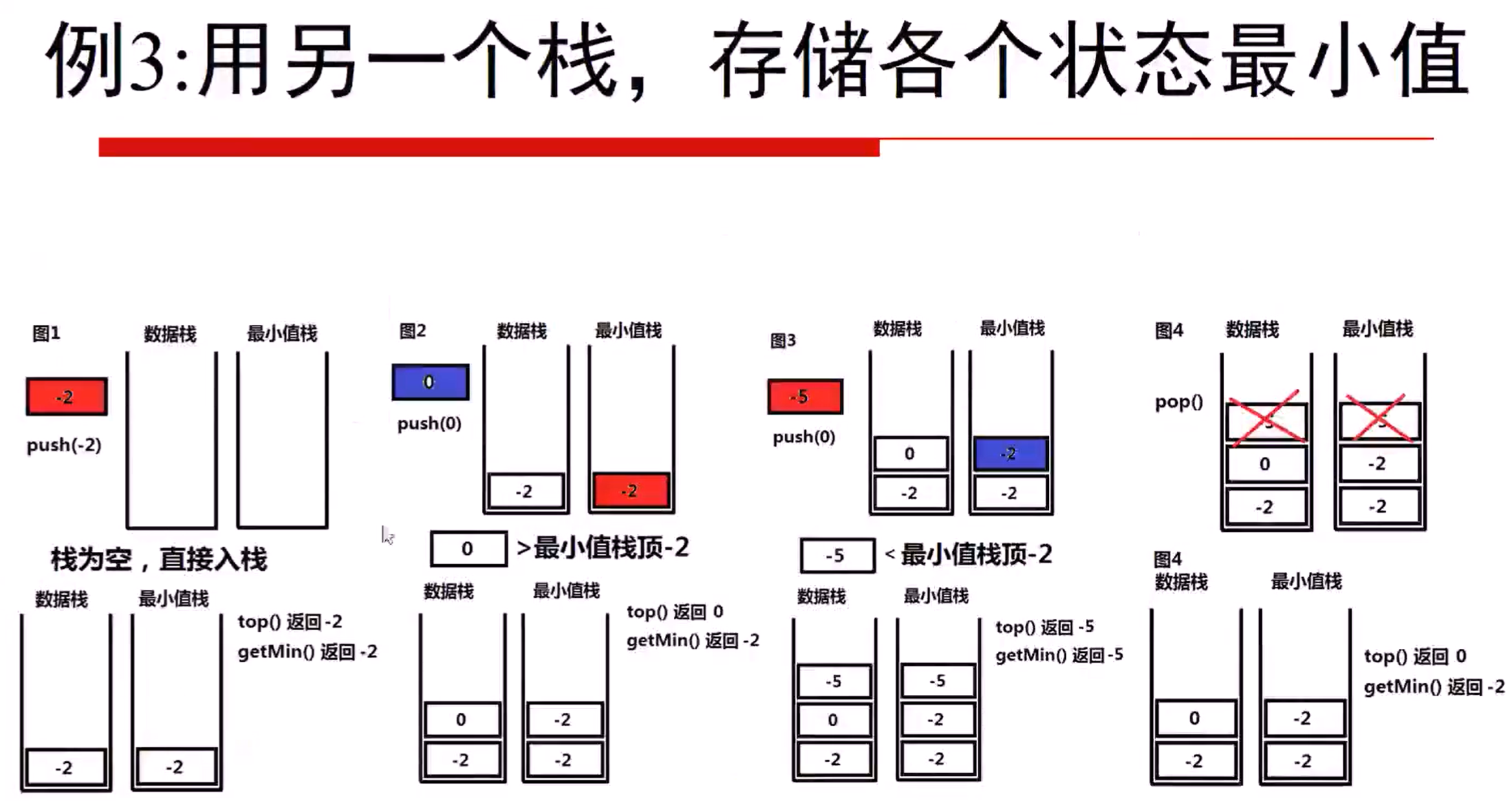
设计算法复杂度为O(1)的栈

创建一个最小值栈，存储各个状态的最小值

class MinStack
{
private:
    stack<int> S;
    stack<int> min_S;

public:
    /** initialize your data structure here. */
    MinStack()
    {
    }

    void push(int x)
    {
        S.push(x);

        if (min_S.empty())
        {
            min_S.push(x);
        }
        else
        {
            int min = min_S.top();
            if (x < min)
            {
                min = x;
            }

            min_S.push(min);
        }
    }

    void pop()
    {
        S.pop();
        min_S.pop();
    }

    int top()
    {
        return S.top();
    }

    //返回栈内最小元素
    //最关键是getMin方法达到O(1)
    int getMin()
    {
        return min_S.top();
    }
};

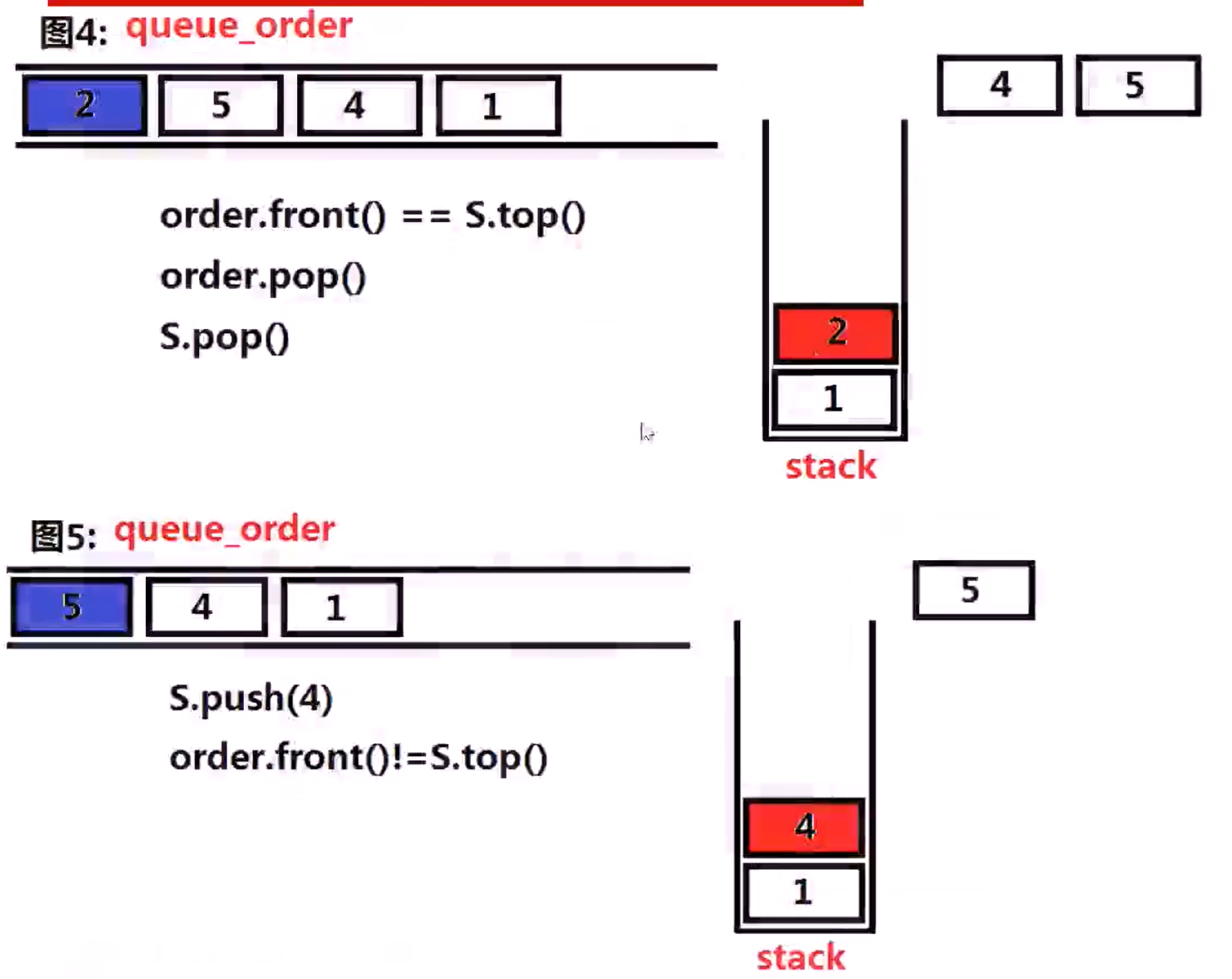
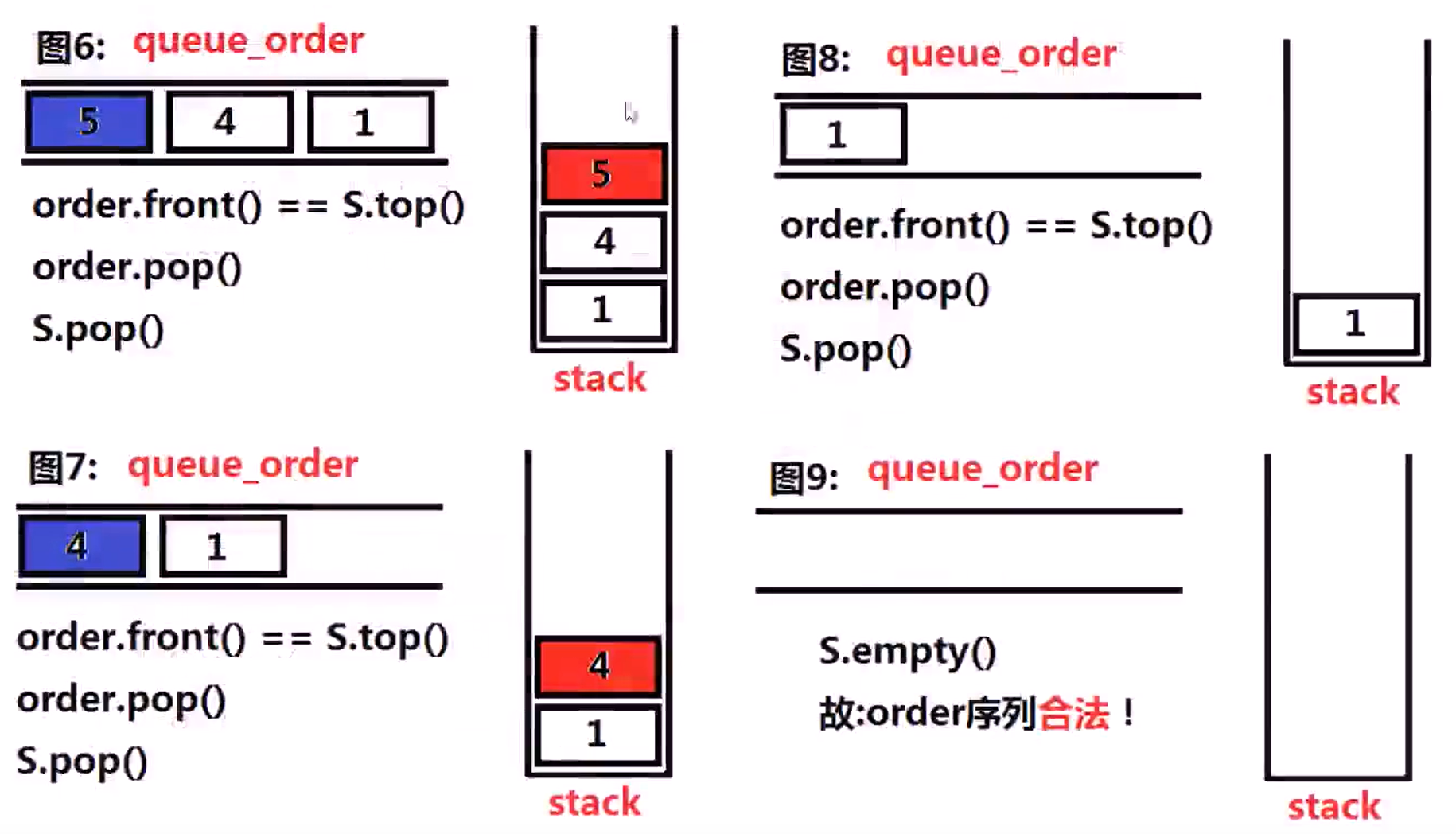
Leetcode 946 (Medium)

验证栈序列 （Leetcode 946）给定 pushed 和 popped 两个序列，每个序列中的值都不重复，只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时，返回 true；否则，返回 false 。

class Solution {
    public boolean validateStackSequences(int[] pushed, int[] popped) {
        if (pushed.length != popped.length) {
            return false;
        }

        Stack<Integer> S = new Stack();
        int index = 0;
        for (int i = 0; i < pushed.length; i++) {
            S.push(pushed[i]);
            while (!S.empty() && S.peek() == popped[index]) {
                S.pop();
                index++;
            }
        }
        return S.empty();
    }
}

class Solution
{
public:
    bool validateStackSequences(vector<int> &pushed, vector<int> &popped)
    {
        if (pushed.size() != popped.size())
        {
            return false;
        }

        int index = 0;
        stack<int> S;
        for (int i = 0; i < pushed.size(); i++)
        {
            S.push(pushed[i]);
            while (!S.empty() && S.top() == popped[index])
            {
                S.pop();
                index++;
            }
        }
        return S.empty();
    }
};

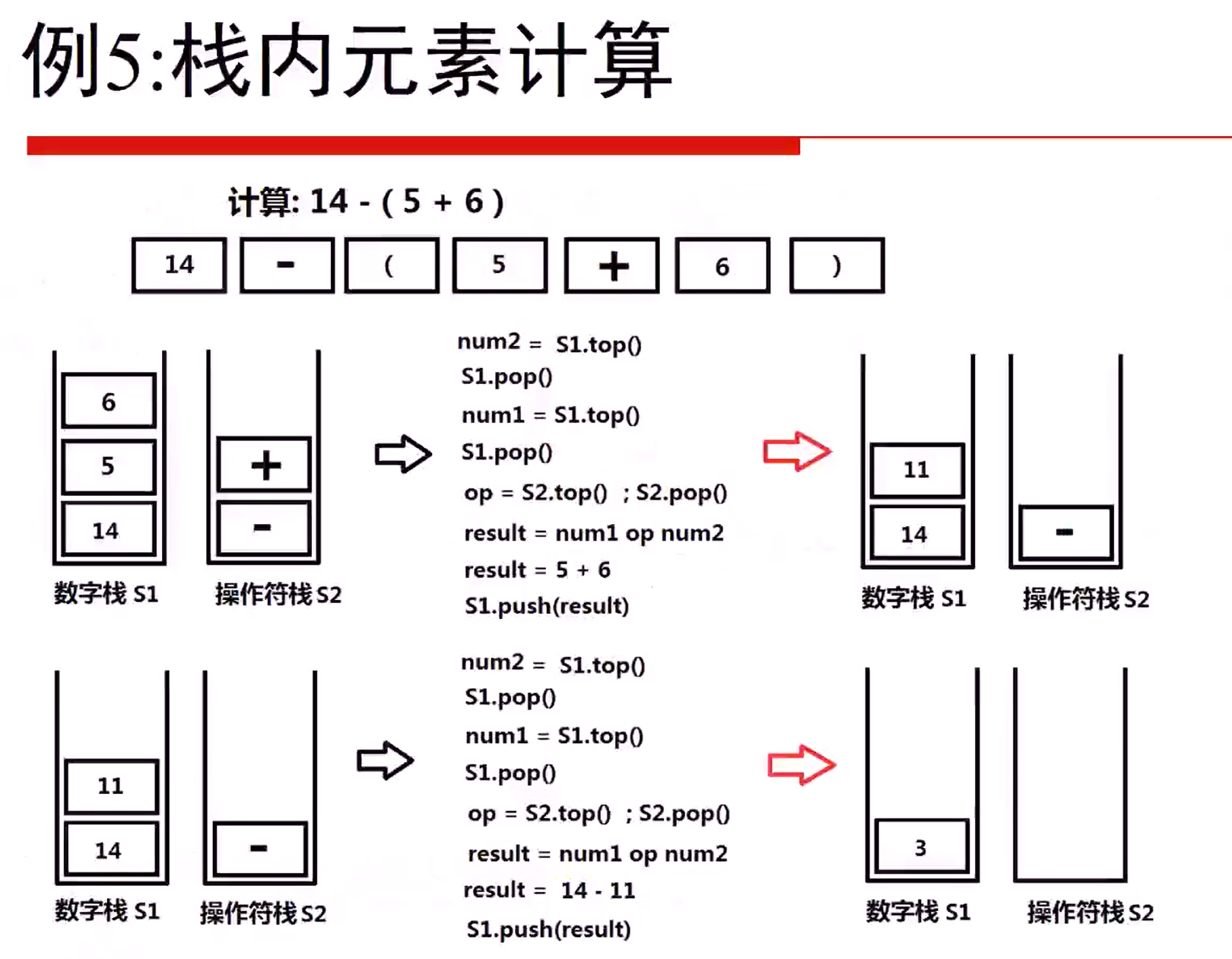
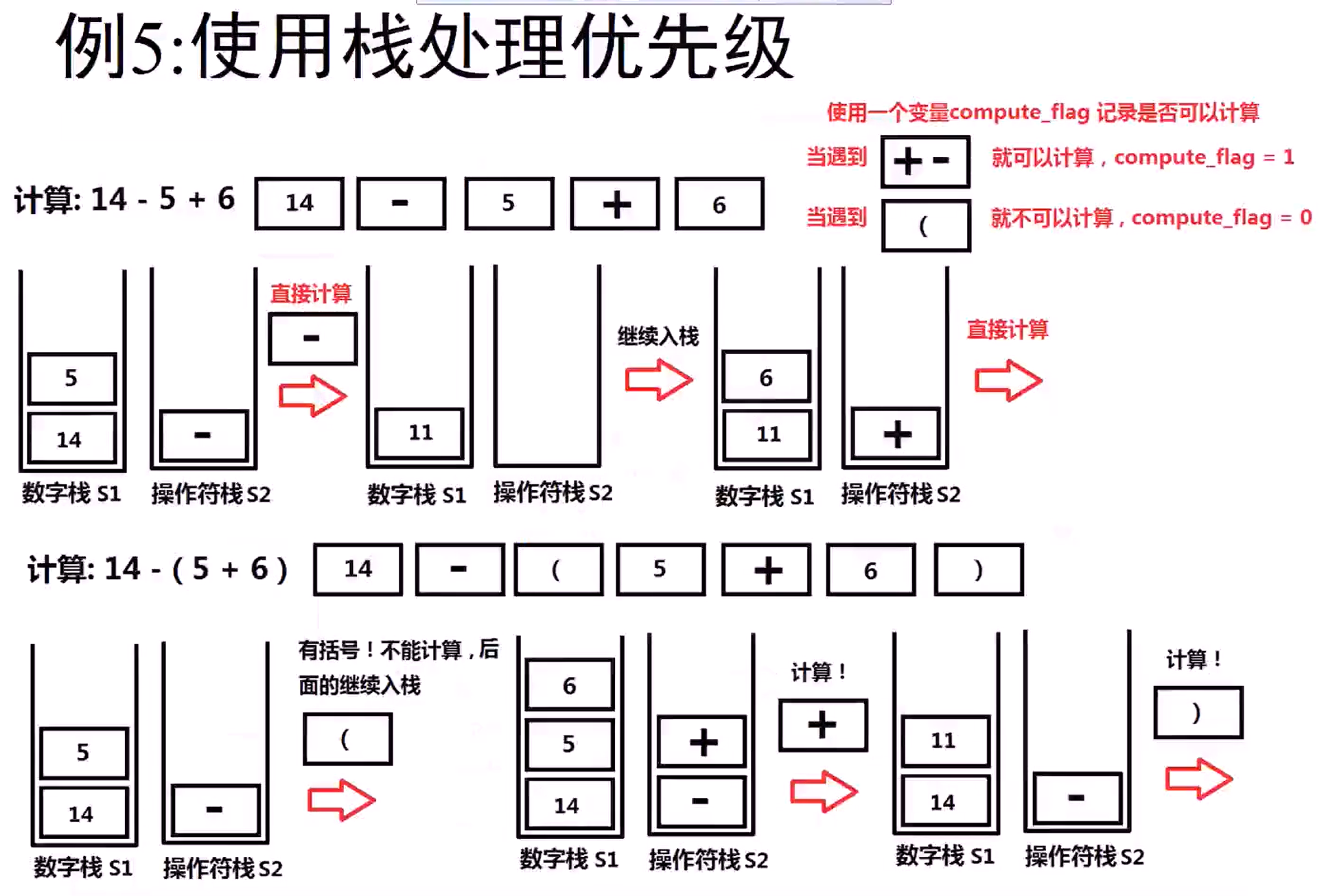
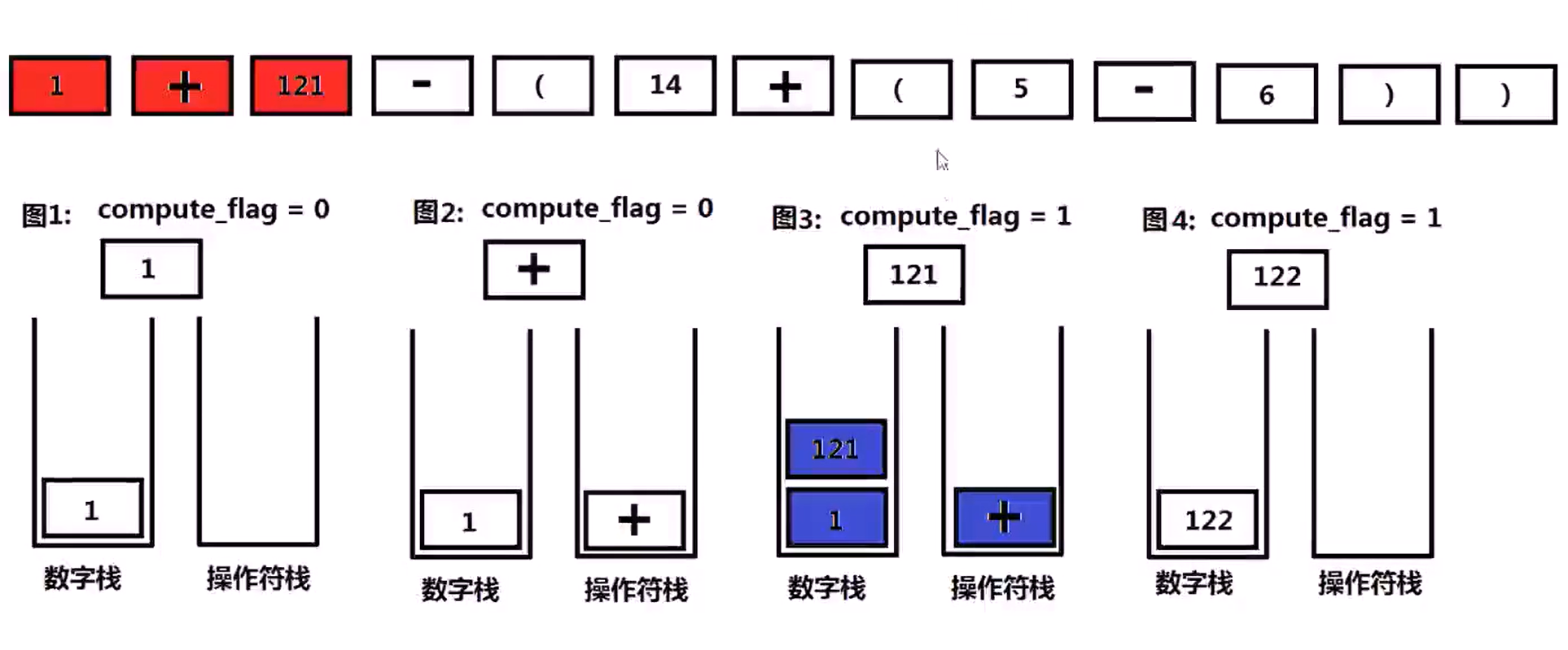
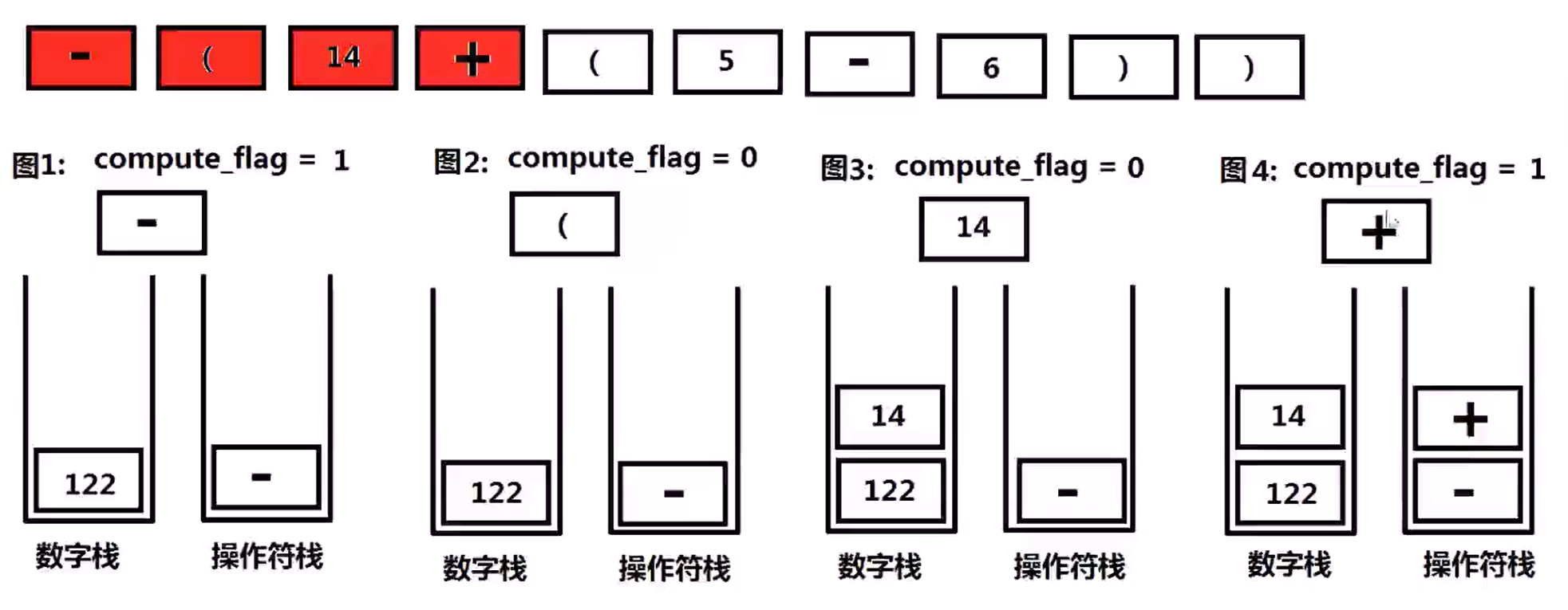
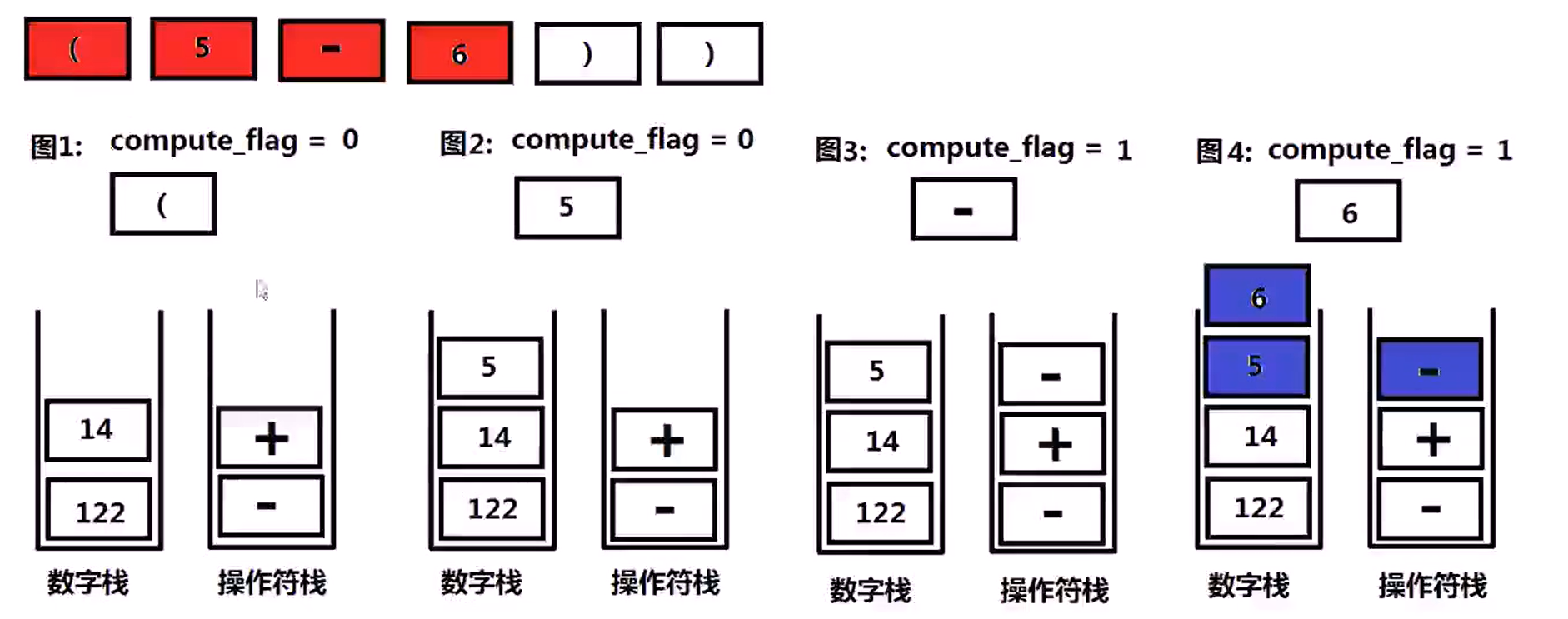
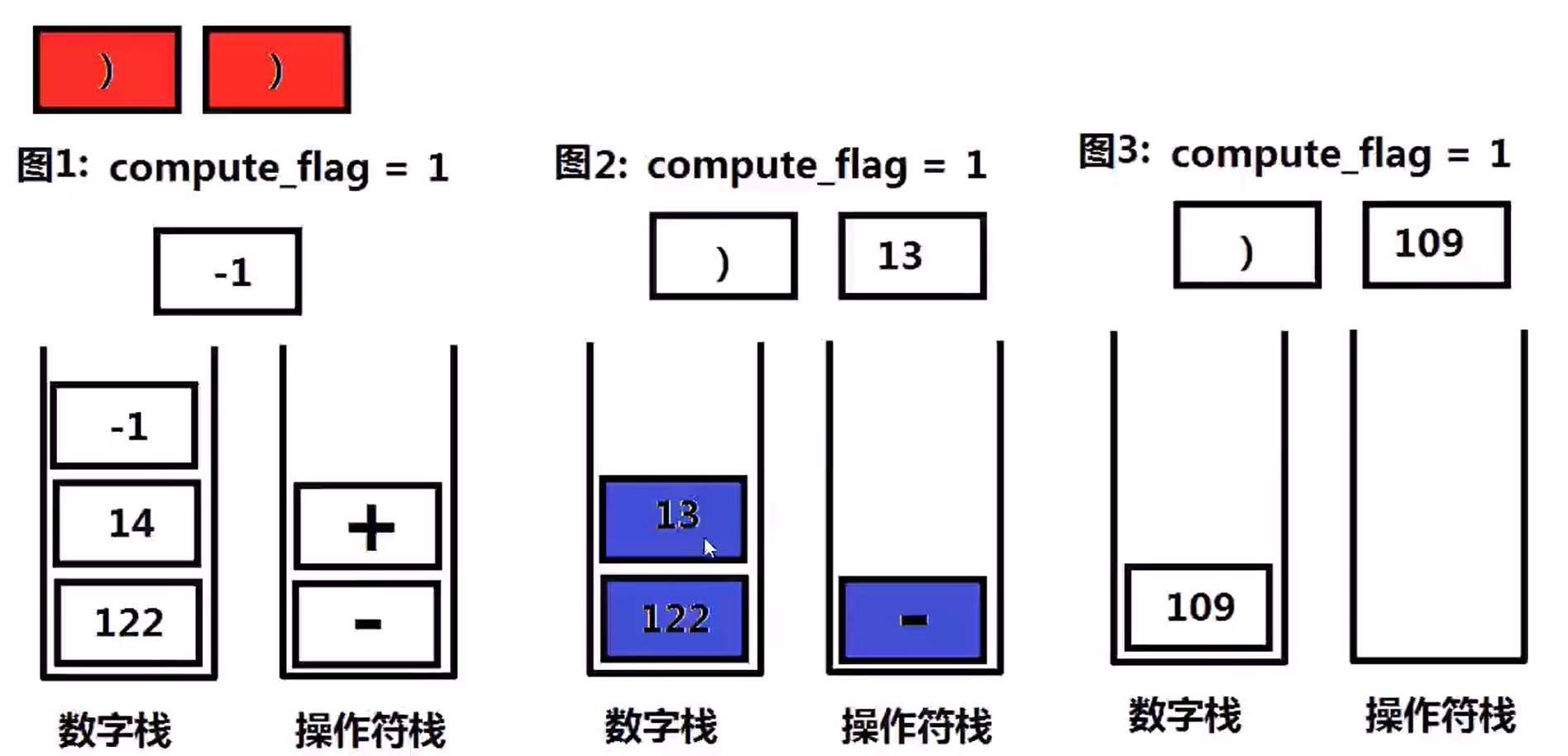
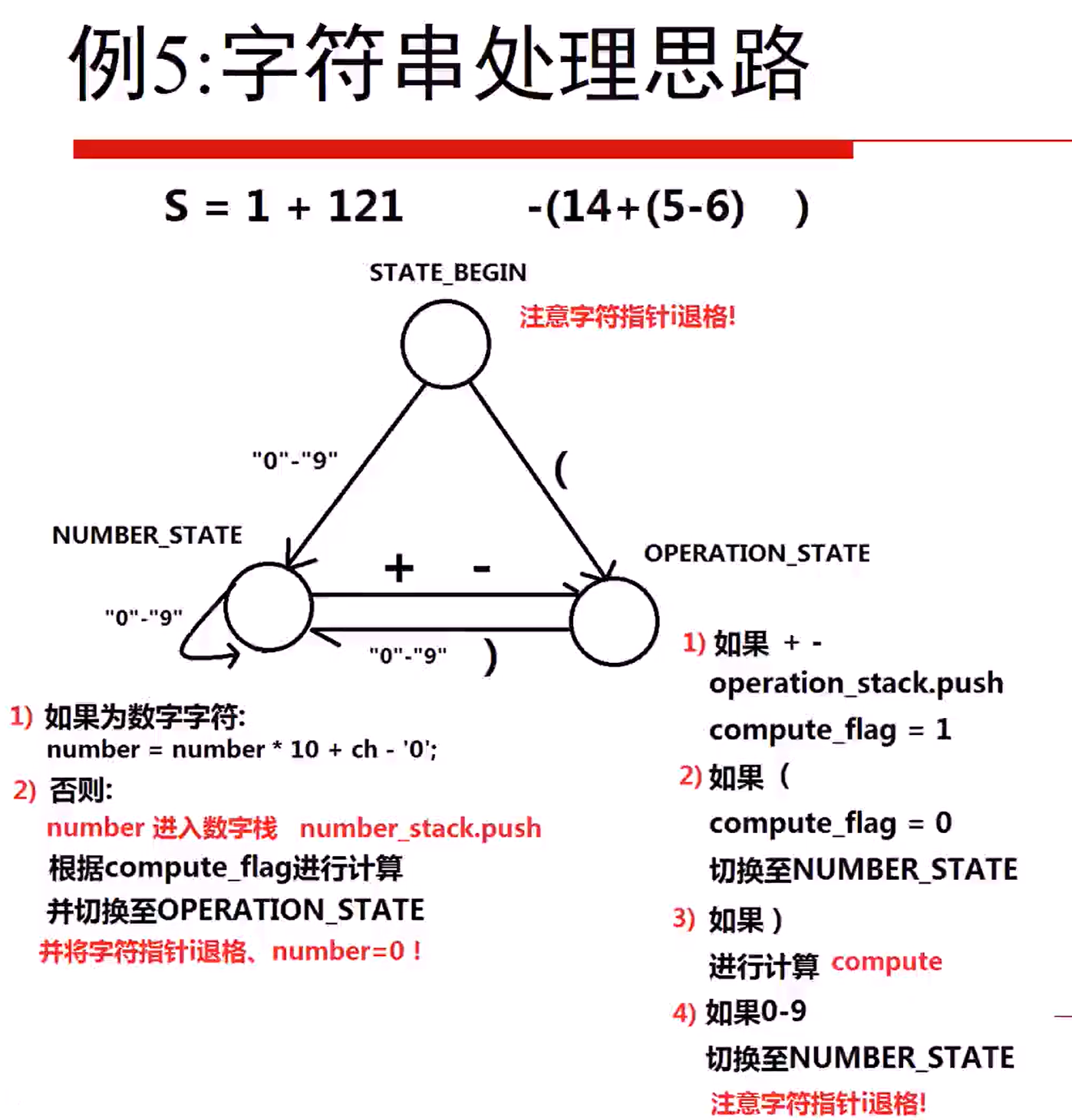
224 简单计算器(Hard)

Implement a basic calculator to evaluate a simple expression string

The expression string may contain open( and closing parenthess ), the plus + or minus sign - , non-negative integers and empty space .

设计一个计算器，输入一个字符串存储的数学表达式，可以计算包括 ( ) + - 四种符号的数学表达式，输入的数学表达式字符串保证是合法的。输入的数学表达式中可能存在空格字符

class Solution
{
public:
    /*
        计算函数
    */
    void compute(stack<int> &number_stack, stack<char> &operation_stack)
    {
        if (number_stack.size() < 2)
        {
            return;
        }

        int num2 = number_stack.top();
        number_stack.pop();
        int num1 = number_stack.top();
        number_stack.pop();

        if (operation_stack.top() == '+')
        {
            number_stack.push(num1 + num2);
        }
        else if (operation_stack.top() == '-')
        {
            number_stack.push(num1 - num2);
        }
        operation_stack.pop();
    }

    int calculate(string s)
    {
        static const int STATE_BEGIN = 0;
        static const int NUMBER_STATE = 1;
        static const int OPERATION_STATE = 2;
        stack<int> number_stack;
        stack<char> operation_stack;
        int number = 0;
        int STATE = STATE_BEGIN;
        int compute_flag = 0;

        for (int i = 0; i < s.size(); i++)
        {
            if (s[i] == ' ')
            {
                //1.
                continue;
            }
            switch (STATE)
            {
            case STATE_BEGIN:
                if (s[i] >= '0' && s[i] <= '9')
                {
                    STATE = NUMBER_STATE;
                }
                else
                {
                    STATE = OPERATION_STATE;
                }
                //2
                i--;
                break;

            case NUMBER_STATE:
                if (s[i] >= '0' && s[i] <= '9')
                {
                    number = number * 10 + (s[i] - '0');
                }
                else
                {
                    //3 number进入数字栈
                    number_stack.push(number);

                    if (compute_flag == 1)
                    {
                        compute(number_stack, operation_stack);
                    }
                    number = 0;
                    i--;
                    STATE = OPERATION_STATE;
                }
                break;

            case OPERATION_STATE:
                if (s[i] == '+' || s[i] == '-')
                {
                    operation_stack.push(s[i]);
                    //4
                    compute_flag = 1;
                }
                else if (s[i] == '(')
                {
                    //5
                    STATE = NUMBER_STATE;

                    compute_flag = 0;
                }
                else if (s[i] >= '0' && s[i] <= '9')
                {
                    STATE = NUMBER_STATE;
                    i--;
                }
                else if (s[i] == ')')
                {
                    compute(number_stack, operation_stack);
                }
                break;
            }
        }

        if (number != 0)
        {
            number_stack.push(number);
            compute(number_stack, operation_stack);
        }
        if (number == 0 && number_stack.empty())
        {
            return 0;
        }
        return number_stack.top();
    }

    /*
        将字符串转换为对应整数
    */
    int parse_string(string str)
    {
        int number = 0;
        for (int i = 0; i < str.length(); i++)
        {
            number = number * 10 + str[i] - '0';
        }
        return number;
    }
};

二叉堆属性

最（大）小二叉堆，最（大）小值先出的完全二叉树

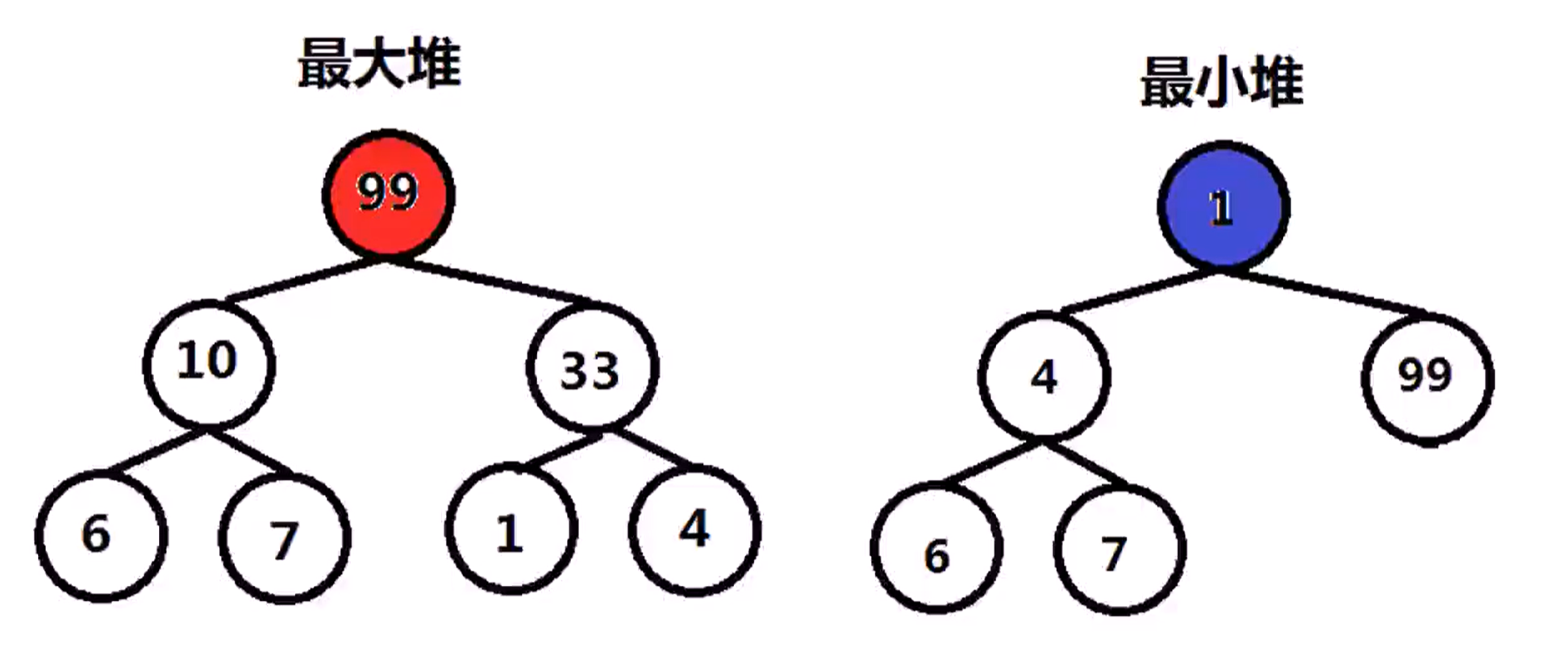
logn复杂度，堆顶为最（大）小数，字数也满足同样的性质

STL优先级队列（二叉堆）

二叉堆，最小（大）值先出的完全二叉树

#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>

using namespace std;

/*
    在优先队列中，元素被赋予优先级。当访问元素时，
    具有最高优先级的元素最先删除。优先队列具有最高级先出
     （first in, largest out）的行为特征。
*/
int main()
{
    priority_queue<int> big_heap;                              //默认构造是最大堆
    priority_queue<int, vector<int>, greater<int>> small_heap; //构造最小堆
    priority_queue<int, vector<int>, less<int>> big_heap2;     //最大堆的特殊构造方法

    if (big_heap.empty())
    {
        printf("big_heap is empty ! \n");
    }
    int test[] = {6, 10, 1, 7, 99, 4, 33};
    for (int i = 0; i < 7; i++)
    {
        big_heap.push(test[i]);
    }
    printf("big_heap.top = %d \n", big_heap.top());
    //1.
    big_heap.push(1000);

    printf("big_heap.top = %d \n", big_heap.top());

    for (int i = 0; i < 3; i++)
    {
        //3
        big_heap.pop();
    }

    printf("big_heap.top = %d \n", big_heap.top());
    printf("big_heap.size = %d \n", big_heap.size());

    return 0;
}

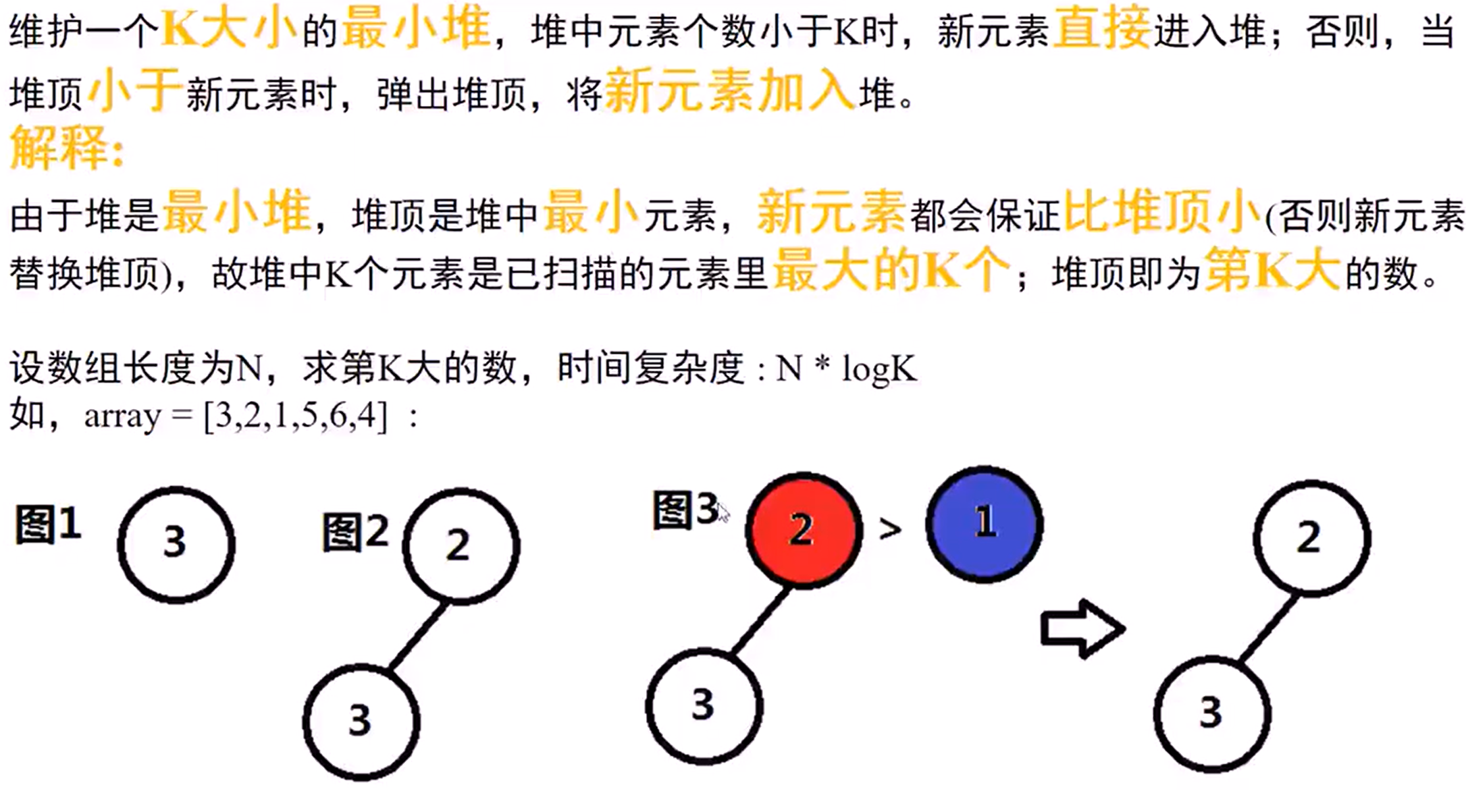
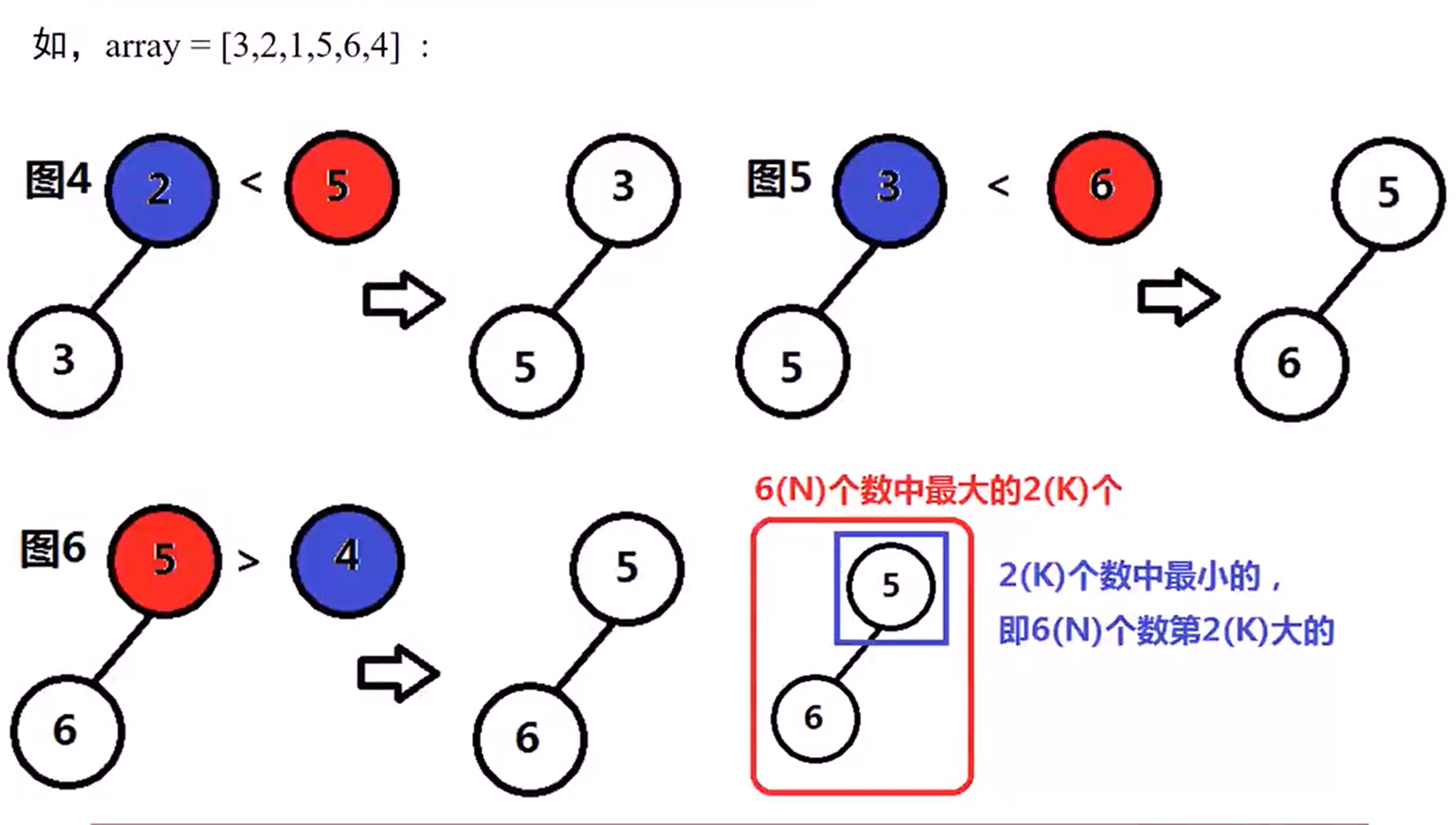
215 Kth Larget Element in an Array(Easy)

已知一个未排序的数组，求这个数组中第K大的数字

最大堆暴力解法：

class Solution
{
public:
    int findKthLargest(vector<int> &nums, int k)
    {
        priority_queue<int> Q;
        for (int i = 0; i < nums.size(); i++)
        {
            Q.push(nums[i]);
        }

        for (int i = 0; i < k - 1; i++)
        {
            Q.pop();
        }
        return Q.top();
    }
};

int main()
{

    vector<int> vec = {3, 2, 1, 5, 6, 4};
    int k = 2;

    Solution solve;
    int result = solve.findKthLargest(vec, k);
    cout << result;

    return 0;
}

最小堆解法

#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>

using namespace std;

class Solution
{
public:
    int findKthLargest(vector<int> &nums, int k)
    {
        priority_queue<int, vector<int>, greater<int>> Q; //最小堆
        for (int i = 0; i < nums.size(); i++)
        {
            if (/*1*/ Q.size() < k)
            {
                Q.push(nums[i]);
            }
            else if (/*2*/ Q.top() < nums[i])
            {
                Q.pop();
                //3
                Q.push(nums[i]);
            }
        }
        return Q.top();
    }
};

int main()
{

    vector<int> vec = {3, 2, 1, 5, 6, 4};
    int k = 3;

    Solution solve;
    int result = solve.findKthLargest(vec, k);
    cout << result;

    return 0;
}

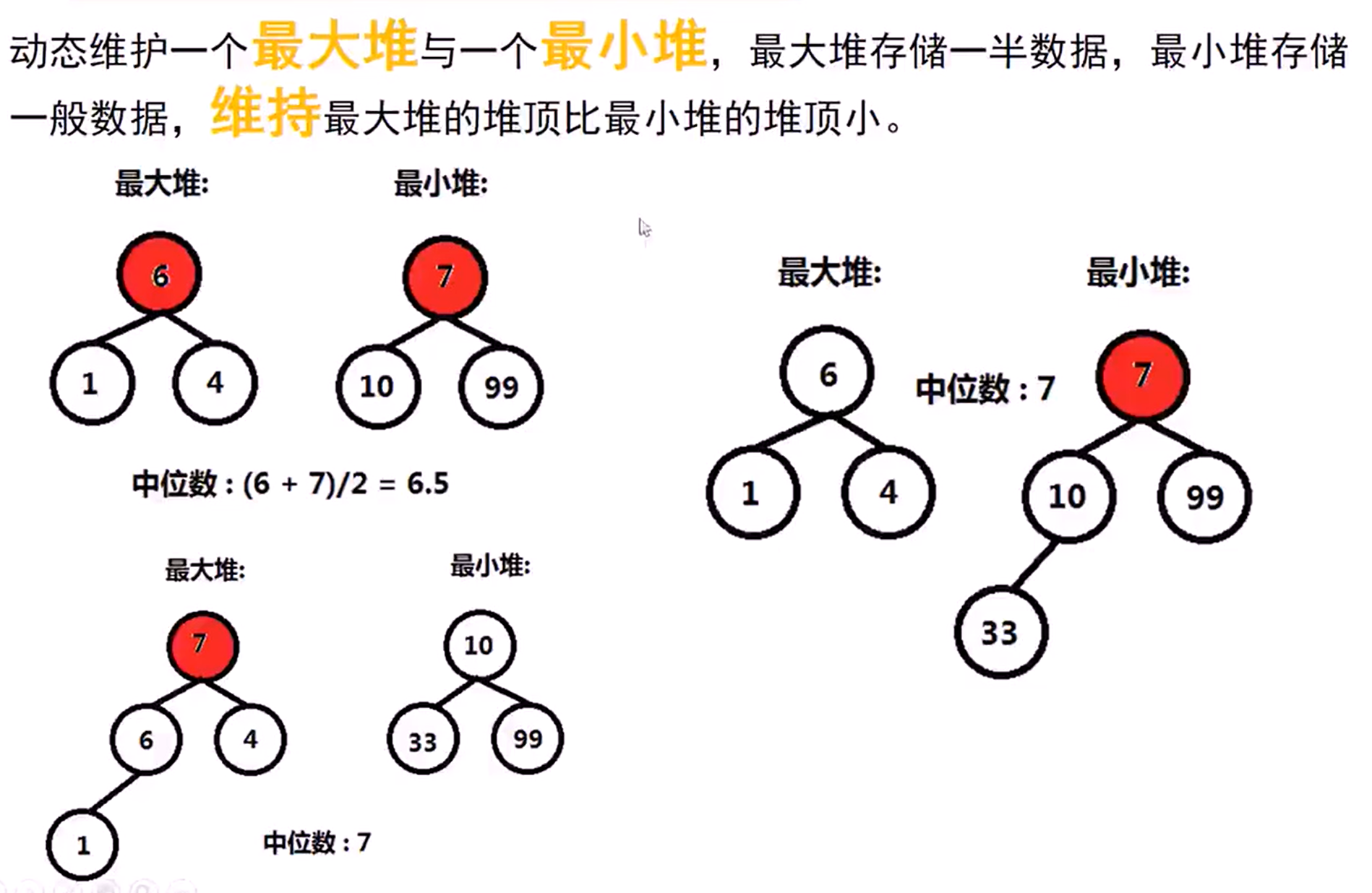
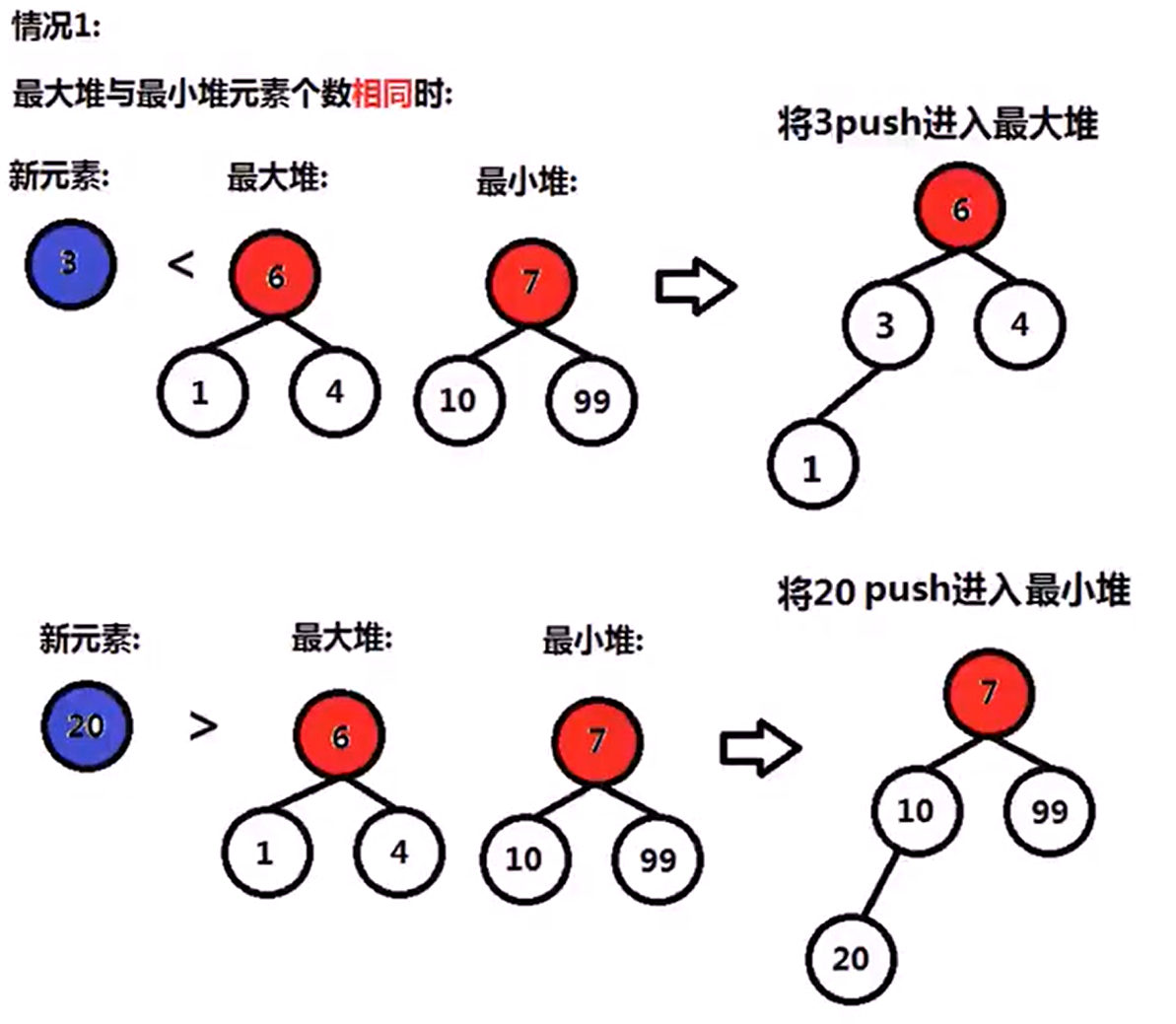
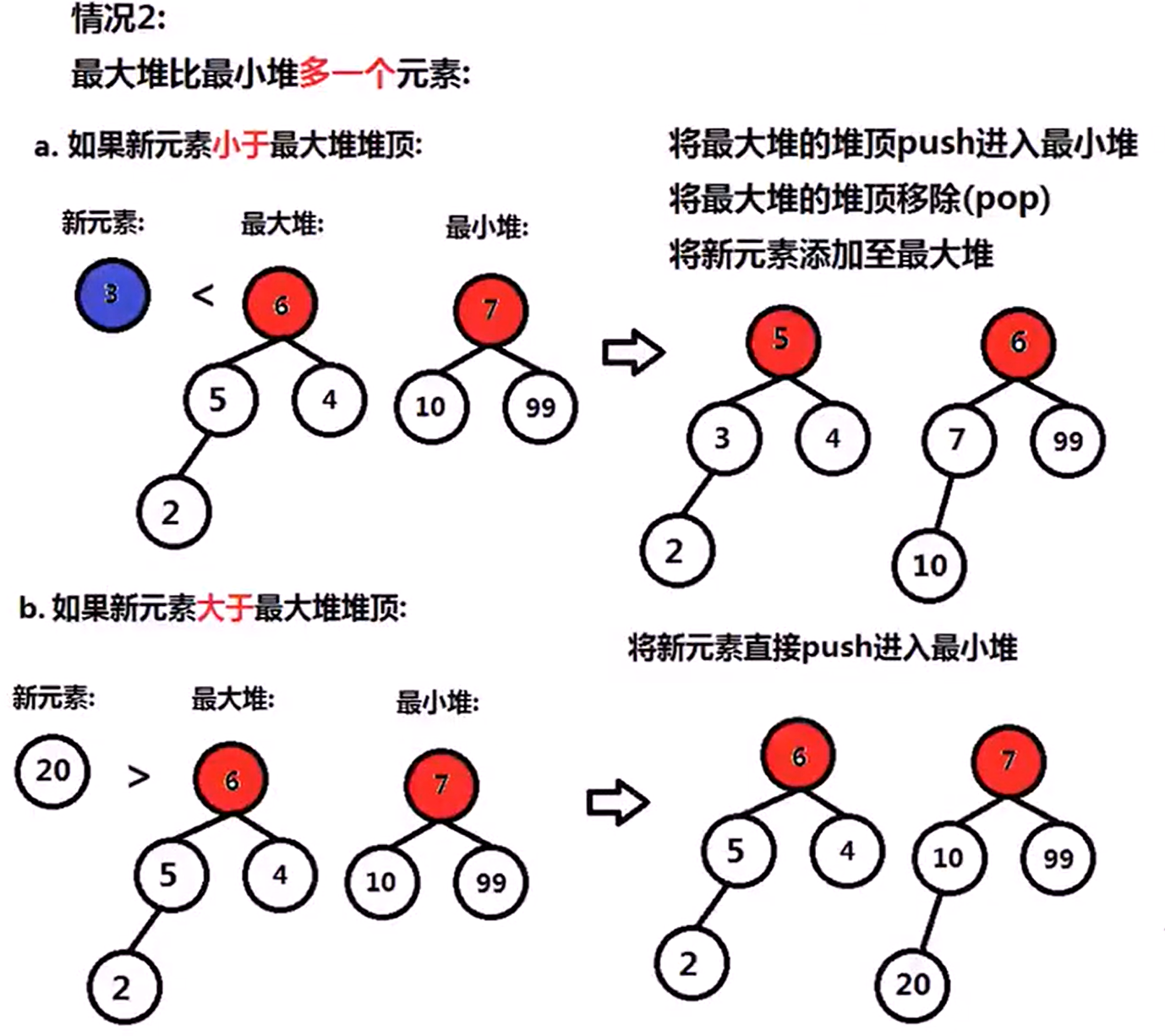
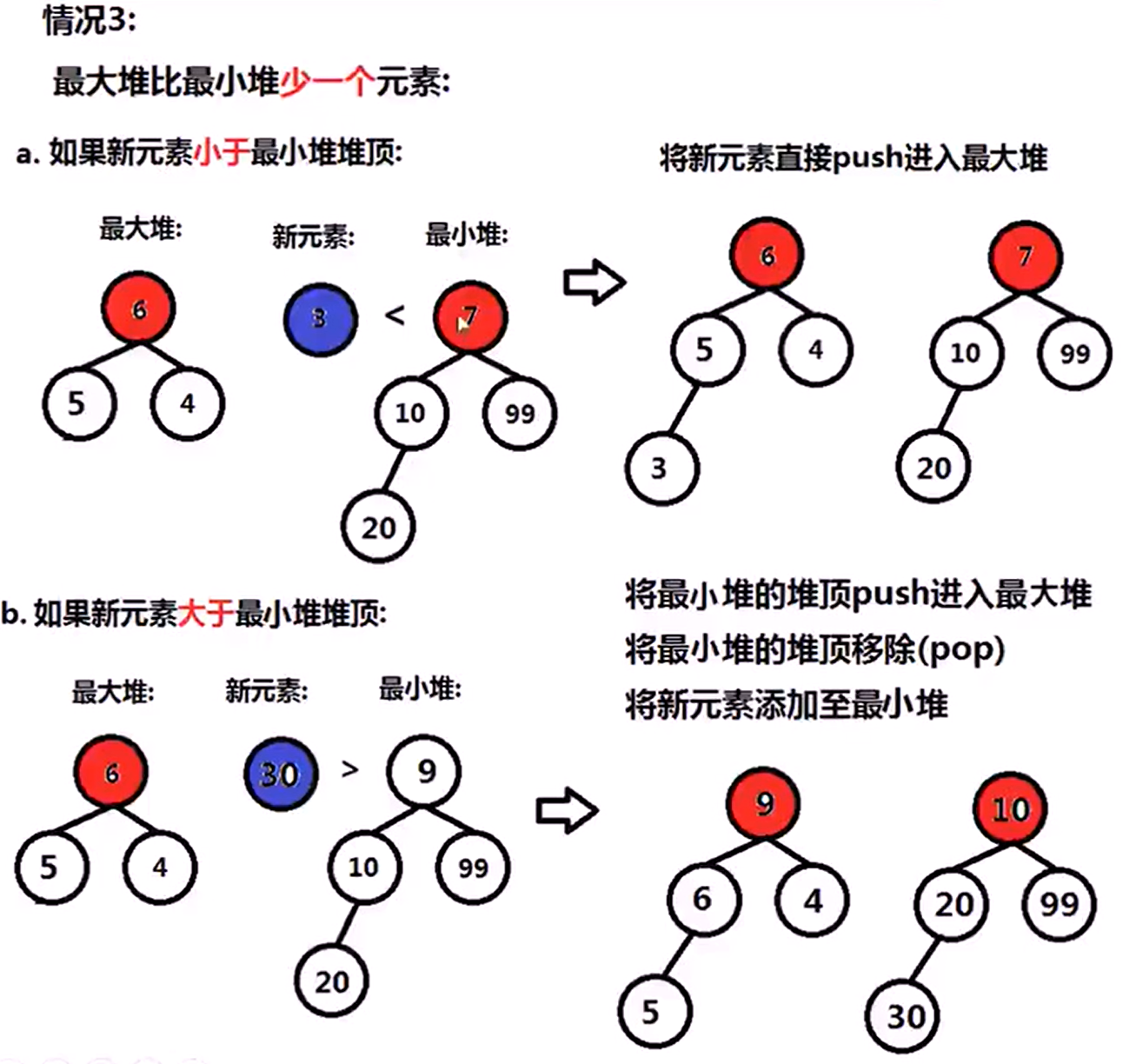
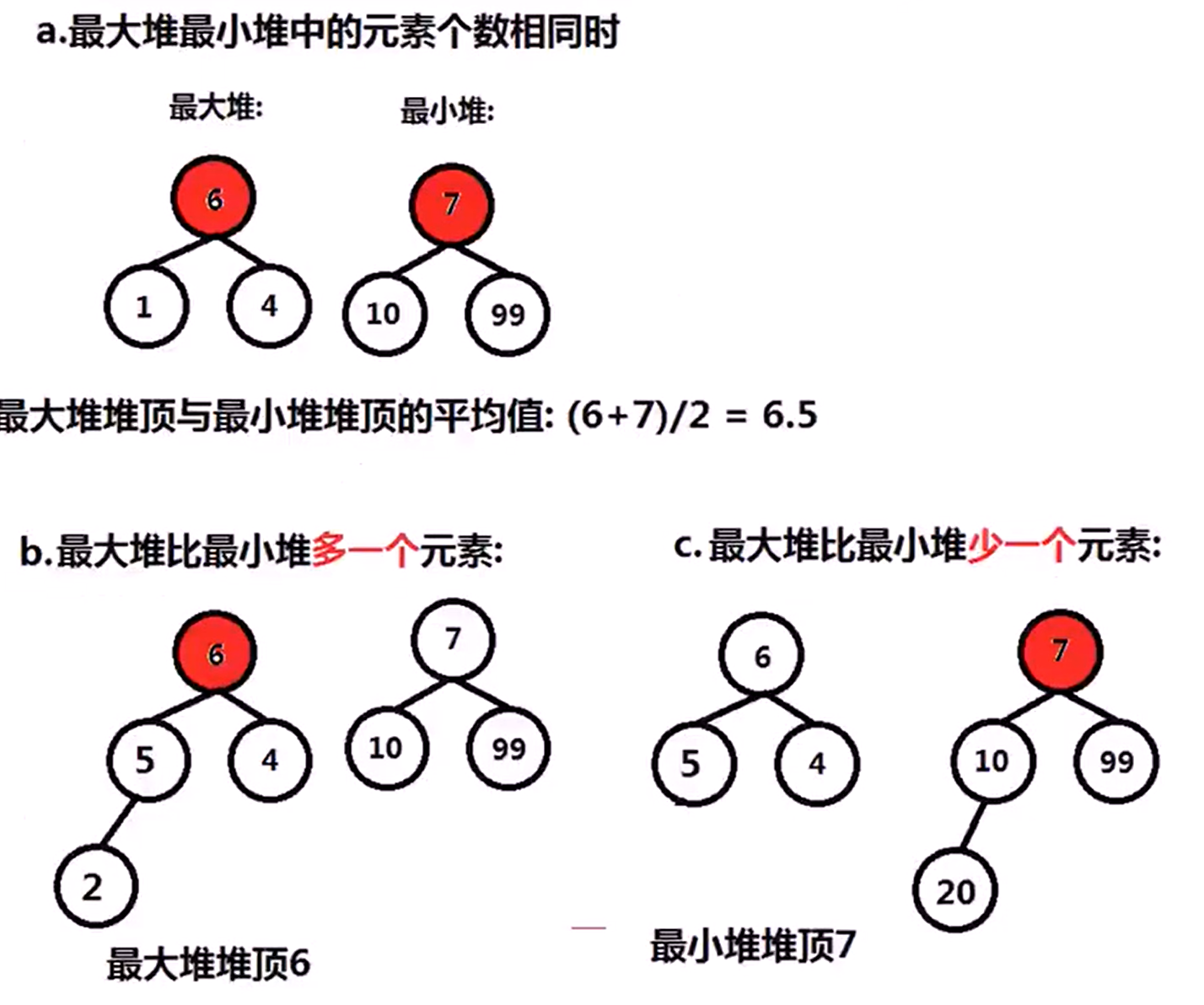
295 Find Median From Data Stream(Hard)

Median is the middle value in an ordered integer list. if the size of the list is even , there is no middle value. So the median is the mean of the tweo middle value.

Design a data structure that supports the following two operations:

void addNum(int num) -> Add a integer number from the data stream to the data structure
double findMedian() -> Return the median of all elements so far.

直观法

#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>

using namespace std;

class MedianFinder
{
private:
    priority_queue<int> big_queue;
    priority_queue<int, vector<int>, greater<int>> small_queue;

public:
    /** initialize your data structure here. */
    MedianFinder()
    {
    }

    void addNum(int num) // 向数据结构中添加一个整数
    {
        if (big_queue.empty())
        {
            big_queue.push(num);
            return;
        }
        if (big_queue.size() == small_queue.size())
        {
            if (/* 1 */ num < big_queue.top())
            {
                big_queue.push(num);
            }
            else
            {
                small_queue.push(num);
            }
        }
        else if (/*2*/ big_queue.size() == small_queue.size() + 1)
        {
            if (num > big_queue.top())
            {
                small_queue.push(num);
            }
            else
            {
                //3
                small_queue.push(big_queue.top());

                big_queue.pop();
                big_queue.push(num);
            }
        }
        else if (/*4*/ big_queue.size() + 1 == small_queue.size())
        {
            if (/*5*/ num < small_queue.top())
            {
                big_queue.push(num);
            }
            else
            {
                big_queue.push(small_queue.top());
                small_queue.pop();
                small_queue.push(num);
            }
        }
    }

    double findMedian() //返回该数据结构中维护的数据的中位数
    {
        if (big_queue.size() == small_queue.size())
        {
            return (big_queue.top() + small_queue.top()) / 2.0;
        }
        else if (big_queue.size() == small_queue.size() + 1)
        {
            return big_queue.top();
        }
        else
        {
            return small_queue.top();
        }
    }
};

int main()
{
    MedianFinder M;
    M.addNum(2);
    M.addNum(1);

    printf("%lf\n", M.findMedian()); //1.5

    M.addNum(4);

    printf("%lf\n", M.findMedian()); //2

    M.addNum(3);

    printf("%lf\n", M.findMedian()); //2.5

    return 0;
}

//Java Code
public class MedianFinder {
    private PriorityQueue<Integer> smallQueue = new PriorityQueue<>();
    private PriorityQueue<Integer> bigQueue = new PriorityQueue<>((o1, o2) -> o2 - o1);

    /**
     * initialize your data structure here.
     */
    public MedianFinder() {

    }

    public void addNum(int num) {
        if (bigQueue.isEmpty()) {
            bigQueue.add(num);
            return;
        }
        if (bigQueue.size() == smallQueue.size()) {
            if (num < bigQueue.peek()) {
                bigQueue.add(num);
            } else {
                smallQueue.add(num);
            }
        } else if (bigQueue.size() == smallQueue.size() + 1) {
            if (num > bigQueue.peek()) {
                smallQueue.add(num);
            } else {
                smallQueue.add(bigQueue.poll());
                bigQueue.add(num);
            }
        } else if (bigQueue.size() + 1 == smallQueue.size()) {
            if (num < smallQueue.peek()) {
                bigQueue.add(num);
            } else {
                bigQueue.add(smallQueue.poll());
                smallQueue.add(num);
            }
        }
    }

    public double findMedian() {
        if (bigQueue.size() == smallQueue.size()) {
            return (bigQueue.peek() + smallQueue.peek()) / 2.0;
        } else if (bigQueue.size() == smallQueue.size() + 1) {
            return bigQueue.peek();
        } else {
            return smallQueue.peek();
        }
    }
}


class Test {
    public static void main(String[] args) {
        MedianFinder medianFinder = new MedianFinder();
        medianFinder.addNum(2);
        medianFinder.addNum(1);

        System.out.println(medianFinder.findMedian());

        medianFinder.addNum(4);

        System.out.format("%.2f\n", medianFinder.findMedian());

        medianFinder.addNum(3);

        System.out.format("%.2f\n", medianFinder.findMedian());

    }
}

预备知识——栈与队列#

栈#

队列#

255 Implement Stack using Queues (Easy)#

232 Implement Queue using Stacks (Easy)#

155 Min Stack (Easy)#

Leetcode 946 (Medium)#

224 简单计算器(Hard)#

二叉堆属性#

STL优先级队列（二叉堆）#

215 Kth Larget Element in an Array(Easy)#

295 Find Median From Data Stream(Hard)#