LeetCode树与图

March 14, 2020 · 6 min read

Ban

ChangAn University

二叉树

二叉树基础

二叉树前序遍历

#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>

using namespace std;

struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

/*
    前序遍历
*/
void preorder_print(TreeNode *node, int layer)
{
    if (!node)
    {
        return;
    }

    for (int i = 0; i < layer; i++)
    {
        printf("-----");
    }
    printf("[%d]\n", node->val);
    preorder_print(node->left, layer + 1);
    preorder_print(node->right, layer + 1);
}

int main()
{

    TreeNode a(1);
    TreeNode b(2);
    TreeNode c(5);
    TreeNode d(3);
    TreeNode e(4);
    TreeNode f(6);

    a.left = &b;
    a.right = &c;
    b.left = &d;
    b.right = &e;
    c.right = &f;

    preorder_print(&a, 0);

    return 0;
}

//java code
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        this.val = val;
    }
}


class Test {
    public static void preorderPrint(TreeNode node, int layer) {
        if (node == null) {
            return;
        }
        for (int i = 0; i < layer; i++) {
            System.out.print("-----");
        }
        System.out.format("[%d]\n", node.val);
        preorderPrint(node.left, ++layer);
        preorderPrint(node.right, ++layer);
    }

    public static void main(String[] args) {
        TreeNode a = new TreeNode(1);
        TreeNode b = new TreeNode(2);
        TreeNode c = new TreeNode(5);
        TreeNode d = new TreeNode(3);
        TreeNode e = new TreeNode(4);
        TreeNode f = new TreeNode(6);

        a.left = b;
        a.right = c;
        b.left = d;
        b.right = e;
        c.right = f;

        preorderPrint(a, 0);
    }
}

//伪代码
//中序
preOrderPrint(node.left, ++layer);
System.out.format("[%d]\n", node.val);
preOrderPrint(node.right, ++layer);

//后序
preOrderPrint(node.left, ++layer);
preOrderPrint(node.right, ++layer);
System.out.format("[%d]\n", node.val);

113 Path Sum II(Medium)

Given a binary tree and sum, find all root-to-leaf paths where each path's sum equals the given sum

Note: A leaf is a node with no child

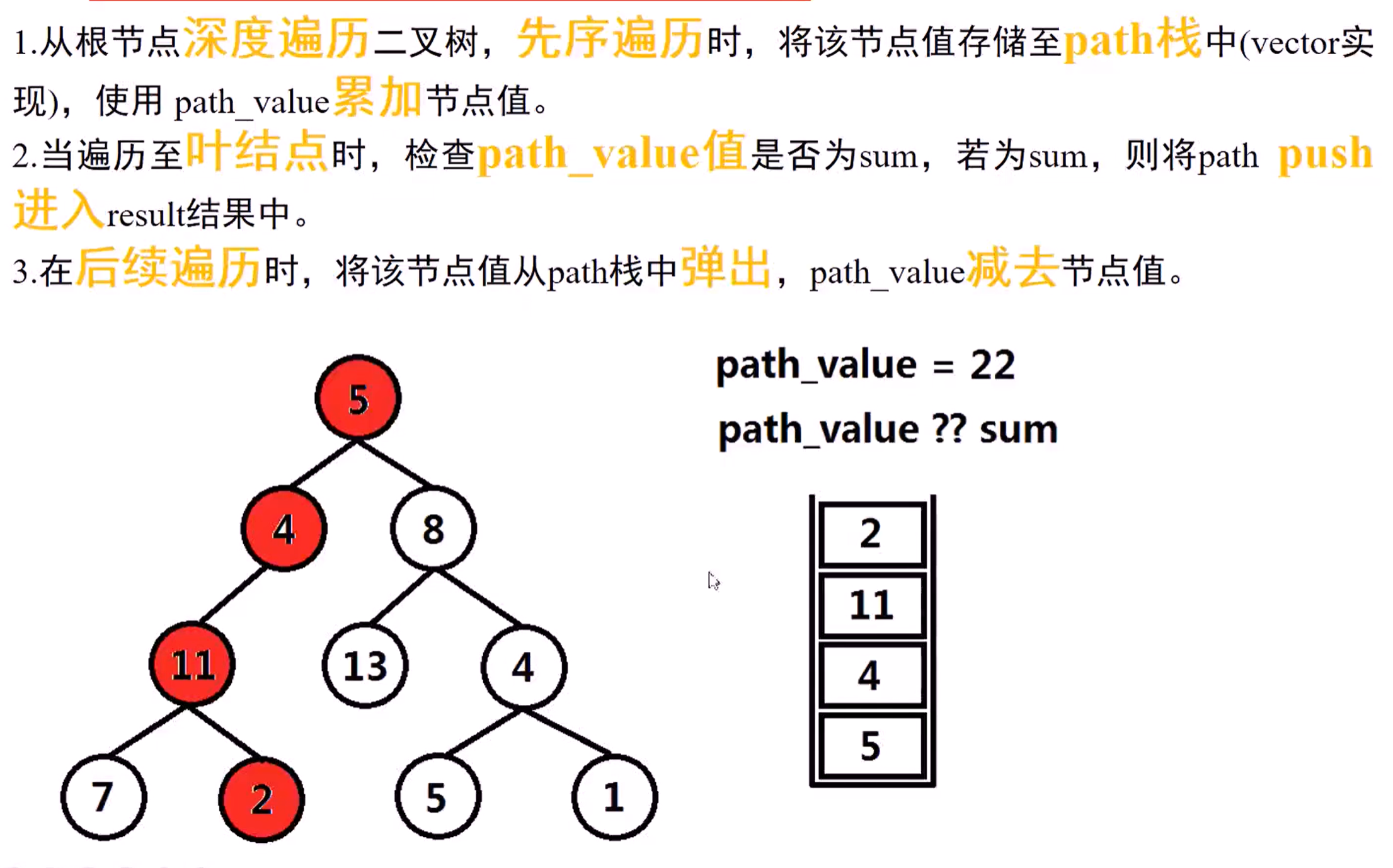
struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution
{
private:
    void preorder(TreeNode *node, int &path_value, int sum, vector<int> &path,
                  vector<vector<int>> &result)
    {
        if (!node)
        {
            return;
        }

        path_value += node->val;
        //1
        path.push_back(node->val);

        //到达叶节点
        if ((!node->left) && (!node->right) && (path_value == sum))
        {
            result.push_back(path);
        }

        preorder(node->left, path_value, sum, path, result);
        preorder(node->right, path_value, sum, path, result);

        path_value -= node->val;
        //3.遍历例完毕，将该节点从路径中弹出
        path.pop_back();
    }

public:
    vector<vector<int>> pathSum(TreeNode *root, int sum)
    {
        vector<vector<int>> result;
        vector<int> path;
        int path_value = 0;
        preorder(root, path_value, sum, path, result);
        return result;
    }
};

int main()
{

    TreeNode a(5);
    TreeNode b(4);
    TreeNode c(8);
    TreeNode d(11);
    TreeNode e(13);
    TreeNode f(4);
    TreeNode g(7);
    TreeNode h(2);
    TreeNode i(5);
    TreeNode j(1);

    a.left = &b;
    a.right = &c;
    b.left = &d;
    d.left = &g;
    d.right = &h;
    c.left = &e;
    c.right = &f;
    f.left = &i;
    f.right = &j;

    Solution solve;

    vector<vector<int>> result = solve.pathSum(&a, 22);

    for (int i = 0; i < result.size(); i++)
    {
        for (int j = 0; j < result[i].size(); j++)
        {
            printf("[%d]", result[i][j]);
        }
        printf("\n");
    }

    system("pause");
    return 0;
}

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int val) {
        this.val = val;
    }
}


class Solution {
    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> result = new ArrayList<>();
    private int pathValue = 0;

    public List<List<Integer>> pathSum(TreeNode root, int sum) {

        if (root == null) {
            return result;
        }

        pathValue += root.val;
        path.add(root.val);

        if (root.left == null && root.right == null && pathValue == sum) {
            result.add(new ArrayList<>(path));
        }

        pathSum(root.left, sum);
        pathSum(root.right, sum);

        pathValue -= root.val;
        path.remove(path.size() - 1);

        return result;
    }
}

class Test {
    public static void main(String[] args) {
        TreeNode a = new TreeNode(5);
        TreeNode b = new TreeNode(4);
        TreeNode c = new TreeNode(8);
        TreeNode d = new TreeNode(11);
        TreeNode e = new TreeNode(13);
        TreeNode f = new TreeNode(4);
        TreeNode g = new TreeNode(7);
        TreeNode h = new TreeNode(2);
        TreeNode i = new TreeNode(5);
        TreeNode j = new TreeNode(1);

        a.left = b;
        a.right = c;
        b.left = d;
        d.left = g;
        d.right = h;
        c.left = e;
        c.right = f;
        f.left = i;
        f.right = j;

        Solution solve = new Solution();
        List<List<Integer>> result = solve.pathSum(a, 22);

        for (int k = 0; k < result.size(); k++) {
            for (int l = 0; l < result.get(k).size(); l++) {
                System.out.format("[%d]", result.get(k).get(l));
            }
            System.out.println("\n");
        }
    }
}

236 Lowest Common Ancestor of a Binary Tree(Medium)

Given a binary tree, find the lowest common ancestor(LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia :“The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

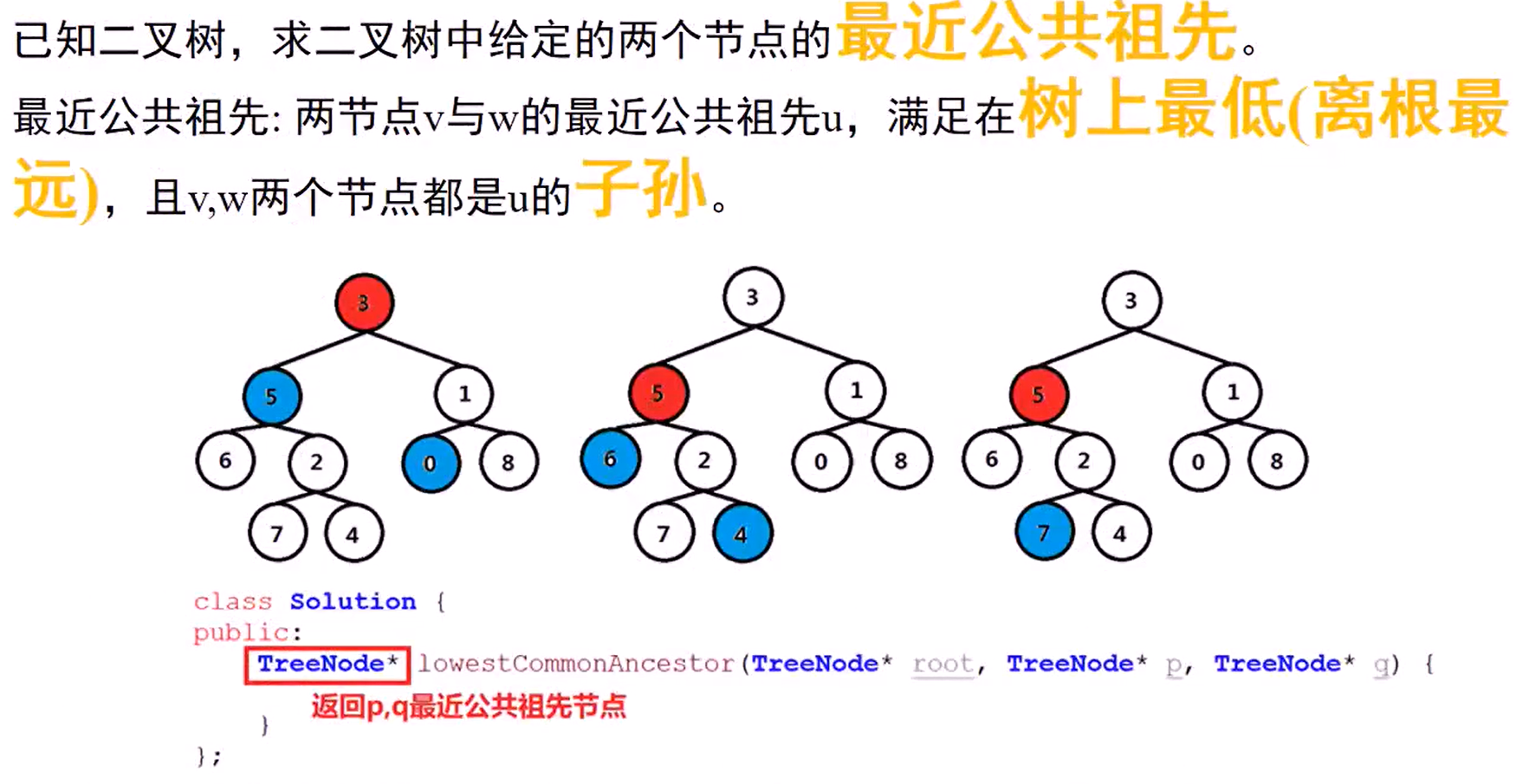
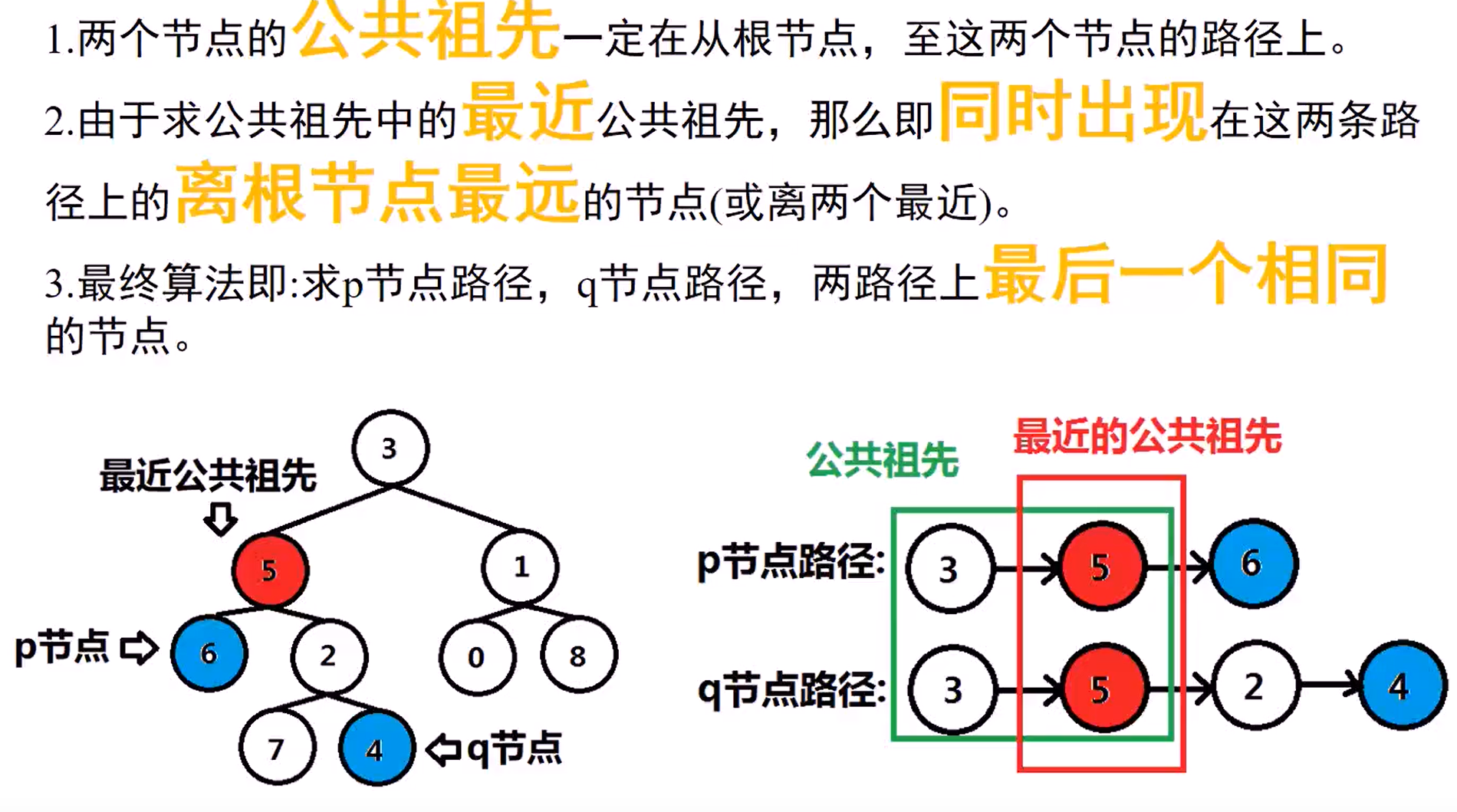
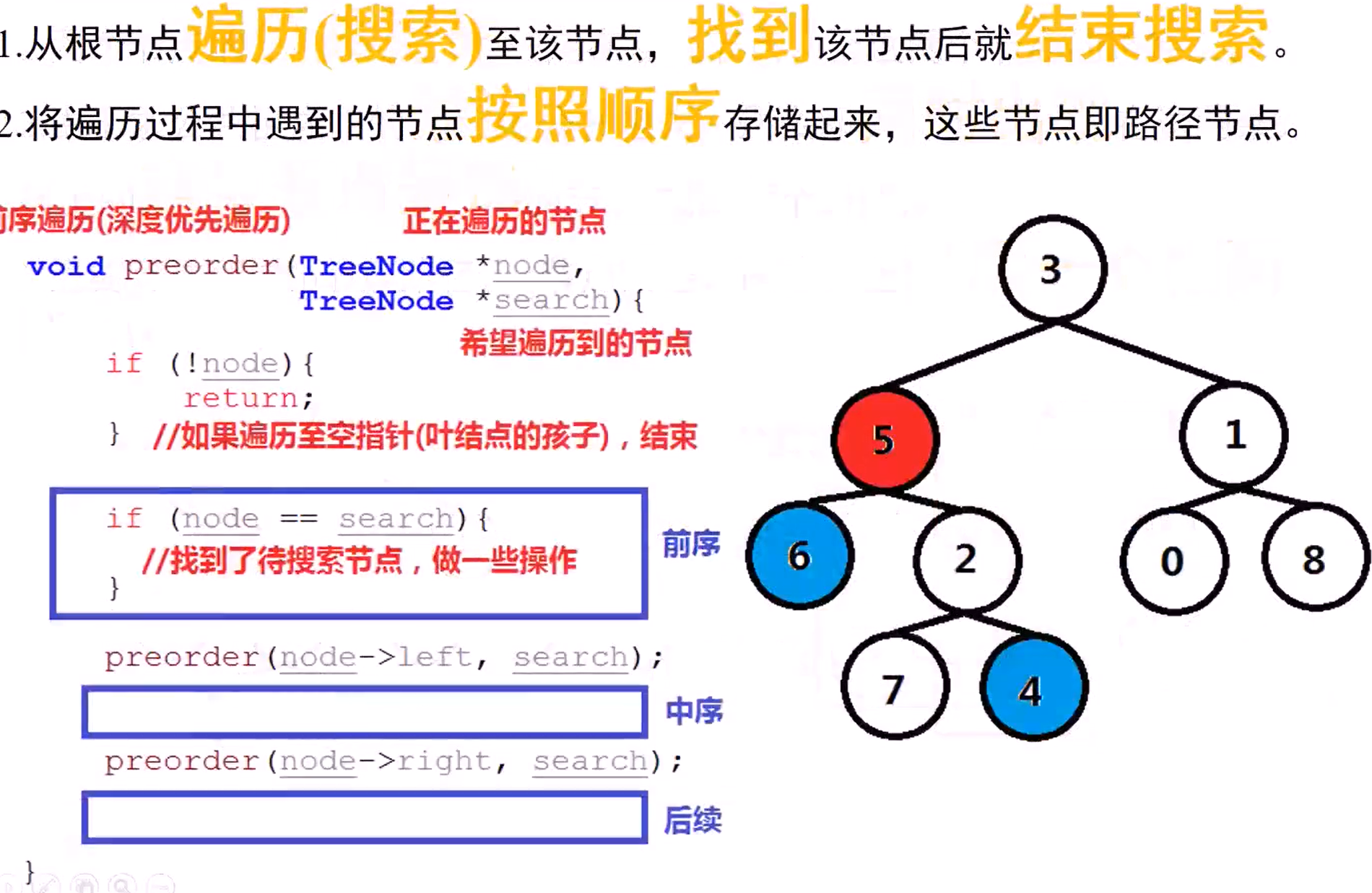
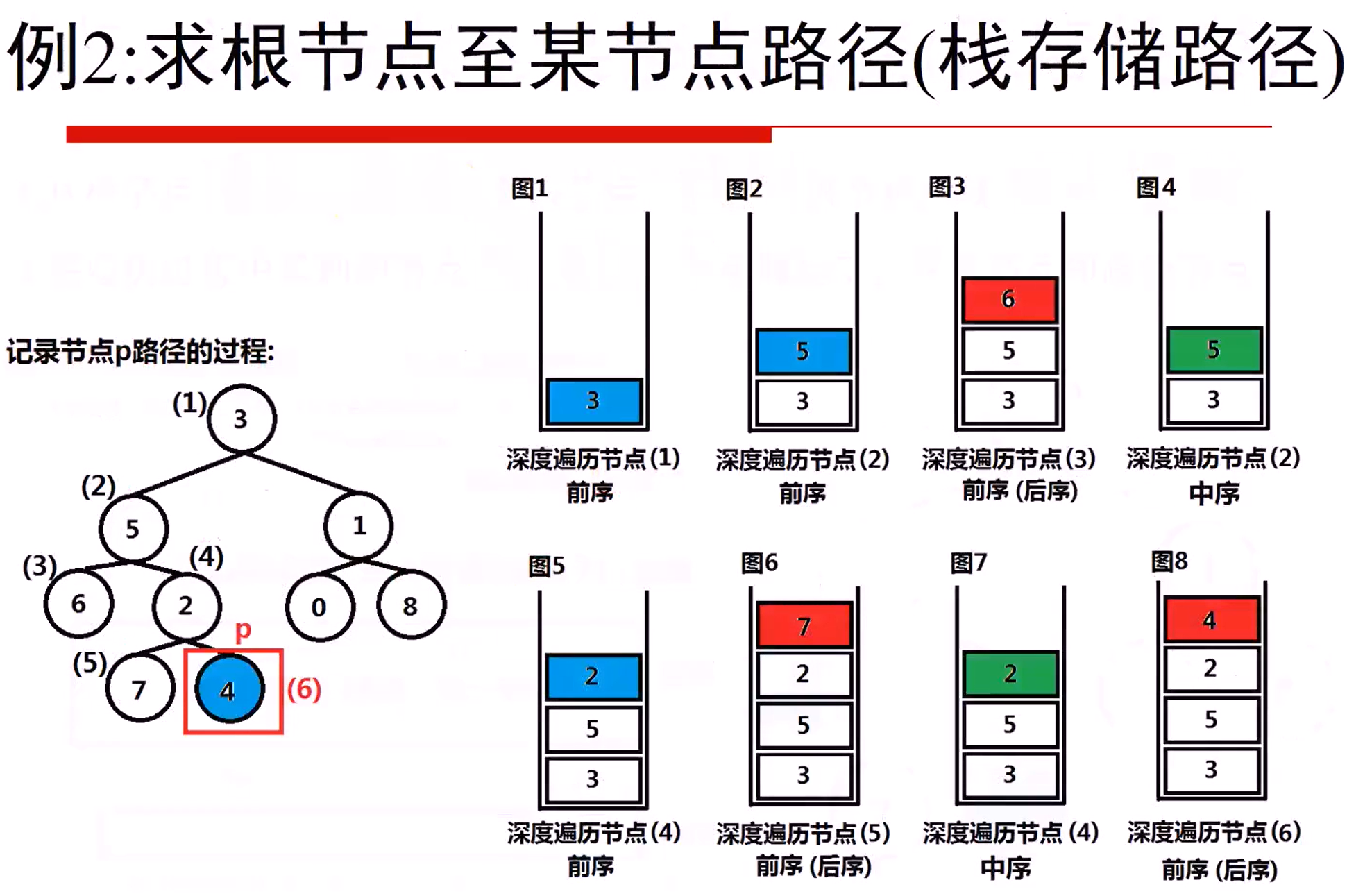
#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>

using namespace std;

struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution
{
private:
    void preorder(TreeNode *node,           //正在遍历的节点
                  TreeNode *search,         //待搜索的节点
                  vector<TreeNode *> &path, //遍历时的节点路径栈
                  vector<TreeNode *> &result,
                  int &finish //记录是否找到search节点，未找到0，找到1
    )
    {
        if (!node || finish == 1)
        {
            return;
        }

        path.push_back(node); //先序遍历时，将节点压入path栈
        if (node == search)
        {
            finish = 1;
            //2 将当前的path存储到result中
            result = path;
        }

        preorder(node->left, search, path, result, finish);
        preorder(node->right, search, path, result, finish);

        //3 结束遍历node时，将node节点弹出path栈
        path.pop_back();
    }

public:
    TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
    {
        vector<TreeNode *> path; //声名遍历用的临时栈
        vector<TreeNode *> node_p_path;
        vector<TreeNode *> node_q_path;

        int finish = 0;

        //1
        preorder(root, p, path, node_p_path, finish);

        path.clear();
        finish = 0; //清空path,finish,计算q节点路径

        preorder(root, q, path, node_q_path, finish);
        int path_len = 0; //较短路径的长度
        if (/*2*/ node_p_path.size() < node_q_path.size())
        {
            path_len = node_p_path.size();
        }
        else
        {
            path_len = node_q_path.size();
        }

        TreeNode *result = 0; // 同时遍历根到pq两个节点的路径上的节点
        for (int i = 0; i < path_len; i++)
        {
            if (/*3*/ node_p_path[i] == node_q_path[i])
            {
                result = node_p_path[i];
            }
        }
        return result;
    }
};

int main()
{
    TreeNode a(3);
    TreeNode b(5);
    TreeNode c(1);
    TreeNode d(6);
    TreeNode e(2);
    TreeNode f(0);
    TreeNode x(8);
    TreeNode y(7);
    TreeNode z(4);

    a.left = &b;
    a.right = &c;
    b.left = &d;
    b.right = &e;
    c.left = &f;
    c.right = &x;
    e.left = &y;
    e.right = &z;
    Solution solve;

    TreeNode *result = solve.lowestCommonAncestor(&a, &b, &f);
    printf("LCA -> %d\n", result->val);

    result = solve.lowestCommonAncestor(&a, &d, &z);
    printf("LCA -> %d\n", result->val);

    result = solve.lowestCommonAncestor(&a, &b, &y);
    printf("LCA -> %d\n", result->val);

    return 0;
}

Java
- 从根节点开始遍历树。
- 在找到 p 和 q 之前，将父指针存储在字典中。
- 一旦我们找到了 p 和 q，我们就可以使用父亲字典获得 p 的所有祖先，并添加到一个称为祖先的集合中。
- 同样，我们遍历节点 q 的祖先。如果祖先存在于为 p 设置的祖先中，这意味着这是 p 和 q 之间的第一个共同祖先（同时向上遍历），因此这是 LCA 节点。

class Solution {

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        // Stack for tree traversal
        Deque<TreeNode> stack = new ArrayDeque<>();

        // HashMap for parent pointers
        Map<TreeNode, TreeNode> parent = new HashMap<>();

        parent.put(root, null);
        stack.push(root);

        // Iterate until we find both the nodes p and q
        while (!parent.containsKey(p) || !parent.containsKey(q)) {

            TreeNode node = stack.pop();

            // While traversing the tree, keep saving the parent pointers.
            if (node.left != null) {
                parent.put(node.left, node);
                stack.push(node.left);
            }
            if (node.right != null) {
                parent.put(node.right, node);
                stack.push(node.right);
            }
        }

        // Ancestors set() for node p.
        Set<TreeNode> ancestors = new HashSet<>();

        // Process all ancestors for node p using parent pointers.
        while (p != null) {
            ancestors.add(p);
            p = parent.get(p);
        }

        // The first ancestor of q which appears in
        // p's ancestor set() is their lowest common ancestor.
        while (!ancestors.contains(q))
            q = parent.get(q);
        return q;
    }

}

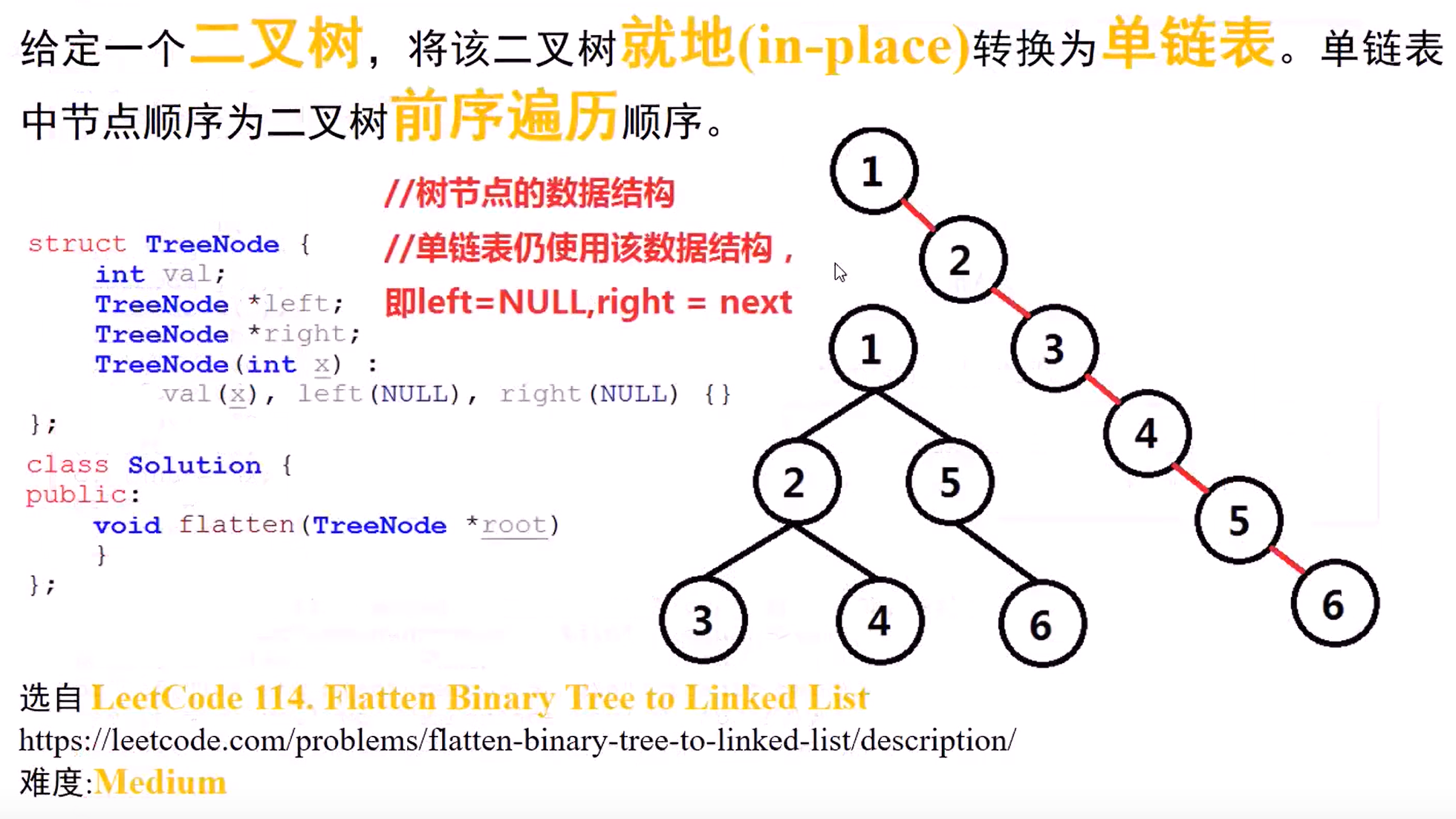
114 Flatten Binary Tree to Linked List(Medium)

Given a binary tree, flatten it to a linked list in-place

给定一个二叉树，原地将它展开为链表

78分钟

二叉树#

二叉树基础#

113 Path Sum II(Medium)#

236 Lowest Common Ancestor of a Binary Tree(Medium)#

114 Flatten Binary Tree to Linked List(Medium)#

二叉树

二叉树基础

113 Path Sum II(Medium)

236 Lowest Common Ancestor of a Binary Tree(Medium)

114 Flatten Binary Tree to Linked List(Medium)