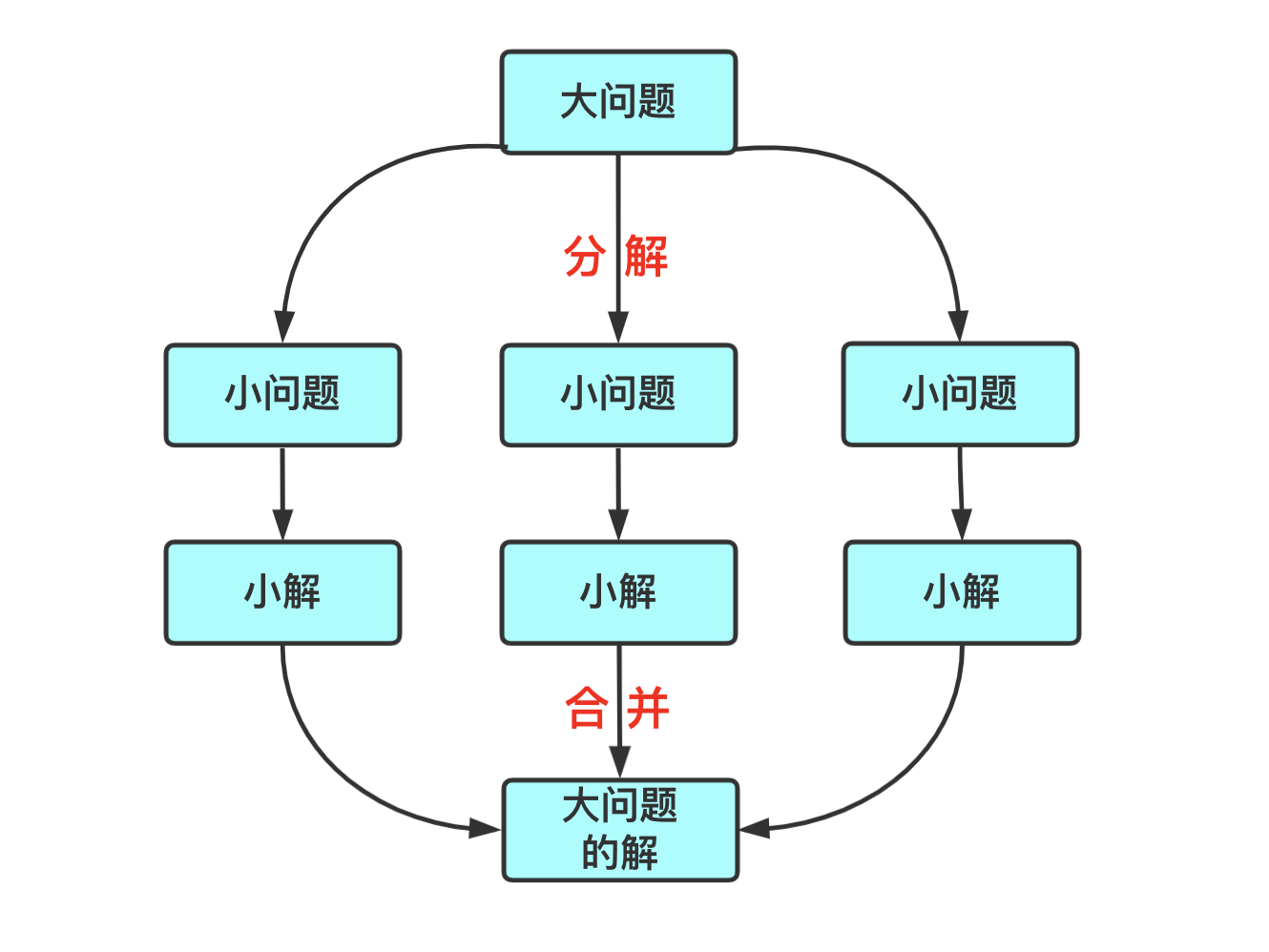
分治法

将大问题分解成若干个小问题，分别求解，再讲小问题的解合并为大问题的解

Leetcode题目

• 169.多数元素
• 53.最大子序和
• 215.数组中k大元素

主定理（Master Theorem）

主定理 是分治法通常遵守的一种通用模式

• 解决规模为 n 的问题，分解成 a 个规模为 n / b 的子问题，然后在 O(n ^ d) 时间内将子问题的解合并起来
• 算法运行时间为：T(n) = aT(n / b) + O(n ^ d); a > 0; b > 1; d ≥ 0
  • 当d > log_b (a)，则T(n) = O(n ^ d)
  • 当d = log_b (a)，则T(n) = O(n ^ d * logn)
  • 当d < log_b (a)，则T(n) = O(n ^ (log_b (a)))
• 例如 归并排序 ，T(n) = 2T(n / 2) + O(n)，a = 2，b = 2，d = 1，即d = log_b (a)，则T(n) = O(n ^ d * logn) = O(nlogn)

归并排序

归并排序是经典的分治法实践算法

• 对于数列7 8 4 1 6 5 2 3，将其按从小到大排序
• 将数列不断二分，对每个子数列进行排序，递归
• 直到分解到单个数字，然后向上合并
• 逐层排序，然后合并，直到顶层，整个数列排序完毕