Version: Next

B-tree

B树是一种平衡的多叉搜索树，多用于文件系统、数据库的实现

  • 1个节点可以存储超过2个元素，可以拥有超过2个子节点
  • 拥有二叉搜索树的一些性质
  • 平衡，每个节点的所有子树高度一致
  • 矮

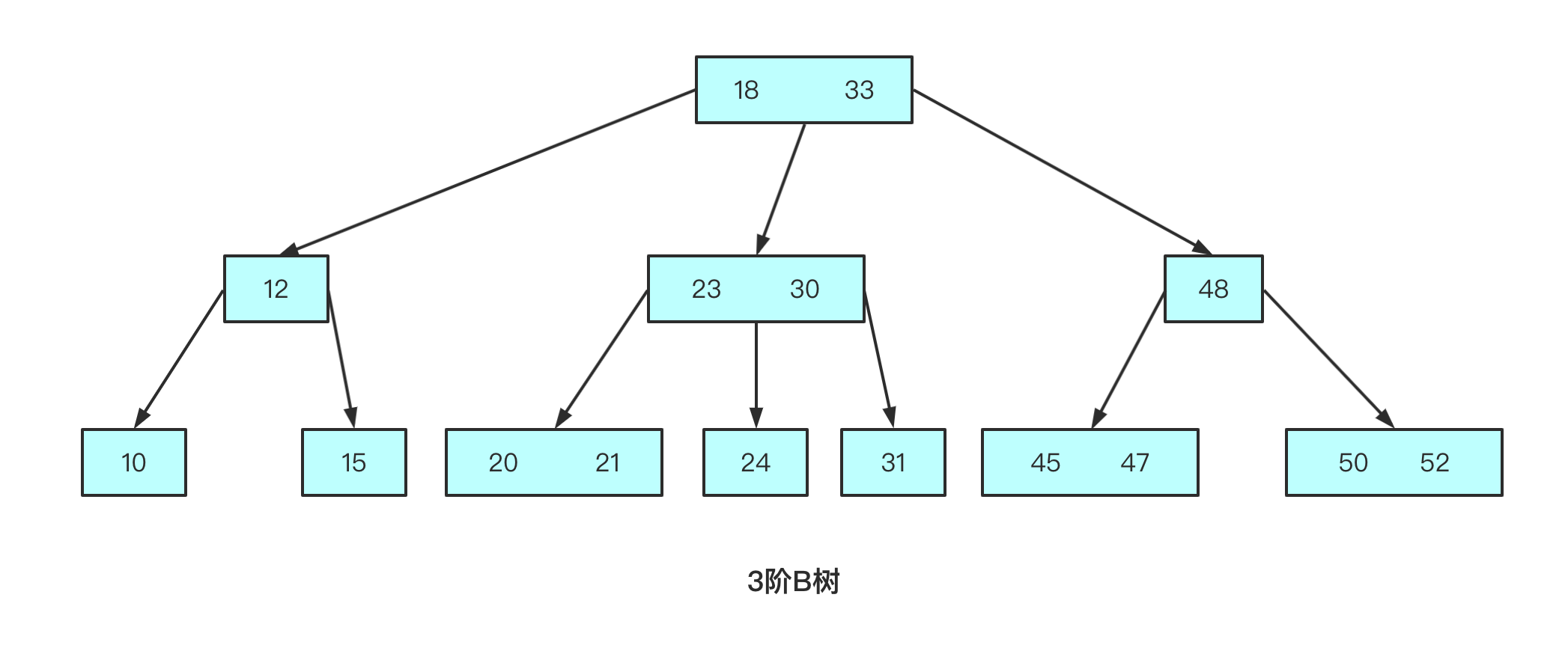
image-20201106143549279

m阶B树的性质（m ≥ 2）

m阶，就是指，1个节点最多可以有m个子节点

性质

  • 假设一个节点存储元素的个数为x
    • 根节点： 1 ≤ x ≤ m-1
    • 非根节点： 向上取整(m/2) - 1 ≤ x ≤ m-1
    • 如果有子节点，则子节点个数 y = x + 1
      • 根节点：2 ≤ y ≤ m
      • 非根节点：向上取整(m/2) ≤ y ≤ m

B树与二叉搜索树

当m = 2时，二阶B树即二叉搜索树

  • B树和二叉搜索树，在逻辑上是等价的
  • 多代节点合并，可以获得一个超级节点（可以存储多个元素的节点）
    • n代合并的超级节点，最多拥有2 ^ n个子节点（至少是2 ^ n阶B树）
  • m阶B树，最多需要logm代合并

搜索

  1. 先在节点内部从小到大开始搜索元素
  2. 如果命中；搜索结束
  3. 如果没有命中，再去对应的子节点中搜索元素，重复步骤1

添加

  • 新添加的元素必定是添加到叶子节点的

上溢

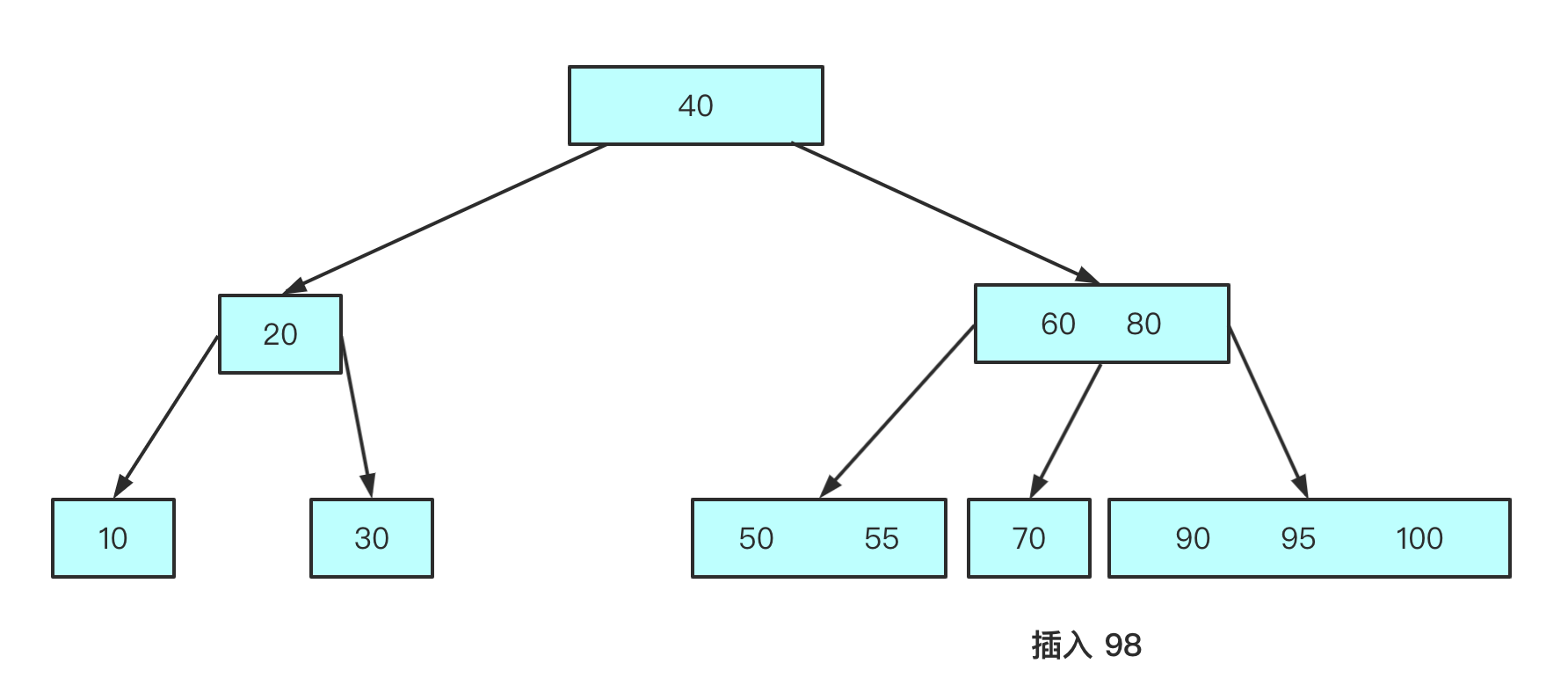
image-20201106154841570

  • 假设是4阶B树
  • 最右下角的叶子节点上限为3，插入98，会导致节点元素个数超出限制
  • 这种现象称为上溢（Overflow）

上溢的解决

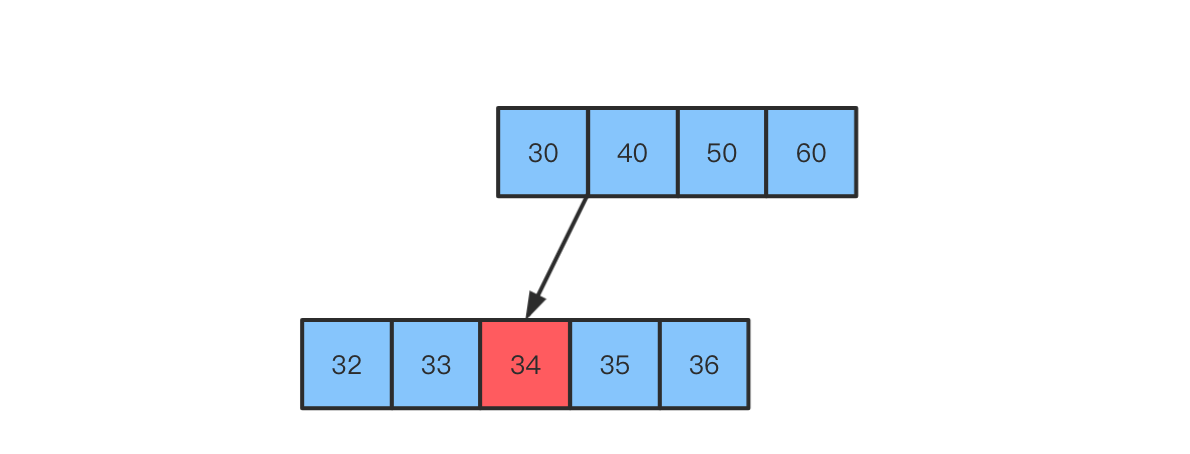
image-20201106155623520

假设5阶B树

  • 上溢节点的元素个数必然等于m（此处为5）
  • 求出上溢节点中最中间元素的位置k，假设最中间元素的位置为k
  • 将k位置对应的元素，向上与父节点进行合并
  • 将 [0, k-1]和[k+1, m-1]位置的元素分裂成2个子节点
    • 分裂之后，2个子节点的元素个数，必然不会低于最低限制向上取整(m/2) - 1

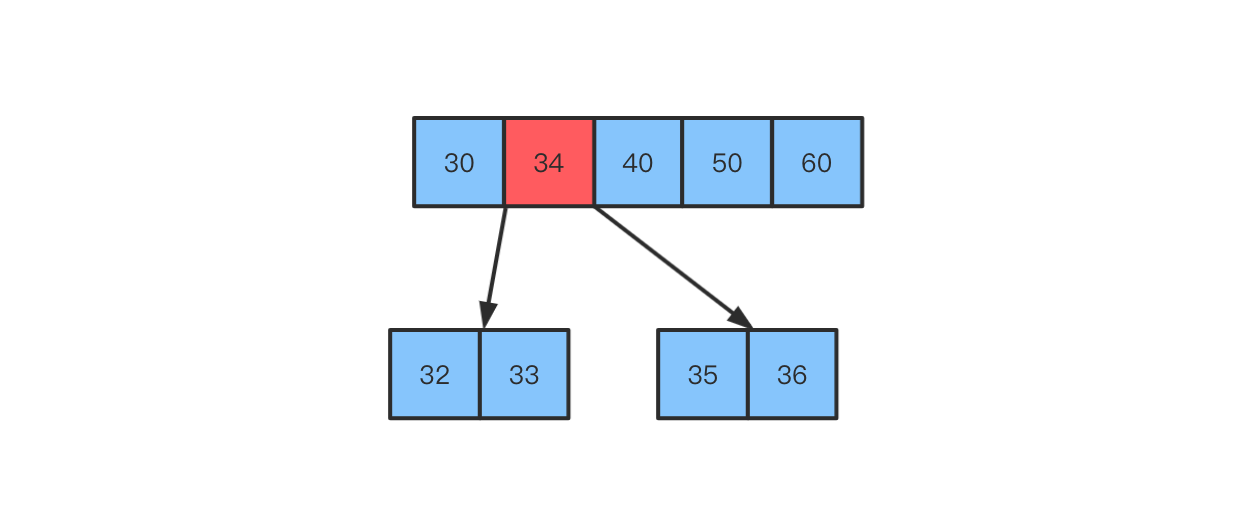
image-20201106160103378

问题

这种做法可能导致父节点再次发生上溢，继续向上合并即可

  • 极端情况下，可能一直分裂到根节点
  • 这是唯一一种会让B树高度变高的情况

删除

删除叶子节点

直接删除即可

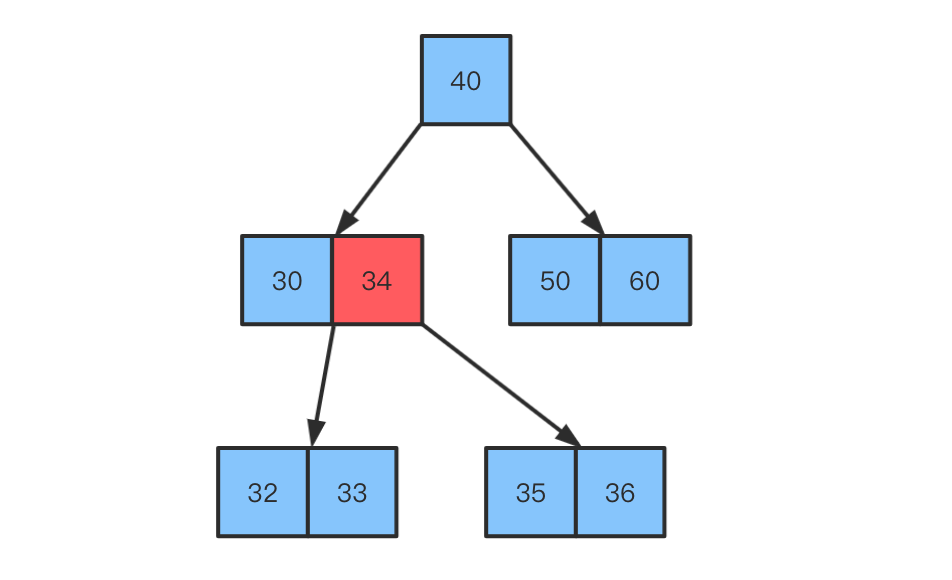
删除非叶子节点

要删除的节点在非叶子节点中

  1. 先找到前驱或者后继元素，覆盖所需删除元素的值
  2. 删除前驱或者后继元素
注意

在B树中

  1. 非叶子节点的前驱或者后继元素，必定在叶子节点中
  2. 推出，被删除的本质上还是叶子节点
结论

在B树中，真正的被删除元素，一定是叶子节点

下溢

叶子节点被删除掉一个元素后，元素个数可能小于m阶B树的最低限制向上取整(m /2) - 1

这种现象称为下溢（underflow）

下溢的解决

  • 下溢节点的元素数量必然等于向上取整(m / 2) - 2
  • 如果下溢节点临近的兄弟节点，有至少向上取整(m/2)个元素，可以向其借1个元素
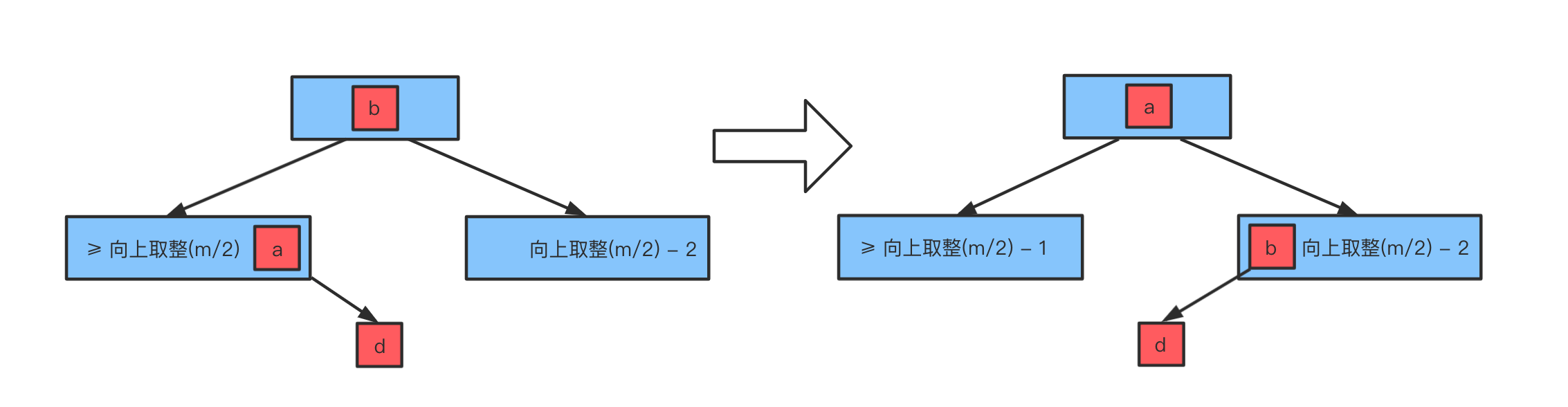
    • 将父节点的元素b插入到下溢节点的0位置（最小位置、最左侧位置）
    • 用兄弟节点的元素a（最大元素）替代父节点的元素b
    • 这种操作，实际上就是旋转（图中b节点进行右旋）

image-20201109164053639

问题：如果兄弟节点正好只有向上取整(m/2) - 1个元素，不能再借出一个元素，该怎么办呢

  • 将父节点的元素b挪下来跟左右节点进行合并
  • 合并后的节点元素个数等于向上取整(m/2) + 向上取整(m/2) - 2，不超过m - 1

image-20201109162214813

注意

这个操作可能导致父节点下溢，依然按照上述方法解决，下溢现象可能一直向上传播

总结

下溢的解决

  1. 先看能不能从兄弟节点借一个元素过来，实现旋转
  2. 如果兄弟节点借不来元素，则将父节点中央元素挪下来和左右子节点一起合并

4阶B树

先学习4阶B树，将能更好的学习理解红黑树

4阶B树的性质：

  • 所有节点能存储的元素个数x ∈ [1, 3]
  • 所有非叶子节点的子节点个数y ∈ [2, 4]
练习

手动模拟4阶B树添加与删除元素的过程

  • 从1添加到22
  • 从1删除到22

观察、分析4阶B树的运作方式

使用算法可视化网站验证结果