Version: Next
希尔排序
Shell Sort
- 1959 年由 Donald Shell 提出
- 希尔排序将序列看成一个
矩阵,分为m列,进列逐行排列
m会从某个整数逐渐减为1- 当
m = 1,整个序列缩成一列,就完成了排序- 也被称为
递减增量排序(Diminishing Increment Sort)- 矩阵的列数取决于
步长序列step sequence
- 如果步长序列为 {1, 5, 19, 41, 109}
- 表示依次分为 109、41、19、5、1 列
- 不同的步长序列,执行效率不同
- 希尔本人给出的步长序列为
n / 2^k,其中 n 为元素数目,k 为从1开始的正整数- 比如 n = 16,步长序列为 {1, 2, 4, 8}
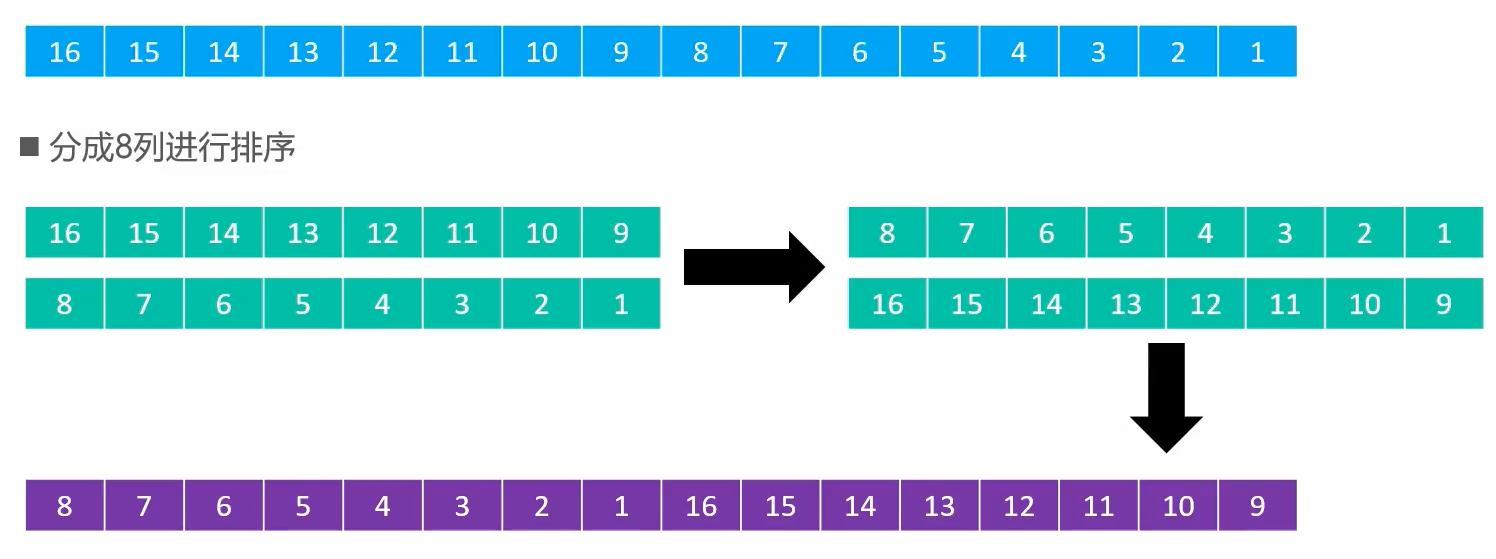
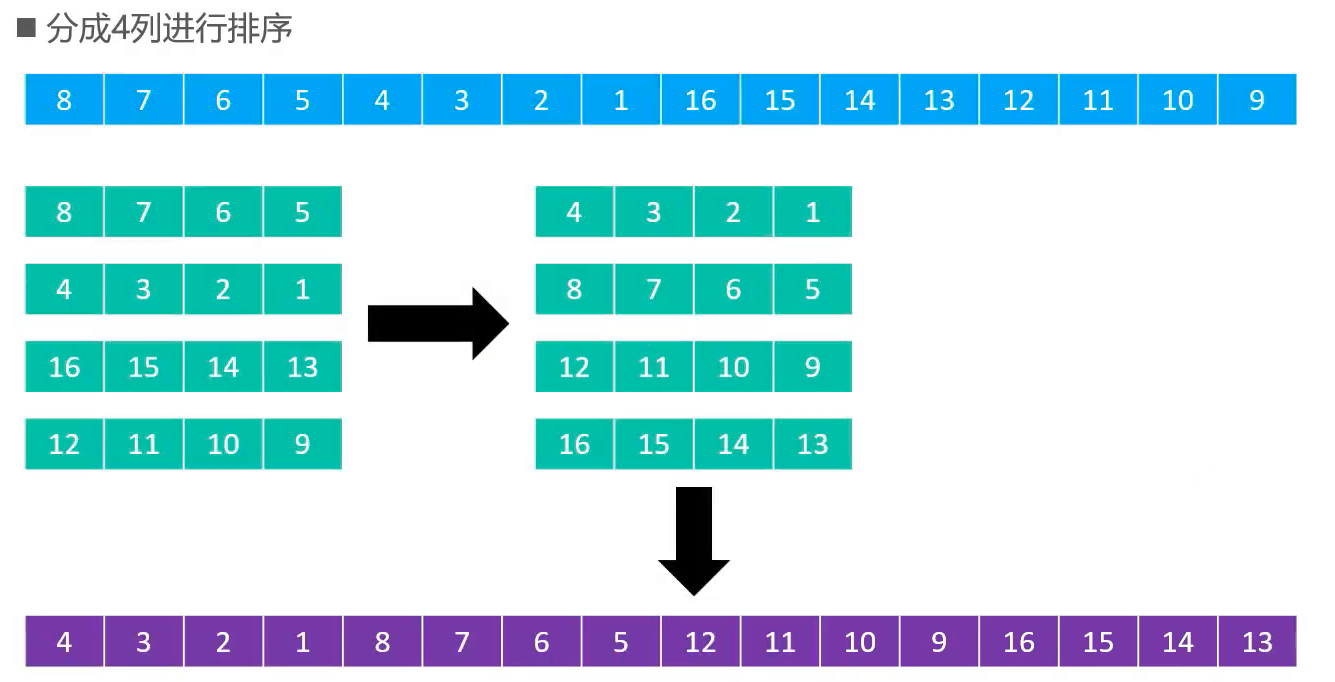
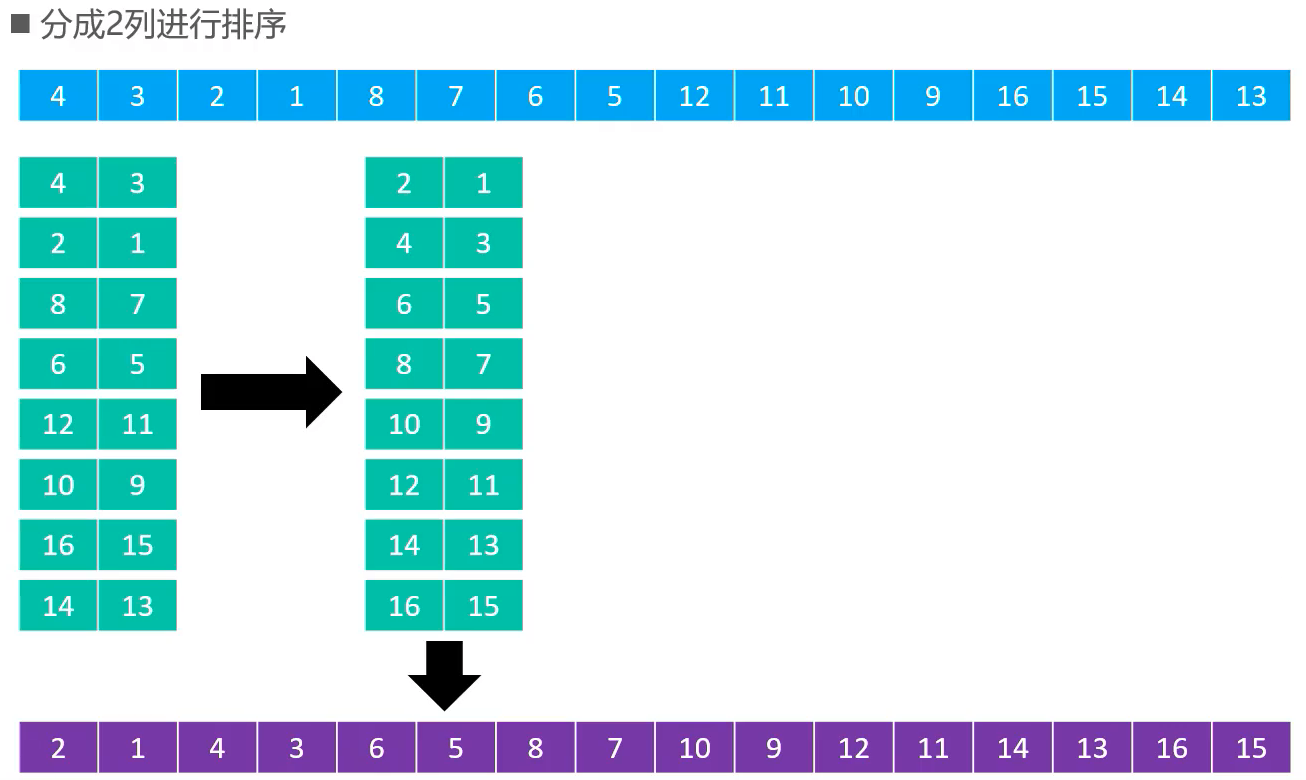
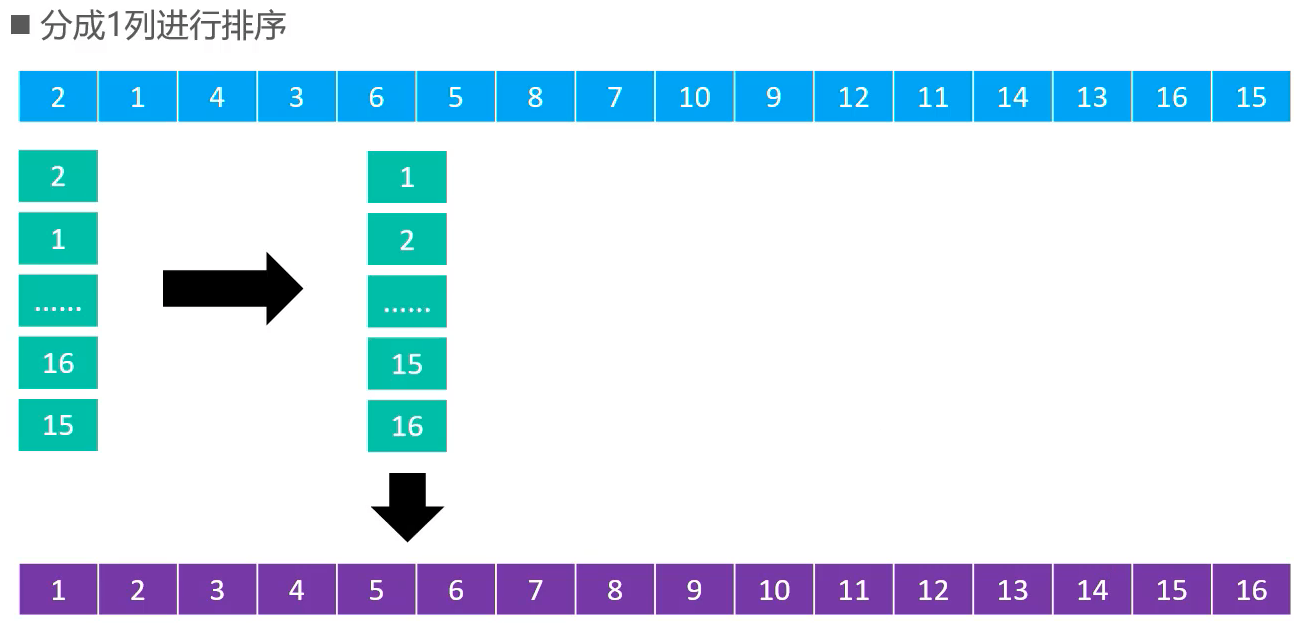
问题
为什么不直接弄成一列排序
- 每一次排序,序列中的
逆序对数目都会减少 - 因此,希尔排序底层一般使用插入排序对每一列进行排序
- 很多资料认为希尔排序是对插入排序的改进
实现
- 生成步长序列
- 遍历步长,逐列进行排序
- 要实现逐列,就是在原数组上,按
step步长跳着走,只选中部分元素进行插入排序- 假设元素在第
col列,第row行,步长(总列数)是step
- 那么元素在数组中的索引时
col + row * step(从0开始数)
col:对 step 的遍历值- 初始位置为
col + step然后与current - step即前一个元素进行比较current边界条件是大于当前 列col
/**
* 希尔排序
*/
public class ShellSort<E extends Comparable<E>> extends Sort<E> {
public ShellSort(E[] array) {
this.array = array;
}
@Override
public void sort() {
List<Integer> stepSequence;
// 调用方法得到步长序列 例 {8,4,2,1} 按照希尔给出的写
stepSequence = shellStepSequence();
for (Integer step : stepSequence) {
shellSort(step); // 希尔排序
}
}
/**
* 分成 step 列进行排序
*
* @param step 步长序列中的一个成员,代表当前分成多少 "列" 进行排序
*/
private void shellSort(int step) {
for (int col = 0; col < step; col++) { // 逐列
insertSort(col, step); // 插入排序
}
}
private List<Integer> shellStepSequence() {
List<Integer> stepSequence = new ArrayList<>();
int division = this.array.length;
while ((division >>= 1) > 0)
stepSequence.add(division);
return stepSequence;
}
// 插入排序
private void insertSort(int col, int step) {
// col col+step col + 2step col + 3step ...
for (int begin = col + step; begin < array.length; begin += step) {
int current = begin;
while (current > col && cmp(current, current - step) < 0) {
swap(current, current - step);
current -= step;
}
}
}
public static void main(String[] args) {
Integer[] array = {4, 2, 3, 1};
ShellSort<Integer> integerShellSort = new ShellSort<>(array);
integerShellSort.sort();
for (Integer integer : array) {
System.out.println(integer + " ");
}
}
}
关于步长序列
- 希尔本人给出的步长序列,最坏时间复杂度是
O(n ^ 2) - 目前已知最好的补偿序列,最坏时间复杂度是
O(n ^ (4/3)),1986 年由 Robert Sedgewick 提出
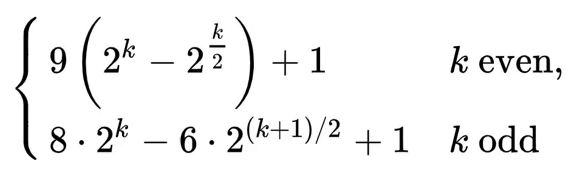
值为 1、5、19、41、109 ...