72.编辑距离

72. 编辑距离

难度 困难

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

Given two strings word1 and word2, return the minimum number of operations required to convert word1 to word2.

You have the following three operations permitted on a word:

Insert a character Delete a character Replace a character

示例 1：

输入：word1 = "horse", word2 = "ros"

输出：3

解释：

horse -> rorse (将 'h' 替换为 'r')

rorse -> rose (删除 'r')

rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"

输出：5

解释：

intention -> inention (删除 't')

inention -> enention (将 'i' 替换为 'e')

enention -> exention (将 'n' 替换为 'x')

exention -> exection (将 'n' 替换为 'c')

exection -> execution (插入 'u')

提示：

• 0 <= word1.length, word2.length <= 500
• word1 和 word2 由小写英文字母组成

动态规划

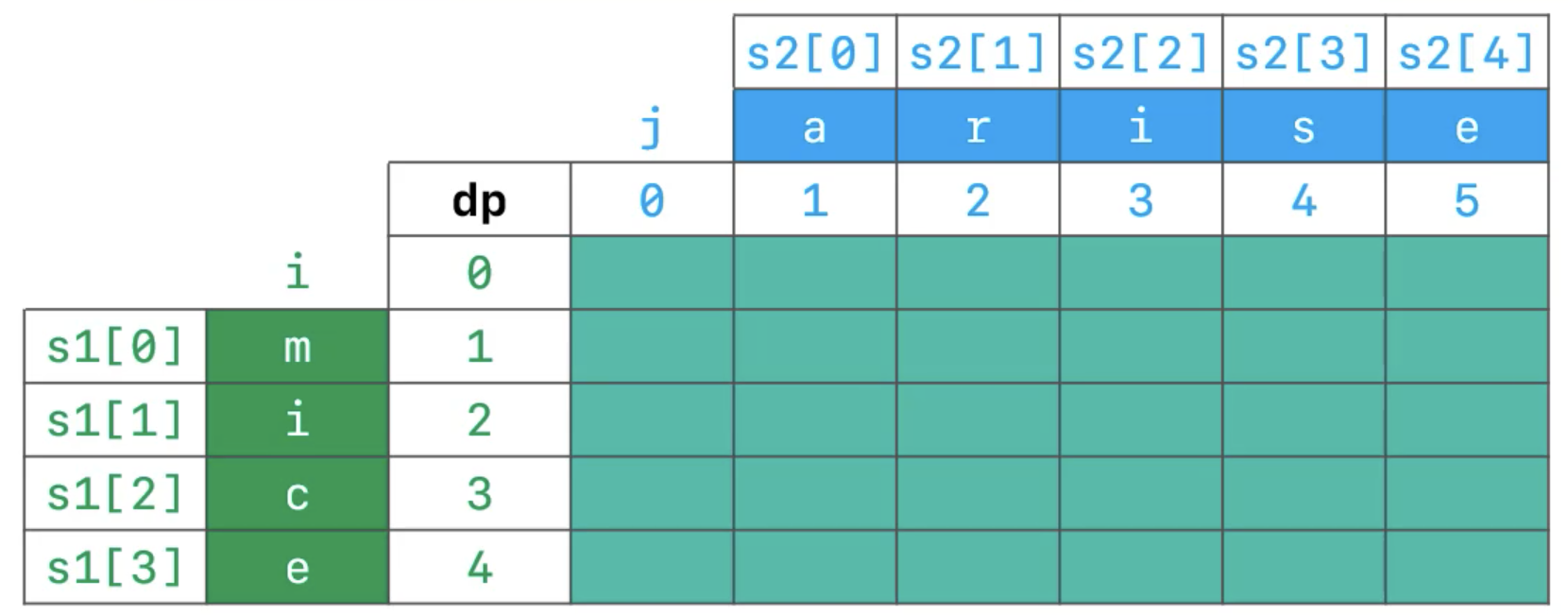
假设从单词 mice 变到单词 arise

• 令 s1 = mice，长度为 n1
• 令 s2 = arise，长度为 n2
• dp 是大小为 [n1 + 1][n2 + 1] 的二维数组
• dp[i][j] 表示从 子串s1[0, j) 转化到 子串s2[0, j) 的最少操作数
  • s1[0, i) 是由 s1 的前 i 个字符组成的子串
  • s2[0, j) 是由 s2 的前 j 个字符组成的子串
• 则 dp[n1][n2] 就是最终答案，表示 s1[0, n1) 到 s2[0, n2) 的最少操作数

状态转移方程

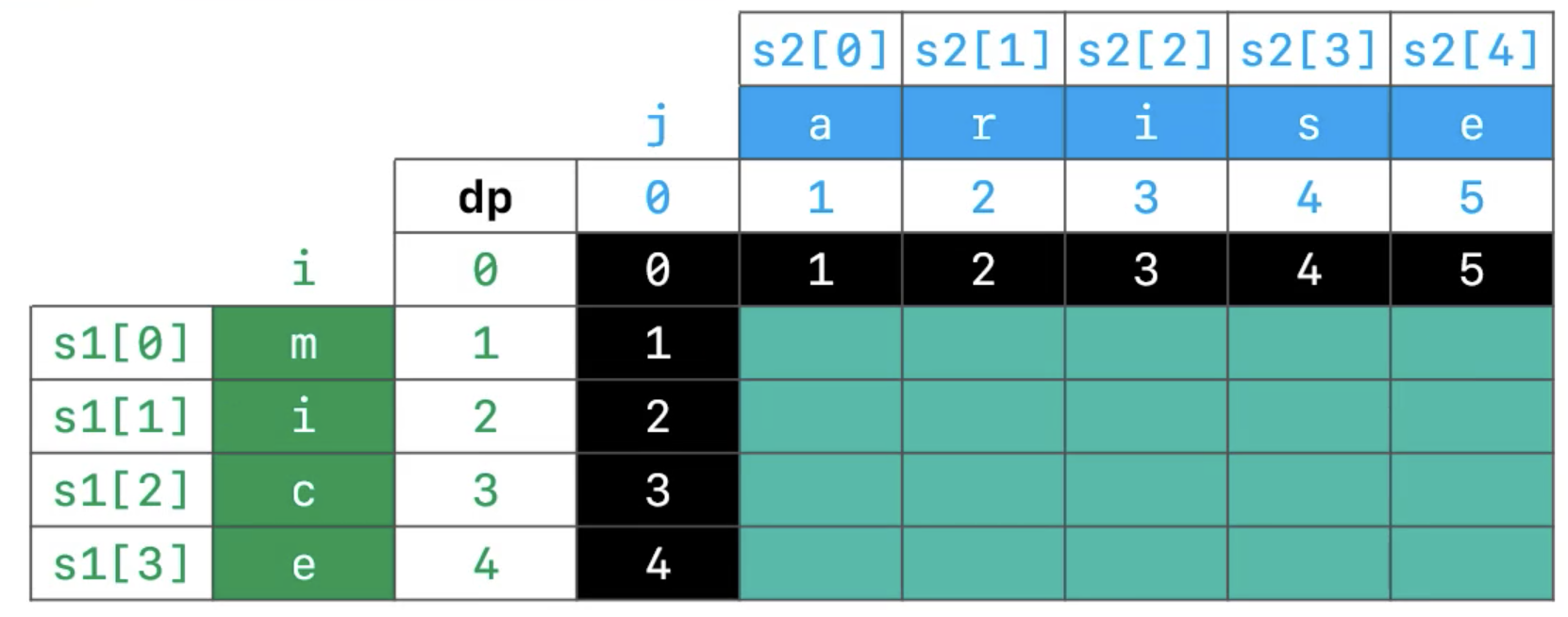
• 最左上角 dp[0][0] 表示 s1 空子串转换到 s2 空子串的最少操作数，显然等于 0
• 第0行、第0列表示从 空串 转到 非空串 需要的最少操作，显然等于 非空串 的长度
  • 对于第0列：dp[i][0] = i
  • 对于第0行：dp[0][j] = j

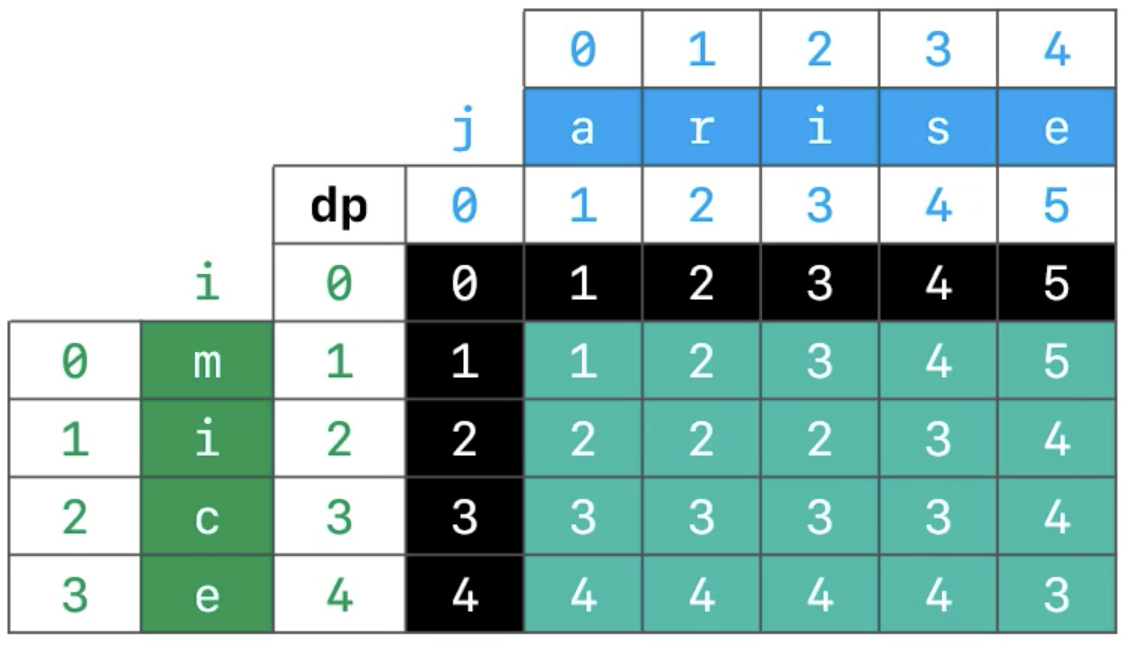
从 第1列、第1行开始为一般情况

• 求出一般的 dp[i][j]
• 分为 4 种情况讨论：
  1. 先 删除 s1[0, i) 的最后一个字符得到 s1[0, i - 1)
     • 再从 s1[0, i - 1) 转化为 s2[0, j)
     • 这种情况下，dp[i][j] = 1 + dp[i - 1][j]
  2. 先由 s1[0, i) 转换为 s2[0, j - 1)，然后在最后 插入 字符 s2[j - 1]，得到 s2[0, j)，此时 dp[i][j] = dp[i][j - 1] + 1
  3. 如果子串的最后一个字符不同： s1[i - 1] != s2[j - 1]，先由 s1[0, i - 1) 转换到 s2[0, j - 1)，就是看出了最后一个字符以外的部分，如何相互转换。在此基础上，再调整最后一个原本不相同的字符即可
     • dp[i][j] = dp[i - 1][j - 1] + 1
  4. 如果子串的最后一个字符相等： s1[i - 1] == s2[j - 1]，那么从 s1[0, i - 1) 转换到 s2[0, j - 1) 后，不需要进行任何额外操作
     • dp[i][j] = dp[i - 1][j - 1]
• 上述 4 种情况，其中 情况3 和 情况4 为二选一
  • 最终的 dp[i][j] 为
    • 情况1：dp[i][j] = 1 + dp[i - 1][j]
    • 情况2：dp[i][j] = dp[i][j - 1] + 1
    • 情况3/4：dp[i][j] = dp[i - 1][j - 1] + 1 或 dp[i][j] = dp[i - 1][j - 1]
  • 三者中的 最小值

public int minDistance(String word1, String word2) {

if (word1.length() == 0 && word2.length() == 0) return 0;

if (word1.length() == 0) return word2.length();

if (word2.length() == 0) return word1.length();

char[] chars1 = word1.toCharArray();

char[] chars2 = word2.toCharArray();

int[][] dp = new int[chars1.length + 1][chars2.length + 1];

dp[0][0] = 0;

for (int i = 1; i <= chars1.length; i++) // 第0列，遍历所有行

dp[i][0] = i;

for (int j = 1; j <= chars2.length; j++) // 第0行，遍历所有列

dp[0][j] = j;

// 从第一行第一列开始为一般情况，分为4种情况讨论

for (int i = 1; i <= chars1.length; i++) {

for (int j = 1; j <= chars2.length; j++) {

// 1. 先 `删除` `s1[0, i)` 的最后一个字符得到 `s1[0, i - 1)`

// 上面那个格子

int top = dp[i - 1][j] + 1;

// 2. 先由 `s1[0, i)` 转换为 `s2[0, j - 1)`，然后在最后 `插入` 字符 `s2[j - 1]`，得到 `s2[0, j)`，

// 左边那个格子

int left = dp[i][j - 1] + 1;

// 左上角 行列都 - 1

int leftTop = dp[i - 1][j - 1];

// 3. 如果子串的最后一个字符不同

if (chars1[i - 1] != chars2[j - 1]) leftTop++;

// 三者取最小

dp[i][j] = Math.min(Math.min(left, top), leftTop);

}

}

// 返回最右下角的格子

return dp[chars1.length][chars2.length];

}