Version: Next

1143.最长公共子序列

难度 中等

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。

若这两个字符串没有公共子序列，则返回 0。

示例 1:

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace"，它的长度为 3。

示例 2:

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。

示例 3:

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0。

提示:

1 <= text1.length <= 1000
1 <= text2.length <= 1000
输入的字符串只含有小写英文字符。

Given two strings text1 and text2, return the length of their longest common subsequence.

A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, "ace" is a subsequence of "abcde" while "aec" is not). A common subsequence of two strings is a subsequence that is common to both strings.

If there is no common subsequence, return 0.

Example 1:

Input: text1 = "abcde", text2 = "ace" Output: 3
Explanation: The longest common subsequence is "ace" and its length is 3. Example 2:

Input: text1 = "abc", text2 = "abc" Output: 3 Explanation: The longest common subsequence is "abc" and its length is 3. Example 3:

Input: text1 = "abc", text2 = "def" Output: 0 Explanation: There is no such common subsequence, so the result is 0.

动态规划

定义状态
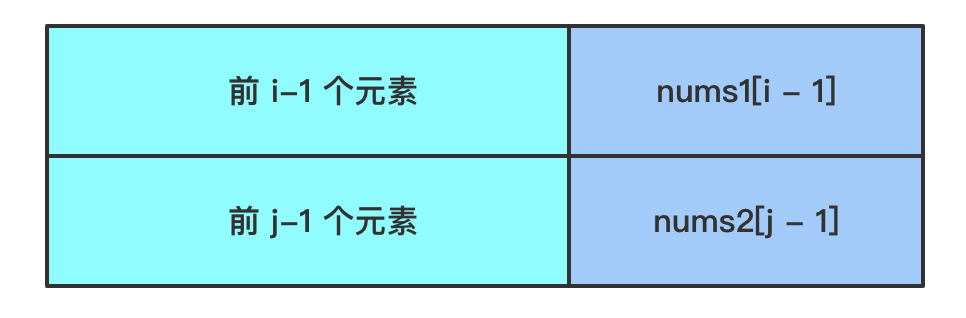
假设 dp(i, j) 是 nums1 前 i 个元素与 nums2 前 j 个元素的最长公共子序列长度
所求解即为 dp(nums1.length, nums2.length)
初始条件
两个序列，其中一个为空，则：dp(i, 0) = dp(0, j) = 0
状态转移方程：如何实现 dp(i - 1, j - 1) -> dp(i, j)
所求 dp(i, j) 即上图两个序列的最长公共子序列
如果两个序列的最后一个元素相等，即 nums1[i - 1] = nums2[j - 1]，则 dp(i, j) = dp(i - 1, j - 1) + 1
如果两个序列的最后一个元素不相等，即 nums1[i - 1] ≠ nums2[j - 1]，那么看看这边的新元素在对面前面的元素中有没有一样的，反之亦然，然后求二者的最大值，则 dp(i, j) = max{ dp(i - 1, j), dp(i, j - 1) }

public class _1143最长公共子序列 {
    public static int longestCommonSubsequence(String text1, String text2) {
        return 0;
    }

    public static int longestCommonSubsequence(int[] nums1, int[] nums2) {
        if (nums1 == null || nums1.length == 0) return 0;
        if (nums2 == null || nums2.length == 0) return 0;

        int[][] dp = new int[nums1.length + 1][nums2.length + 1];

        for (int i = 1; i <= nums1.length; i++) {
            for (int j = 1; j <= nums2.length; j++) {
                if (nums1[i - 1] == nums2[j - 1])
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }

        return dp[nums1.length][nums2.length];
    }

    public static void main(String[] args) {
        int[] nums1 = {1, 3, 5, 9, 10};
        int[] nums2 = {1, 4, 9, 10};

        int res = longestCommonSubsequence(nums1, nums2);
        System.out.println("res = " + res);
    }
}

1143.最长公共子序列#

动态规划#

1143.最长公共子序列

动态规划