堆

一种二叉树的结构——满足一定条件的完全二叉树

堆

• 是一棵完全二叉树
• 每个节点都 ≥或≤ 孩子节点，但是不能说某一层就比另一层大或者小，这是不一定的
  • ≥：称为最大堆、大根堆、大顶堆
  • ≤：称为最小堆、小根堆、小顶堆

堆 也是一种树状的数据结构，但不要跟 JVM 中的堆空间混淆，常见的堆实现主要有

• 二叉堆：Binary Heap 完全二叉堆
• 多叉堆：D-heap、D-ary Heap
• 索引堆：Index Heap
• 二项堆：Binomial Heap
• 斐波那契堆：Fibonacci Heap
• 左倾堆：Leftist Heap
• 斜堆：Skew Heap

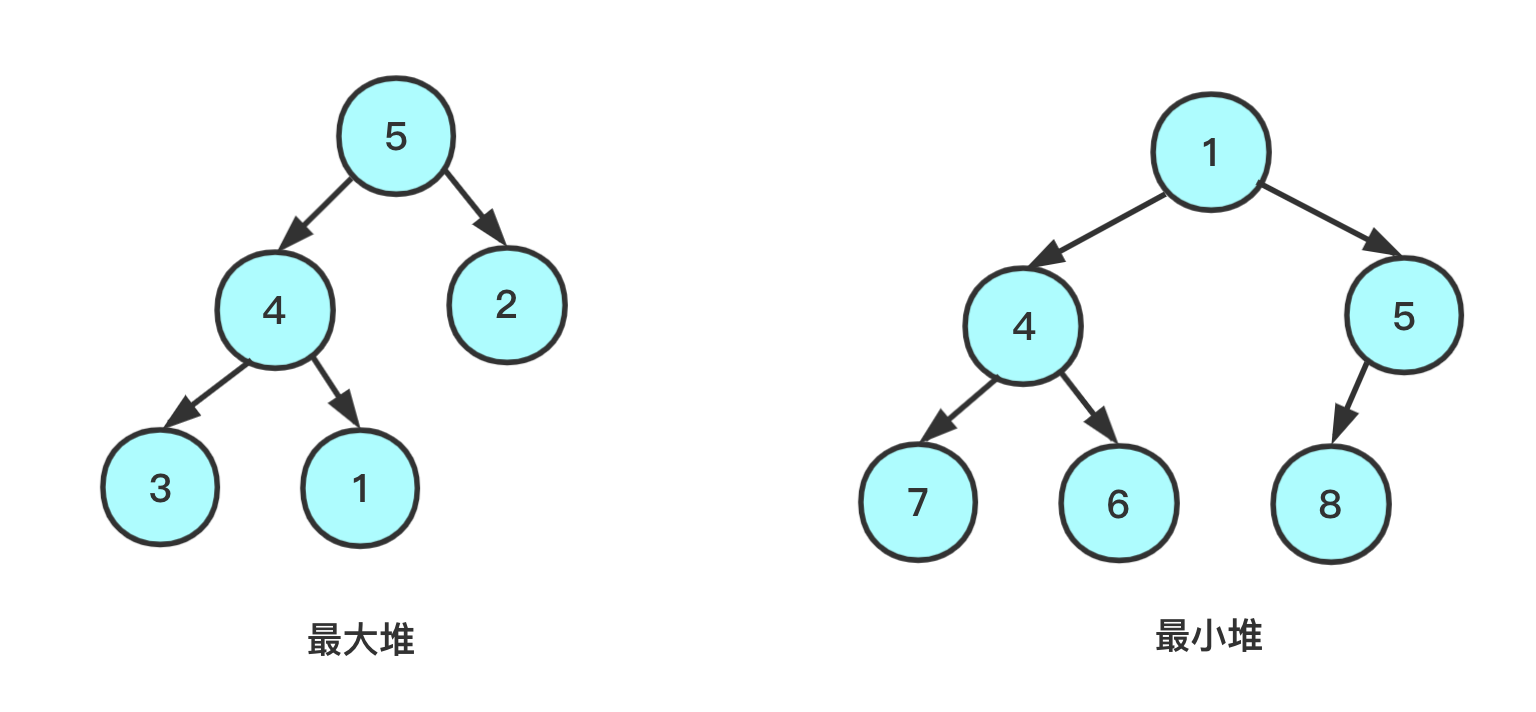
堆顶

• 最大堆：堆顶是最大值
• 最小堆：堆顶是最小值

操作	描述	复杂度
搜索 Search	查看堆顶元素 查看非堆顶	O(1) O(n)
添加 Insert	向堆中添加元素	O(logn)
删除 Delete	删除堆顶元素	O(logn)

堆的常用操作

• 创建堆（最大堆、最小堆）
• 添加元素
• 获取堆顶元素
• 删除堆顶元素
• 堆的长度
• 堆的遍历

leetcode题目

• 215.数组中第k个最大元素
• 692.前k个高频单次

堆接口设计

public interface MyHeap<E> {

int size(); // 元素的数量

boolean isEmpty(); // 是否为空

void clear(); // 清空

void add(E element); // 添加一个元素

E get(); // 获取堆顶元素

E remove(); // 删除堆顶元素

E replace(E element); // 黑手那出堆顶元素的同时插入一个新元素

}

二叉堆

• 二叉堆 的逻辑结构就是一颗完全二叉树，所以也叫 完全二叉堆
• 鉴于完全二叉树的一些特性，二叉堆 的底层一般用 数组 实现即可
  • 因为完全二叉树是从上到下，从左到右依次放置节点的，那么可以按照这个顺序来使用数组下标，类似层序遍历

索引 i 的规律（完全二叉树性质）

• i == 0 ： 根节点
• i > 0：它的 父节点 编号为 floor((i - 1) / 2)
• 左子节点规律（n 为元素总数）
  • 2i + 1 ≤ n - 1：则它的 左子节点 编号为 2i + 1
  • 2i + 1 > n - 1： 则它没有左子节点
• 右子节点规律
  • 2i + 2 ≤ n - 1：则它的 右子节点 编号为 2i + 2
  • 2i + 2 > n - 1： 则它没有右子节点

二叉堆实现

• 定义一个数组，容易想到二叉堆也有 扩容 操作
• 定义 size 记录有效元素数目
• comparator 实现元素比较
• DEFAULT_CAPACITY 默认容量
• 构造方法，要求从外部传入一个 comparator
• int compare(E e1, E e2) 方法，实现元素之间的比较，如果存在外部传入的 comparator 就用这个 comparator 进行比较；否则，强制转换为 Comparable 类型，调用 compareTo 方法
• get() 方法就是返回 根元素，也就是数组的0号元素，注意判空
• 默认容量

public class MyBinaryHeap<E> implements MyHeap<E> {

private E[] elements;

private int size;

private Comparator<E> comparator;

private static final int DEFAULT_CAPACITY = 10;

public MyBinaryHeap(Comparator<E> comparator) {

this.comparator = comparator;

this.elements = (E[]) new Object[DEFAULT_CAPACITY];

}

// 不穿比较器的构造方法，调用一下上面那个构造方法就行了

public MyBinaryHeap() {

this(null);

}

@Override

public int size() {

return this.size;

}

@Override

public boolean isEmpty() {

return this.size == 0;

}

@Override

public void clear() {

for (int i = 0; i < size; i++) {

elements[i] = null;

}

size = 0;

}

@Override

public void add(E element) {

// 待实现

}

@Override

public E get() {

return size == 0 ? null : elements[0];

}

@Override

public E remove() {

// 待实现

return null;

}

@Override

public E replace(E element) {

// 待实现

return null;

}

private int compare(E e1, E e2) {

return comparator != null ? comparator.compare(e1, e2) : ((Comparable<E>) e1).compareTo(e2);

}

}

add 方法

• 向数组的最后一个位置插入新元素，但可能要 扩容

MyArrayList 的扩容代码

/**

* 保证要有capacity的容量

*

* @param capacity 指定容量

*/

private void ensureCapacity(int capacity) {

int oldCapacity = elements.length;

if (oldCapacity > capacity) return;

// 右移一位相当于/2 ， 再加上原值，等于原值的1.5倍

int newCapacity = oldCapacity + (oldCapacity >> 1);

// 建立新数组

E[] newElements = (E[]) new Object[newCapacity];

for (int i = 0; i < size; i++) {

newElements[i] = elements[i];

}

// 引用指向新数组

System.out.format("扩容了，旧容量: %s | 新容量：%s \n", oldCapacity, newCapacity);

elements = newElements;

}

• 放置位置与新元素的值大小有关，比如向大顶堆中添加一个无穷大的元素，那么它应该在 根
• 确定是 大顶堆 还是 小顶堆，这里假设是大顶端
  • 加入新元素，不断的跟 父节点 （floor(i - 1) / 2 就能拿到父节点的下标）进行比较，对于最大堆，任意一个节点必须≥自己的子节点，否则就 交换
    • 循环执行上面这个操作，因为是不断地 除以2 所以复杂度是 O(logn)
    • 如果父节点 ≥ 新节点 || 没有父节点，则退出循环
    • 这一操作学名为 上滤 Sift Up
  • 交换：实现上就是交换数组上的两个元素

siftUp 上滤方法

给定一个索引 index，让个这个索引位置的元素进行上滤

• 获取父节点：首先确保父节点存在，计算公式 floor(i - 1) / 2，那么这个结果必须 ≥ 0，推一下就可以得到，i > 0 就能保证有父节点

上滤

/**

* 对目标索引位置的元素进行上滤操作

* @param index 目标索引

*/

private void siftUp(int index) {

E element = elements[index];

while (index > 0) {

int parentIndex = (index - 1) >> 1; // floor(i - 1) / 2

E parentElement = elements[parentIndex];

// 如果 父节点 >= 新元素 退出循环

if (compare(parentElement, element) >= 0) break;

// 交换

elements[index] = parentElement;

index = parentIndex;

}

elements[index] = element;

}

add 方法实现

1. 检查元素是否存在
2. 检查是否扩容
3. 在数组后面追加新元素
4. 对新元素进行上滤

@Override

public void add(E element) {

elementNotNullCheck(element); // 检查元素可比性

ensureCapacity(size + 1); // 扩容检查

elements[size++] = element; // 插入数组

siftUp(size - 1); // 上滤

}

测试

• 实现 BinaryTreeInfo 接口（自己写的打印树的工具接口)

实现打印接口的4个方法

@Override

public Object root() {

return 0; // 返回索引

}

@Override

public Object left(Object node) {

Integer index = (Integer) node;

index = (index << 1) + 1;

return index >= size ? null : index; // 2i + 1;

}

@Override

public Object right(Object node) {

Integer index = (Integer) node;

index = (index << 1) + 2;

return index >= size ? null : index; // 2i + 2;

}

@Override

public Object string(Object node) {

// 传进来的是索引

Integer index = (Integer) node;

return elements[index];

}

• 向堆中添加一些元素，然后进行打印

public static void main(String[] args) {

MyBinaryHeap<Integer> heap = new MyBinaryHeap<>();

heap.add(68);

heap.add(72);

heap.add(43);

heap.add(50);

heap.add(38);

BinaryTrees.println(heap);

}

运行结果

┌─72─┐

│ │

┌─68─┐ 43

│ │

50 38

remove 方法

• 堆的删除，特指删除堆顶元素
• 步骤
  1. 将 最后一个元素换到根位置，然后删除最后一个元素
  2. 维护堆的性质，将根节点与其两个子节点进行比较，如果根节点 ≥ 两个子节点（假设大顶堆），就不需要再做操作，否则
  3. 如果 当前根节点比两个子节点都大，那么选 Max(左节点， 右节点) 与 根节点 交换，循环，直到两个子节点都比自己小（也包括子节点为空的情况），退出循环
• 上述步骤称为 下滤 siftDown，时间复杂度 O(logn)，因为找子节点不断地 乘以2，在折半次数内会走完整个数组

siftDown 下滤方法

• 首先判断有没有子节点，必须有子节点才进入循环，即必须是 非叶子节点
• 对于完全二叉树，一旦遇到第一个叶子节点，那么它之后的节点（编号比他大的节点）全部都是叶子节点
  • i ＜ 第一个叶子节点的索引
  • 第一个叶子节点的索引 = 非叶子节点的数目 => floor(n / 2)
  • 补充：叶子节点的数目为 floor((n + 1) / 2)
• 一旦进入循环，说明有子节点
  • 左子节点：一定存在
  • 右子节点：不一定存在

/**

* 对目标索引位置的元素进行下滤操作

*

* @param index 目标索引

*/

private void siftDown(int index) {

E element = elements[index];

// 当 Index 位置的节点有子节点，是非叶子节点，就进入循环

// index < 第一个叶子节点的索引，第一个叶子节点的索引=非叶子节点的数目=floor(n / 2)

int notLeafNum = size >> 1;

while (index < notLeafNum) {

// 一定有左子节点,不一定有右子节点 2*index + 2

// 默认以左子节点作为子节点

int childIndex = (index << 1) + 1;

// 检查右节点是否存在，如果存在，比大小，如果右节点的值 > 左节点的值，那么用右节点（选择左右节点中较大的那个）

int rightIndex = childIndex + 1;

if (rightIndex < size && compare(elements[rightIndex], elements[childIndex]) > 0) {

childIndex = childIndex + 1;

}

// 获取较大子节点元素

E childElement = elements[childIndex];

// 如果 新元素 >= 子节点 退出循环

if (compare(element, childElement) >= 0) break;

// 子节点 > 新元素 交换

elements[index] = childElement;

index = childIndex;

}

elements[index] = element; // 一开始根上的那个元素一直被换到之后合适的位置上

}

remove 方法实现

@Override

public E remove() {

emptyCheck(); // 堆为空检查，检查 size 是否为0，如果为0抛出一个异常

E oldRoot = elements[0];

// elements[0] = elements[size - 1]; // 用最后一个元素覆盖根

// elements[size - 1] = null; // 删除最后一个元素

// size--;

elements[0] = elements[--size]; // 用最后一个元素覆盖根

elements[size] = null;

siftDown(0); // 从根下滤

return oldRoot; // 返回被删除的堆顶元素

}

• 测试
  • 首先构建一个最大二叉堆
  • 然后删除堆顶元素

构建一个最大二叉堆

public static void main(String[] args) {

MyBinaryHeap<Integer> heap = new MyBinaryHeap<>();

heap.add(68);

heap.add(72);

heap.add(43);

heap.add(50);

heap.add(38);

heap.add(10);

heap.add(90);

heap.add(65);

BinaryTrees.println(heap);

}

结果

┌───90──┐

│ │

┌─68─┐ ┌─72─┐

│ │ │ │

┌─65 38 10 43

│

50

尝试删除堆顶元素 {12}

public static void main(String[] args) {

MyBinaryHeap<Integer> heap = new MyBinaryHeap<>();

heap.add(68);

heap.add(72);

heap.add(43);

heap.add(50);

heap.add(38);

heap.add(10);

heap.add(90);

heap.add(65);

heap.remove(); // 删除堆顶

BinaryTrees.println(heap);

}

删除堆顶后的结构

┌───72──┐

│ │

┌─68─┐ ┌─50─┐

│ │ │ │

65 38 10 43

replace 方法

删除堆顶元素的同时，插入一个新元素

1. 用新元素替换根节点
2. 对根节点进行下滤

@Override

public E replace(E element) {

elementNotNullCheck(element);

E oldRoot = null;

if (size == 0) { // 如果堆为空，那么直接添加即可

elements[size++] = element;

} else {

oldRoot = elements[0];

elements[0] = element; // 替换堆顶

siftDown(0); // 堆顶下滤

}

return oldRoot;

}

测试

public static void main(String[] args) {

MyBinaryHeap<Integer> heap = new MyBinaryHeap<>();

heap.add(68);

heap.add(72);

heap.add(43);

heap.add(50);

heap.add(38);

heap.add(10);

heap.add(90);

heap.add(65);

BinaryTrees.println(heap);

Integer oldRoot = heap.replace(70);

System.out.println("oldRoot = " + oldRoot);

BinaryTrees.println(heap);

}

运行结果

┌───90──┐

│ │

┌─68─┐ ┌─72─┐

│ │ │ │

┌─65 38 10 43

│

50

oldRoot = 90

┌───72──┐

│ │

┌─68─┐ ┌─70─┐

│ │ │ │

┌─65 38 10 43

│

50

最大堆——批量建堆（Heapify）

给定一堆数据，例如数组，一堆乱七八糟的数，将这些数据按照堆的性质快速构建成一个堆

• 两种做法
  • 自上而下上滤
    • 从根节点往下逐个上滤
    • 每一次上滤就会构建出一个小的最大堆
  • 自下而上下滤
    • 从数组末尾往前逐个下滤
    • 每一次下滤就构建出一个小的最大堆

自上而下上滤

• 上滤就是找自己的爹，根节点没爹，所以可以从 索引1 开始

for (int i = 1; i < size; i++) {

siftUp(i);

}

自下而上下滤

• 下滤就是跟自己的子节点比，叶子节点没有子节点，所以从 第一个叶子节点索引 - 1 开始

for (int i = (size >> 1) - 1; i >= 0; i--) {

siftDown(i);

}

效率对比

• 自上而下上滤
  • 基本等效于挨个添加
• 自下而上下滤 *
  • 不断地先将左右子树变成堆
• 结论：一般情况下自下而上下滤效率高
  • 上滤：让每个节点上滤跑到根部，
  • 下滤：让每个节点下滤跑到叶子节点去
  • 对于完全二叉树，显然接近根的层节点少，远离根的层节点多，那么当然下滤更占优势

复杂对对比

方法	复杂度	本质
自上而下上滤	O(nlogn)	所有节点的深度和
自下而上上滤	O(n)	所有节点的高度和

• 深度值和

  • 对于完全二叉树，仅仅是叶子节点，数目就接近 n/2 个，而且每一个叶子节点的深度都是 O(logn) 级别的，因此仅仅是叶子节点部分，就已经是 O(n/2 logn) = O(nlogn) 了
  • 在 O(nlogn) 的复杂度下，其实已经可以利用经典排序算法对节点进行全排序，理想快排、归并排序

• 高度值和

  • 假设是满二叉树，节点总数为 n，树高为 h，那么 n = 2^h - 1
  • 所有节点的高度之和

$$\begin{gathered} H(n)=2^0\ast (h-0)+2^1\ast (h-1)+2^2\ast (h-2)+...+2^{h-1}\ast [h-(h-1)] \\ =2n-lo{g}_2(n+1) \\ =O(n) \end{gathered}$$

Heapify 实现

从外部传入一堆数据，这里假设是一个数组

• 实现 heapify() 方法，进行自下而上下滤
• 添加一个构造方法，从外部接收一个数组

/**

* 自下而上批量下滤

*/

private void heapify() {

for (int i = (size >> 1) - 1; i >= 0; i--) {

siftDown(i);

}

}

构造方法修改

public MyBinaryHeap(Comparator<E> comparator) {

this(null, comparator);

}

public MyBinaryHeap(E[] array, Comparator<E> comparator) {

this.comparator = comparator;

// 自下而上下滤

if (array == null || array.length == 0) {

this.elements = (E[]) new Object[DEFAULT_CAPACITY];

} else {

size = array.length;

// 数组深拷贝

int capacity = Math.max(DEFAULT_CAPACITY, array.length);

this.elements = (E[]) new Object[capacity];

for (int i = 0; i < array.length; i++) {

this.elements[i] = array[i];

}

// 深拷贝结束

// 堆化

heapify();

}

}

public MyBinaryHeap(E[] array) {

this(array, null);

}

// 不穿比较器的构造方法，调用一下上面那个构造方法就行了

public MyBinaryHeap() {

this(null, null);

}

测试

public static void main(String[] args) {

Integer[] array = {88, 44, 53, 41, 16, 6, 70, 18, 85, 98, 81, 23, 36, 43, 37};

MyBinaryHeap<Integer> heap = new MyBinaryHeap<>(array);

BinaryTrees.println(heap);

}

运行结果

┌───────98──────┐

│ │

┌───88──┐ ┌──70──┐

│ │ │ │

┌─85─┐ ┌─81─┐ ┌─36─┐ ┌─53─┐

│ │ │ │ │ │ │ │

18 41 16 44 23 6 43 37

TopK 问题

给定 n 个数，找出最大/小的 k 个数（k 远远小于 k）

• 如果使用排序算法进行全排序，需要 O(nlogn) 的复杂度
• 基于二叉堆复杂度可以优化为 O(nlogk)
• 对于 找出 k 个最大数的情况
  • 新建一个小顶堆
  • 扫描 n 个整数
    • 先将遍历到的前 k 个数放入堆中
    • 从 第 k + 1 个数开始，如果大于堆顶元素，就使用 replace 操作（删除堆顶操作，将第 k + 1 个数添加到堆中）
  • 循环完毕，堆中剩下的就是最大的前 k 个数

public static void main(String[] args) {

Integer[] array = {88, 44, 53, 41, 16, 6, 70, 18, 85, 98, 81, 23, 36, 43, 37};

// 最小堆

// MyBinaryHeap<Integer> minHeap = new MyBinaryHeap<>((e1, e2) -> e2 - e1);

PriorityQueue<Integer> minHeap = new PriorityQueue<>((e1, e2) -> e1 - e2);

int topK = 5;

for (int i = 0; i < array.length; i++) {

if (minHeap.size() < 5) { // 前 k 个数进入堆

minHeap.add(array[i]);

} else { // 第 k + 1

if (array[i] > minHeap.peek()) { // 如果遍历元素大于对顶元素

minHeap.poll();

minHeap.add(array[i]);

}

}

}

while (!minHeap.isEmpty()) {

System.out.print(minHeap.poll() + " ");

}

}

运行结果

70 81 85 88 98

优先级队列——Priority Queue

• int size()
• boolean isEmpty()
• void enQueue(E element) 入队
• E deQueue(); 出队
• E front(); 获取队头元素
• void clear(); 清空

不同于普通队列的 FIFO 先入先出，优先级队列是按照 优先级高低 进行出队，比如将优先级高的元素作为 队头 优先出队