Version: Next
并查集算法
Union Find并查集算法的模板度极高
并查集算法的关键在于找到
根节点
Union:将两个元素合并为同一个根节点——union(x, y);Find:找到某个元素的根节点——rootNode find(x);
leetcode题目
- 200.岛屿数量
- 547.朋友圈
引例
- 有两家公司如图所示,可见其中
员工6、员工7没啥关系,不是一家的
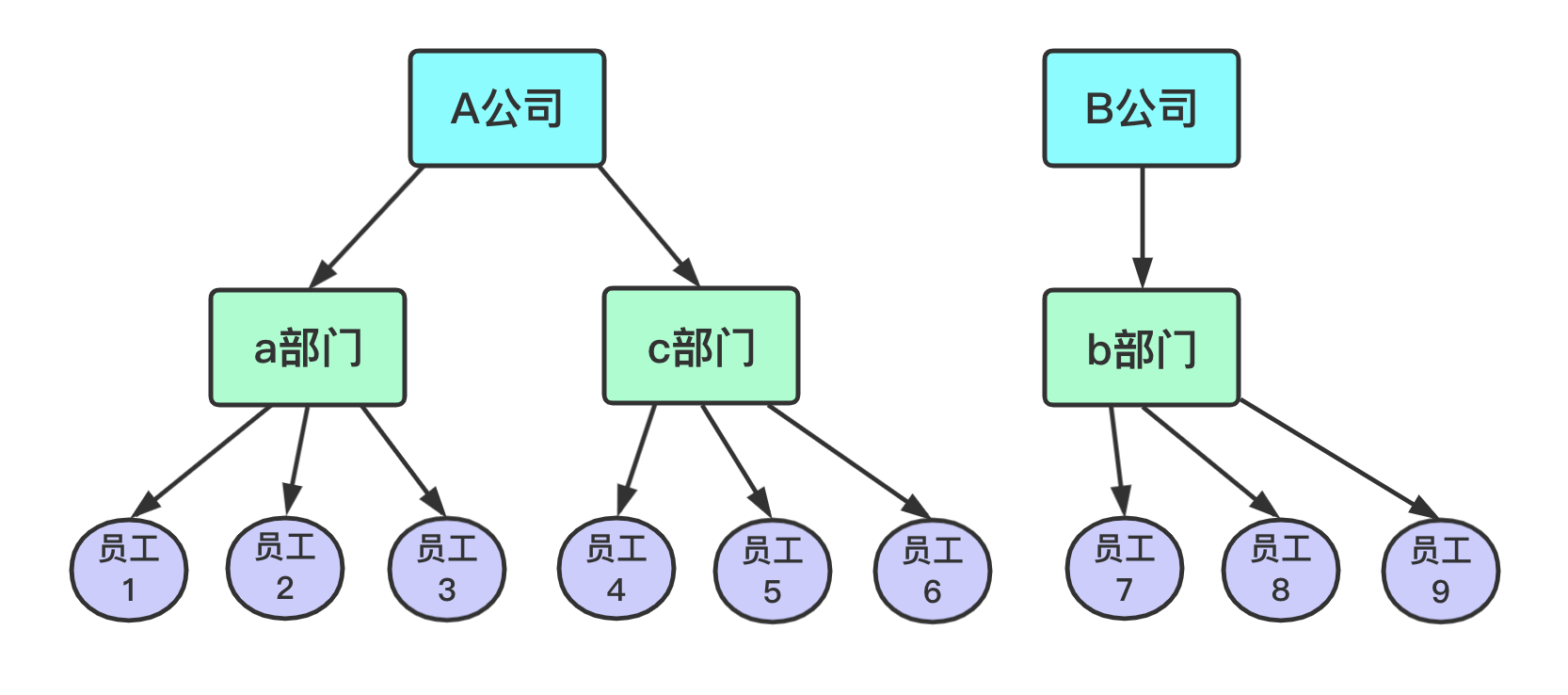
- 有一天,
A公司收购了B公司
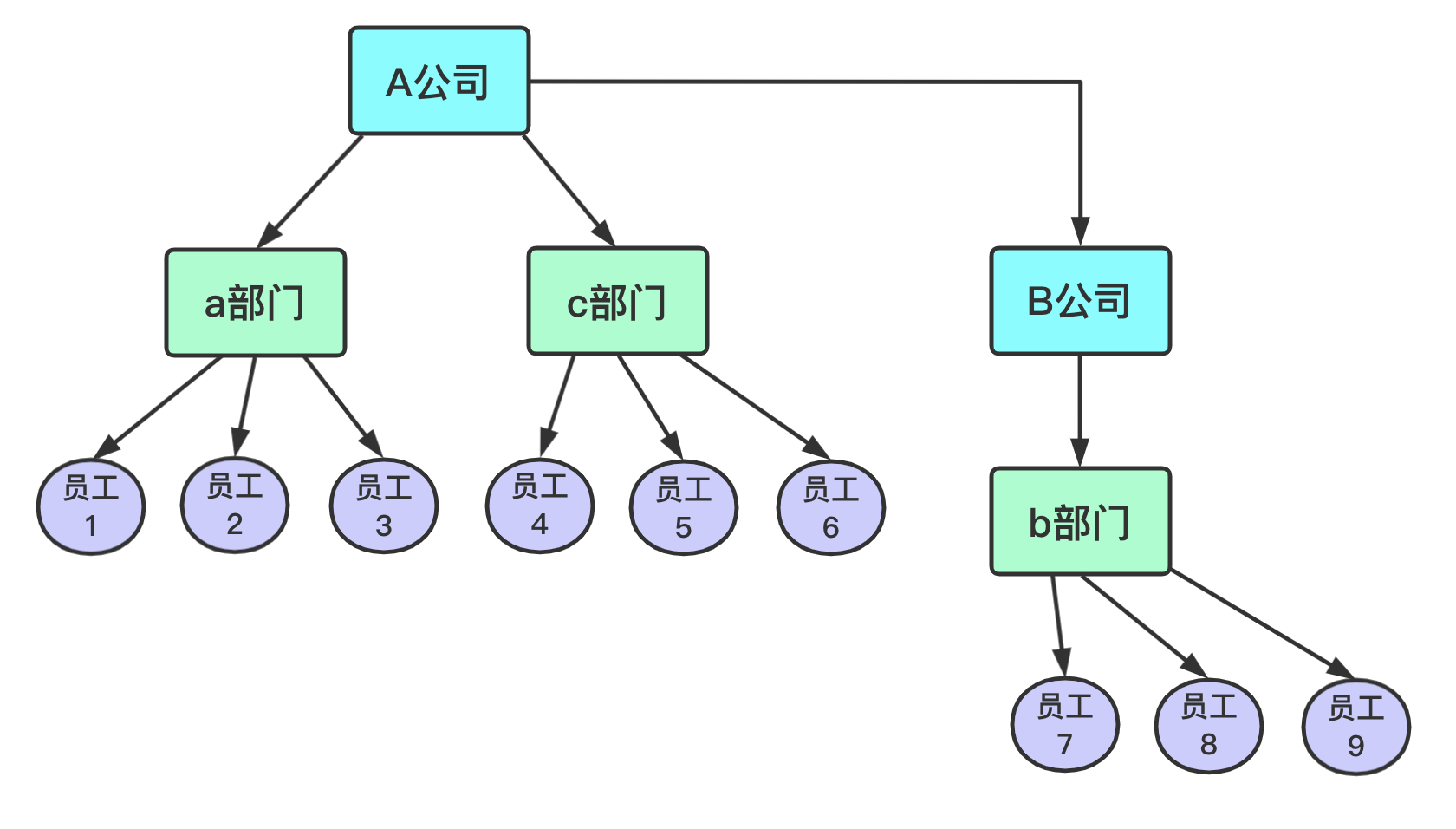
- 此时
员工6和员工7有关系了,他们拥有共同的根——A公司
例
- 根据下图中节点的连接关系,判断给出的组合是否具有相同的
根
组合 是否具有相同的 根(1, 2)√ (0, 7)× (8, 9)√
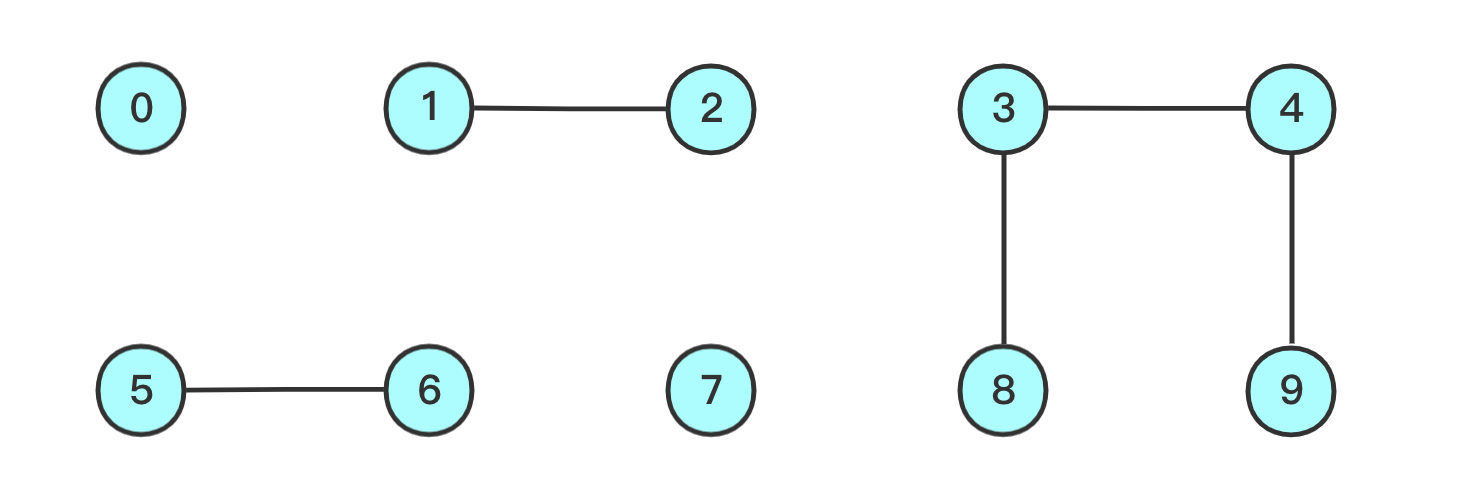
- 添加一些连线
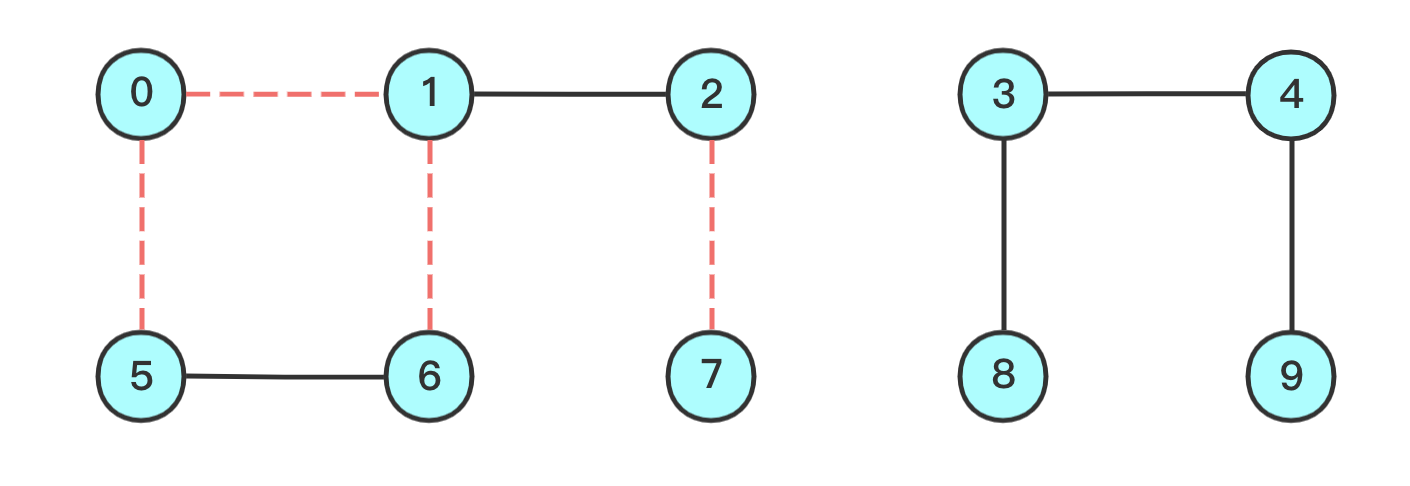
此时,(0, 7)具有相同的根了
编程思想
对于下图,问节点
2、3是否是连着的
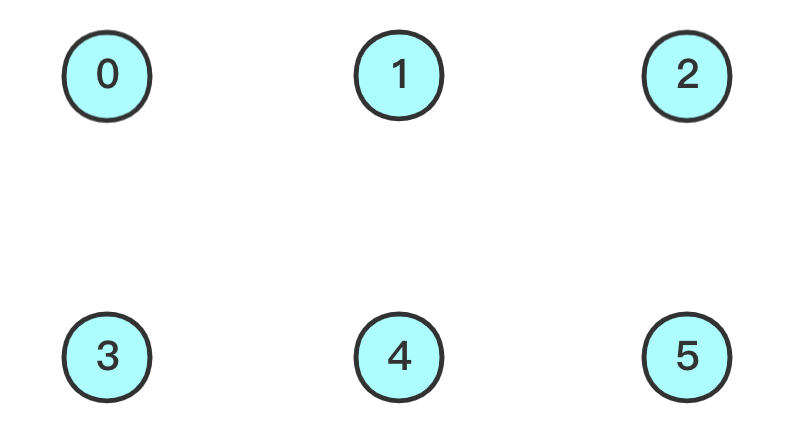
- 根据并查集思想,分别找到
2的根、3的根,如果他们具有相同的根,就是连着的- 使用一个
数组来记录每个节点对应的根节点,是哪个节点用索引标记
节点对应的根节点 0 1 2 3 4 5 数组索引 0 1 2 3 4 5
- 首先要进行
初始化,忽略既定节点连接关系,认为每个节点的根节点就是它自己
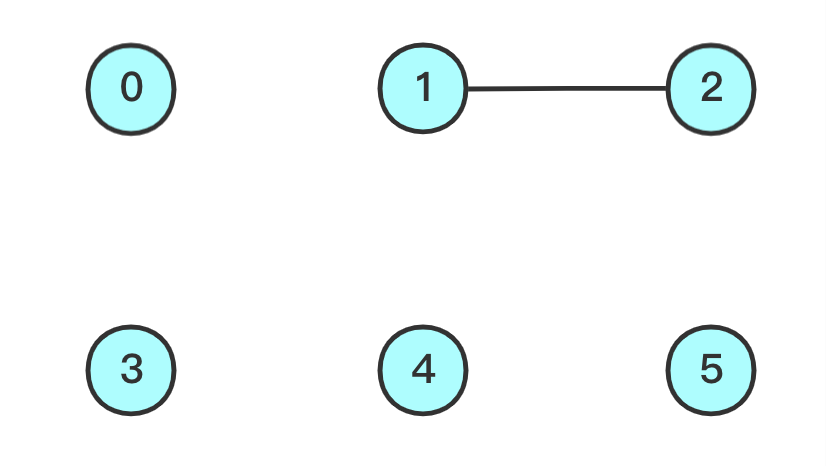
- 人为规定
1为根,之后添加一根线- 此时,
1和2连接,那么2的根应当更新为1
节点对应的根节点 0 1 13 4 5 数组索引 0 1 2 3 4 5
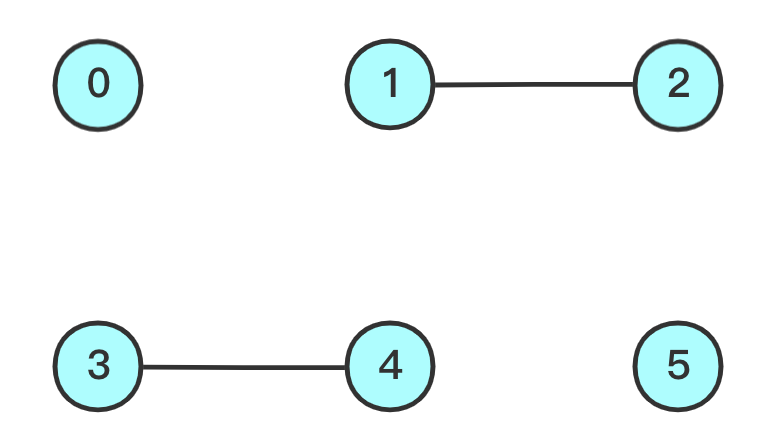
- 添加
3和4的连线- 此时更新
4的根为3
节点对应的根节点 0 1 1 3 35 数组索引 0 1 2 3 4 5
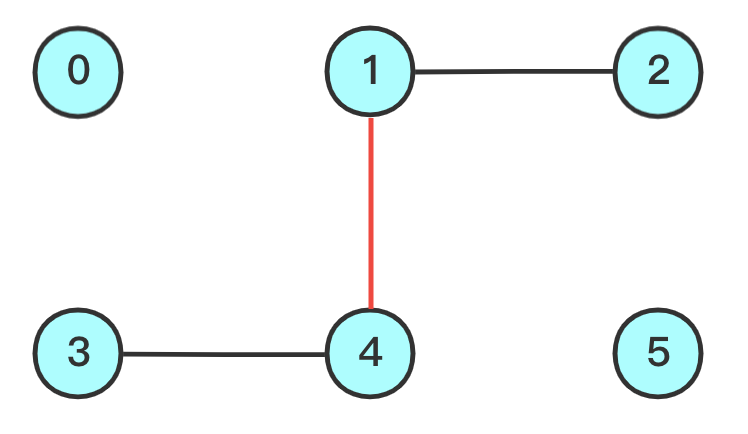
注意
只有数组索引与对应根节点的值 相等了,才说明找到了根,否则要根据当前的"根",继续往上找
- 添加
1和4之间的连线- 此时
4的根是3,不等于根1,于是顺着3去查看3的根- 此时
3的根是3,应当修改3的根为1
节点对应的根节点 0 1 1 修改为 135 数组索引 0 1 2 34 5
此时,检查
2和3是否具有相同的根
节点对应的根节点 0 1 1 1 3 5 数组索引 0 1 234 5
如何查看根
根据下图的搜索方式,可以确定2和3具有相同的根

模板
class UnionFind {
private int[] root = null; // 维护根节点数组
// ...
public UnionFind(...) {
// ...
root = new int[row * col];
for (int i = 0; i < row * col; i++)
root[i] = i; // 初始化,每个节点的根就是自己
}
// Find the root of x
public int find(int x) {
if (x == root[x]) {
return root[x]; // 索引 和 元素 相等,是真正的根
}
return ... find(root[x]); // 不相等,就递归查找
}
// Union two elements into one root
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) { // 两个根不相等,就合并
root[rootX] = rootY;
// ,,,
}
}
}
并查集优化
并查集分为
Union和Find,针对这两个部分,有各自的优化
Quick FindQuick Union
Quick Find
目的就是快速找到一个节点的
根
有如下节点图,及其对应的数组
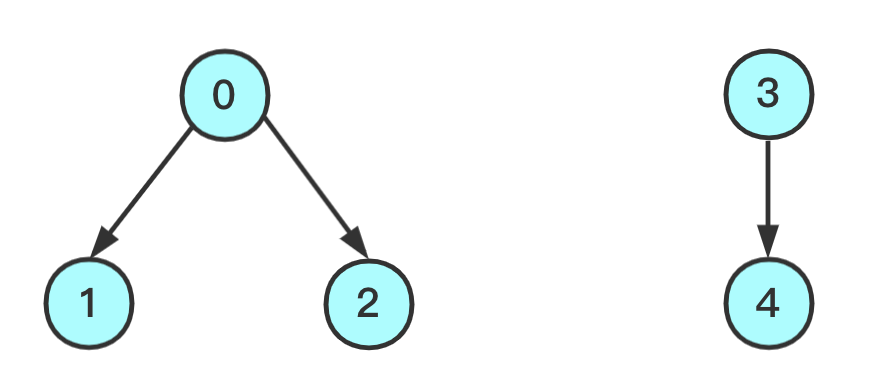
| 节点对应的根 | 0 | 0 | 0 | 3 | 3 |
|---|---|---|---|---|---|
| 索引(节点) | 0 | 1 | 2 | 3 | 4 |
此时,连接2和4
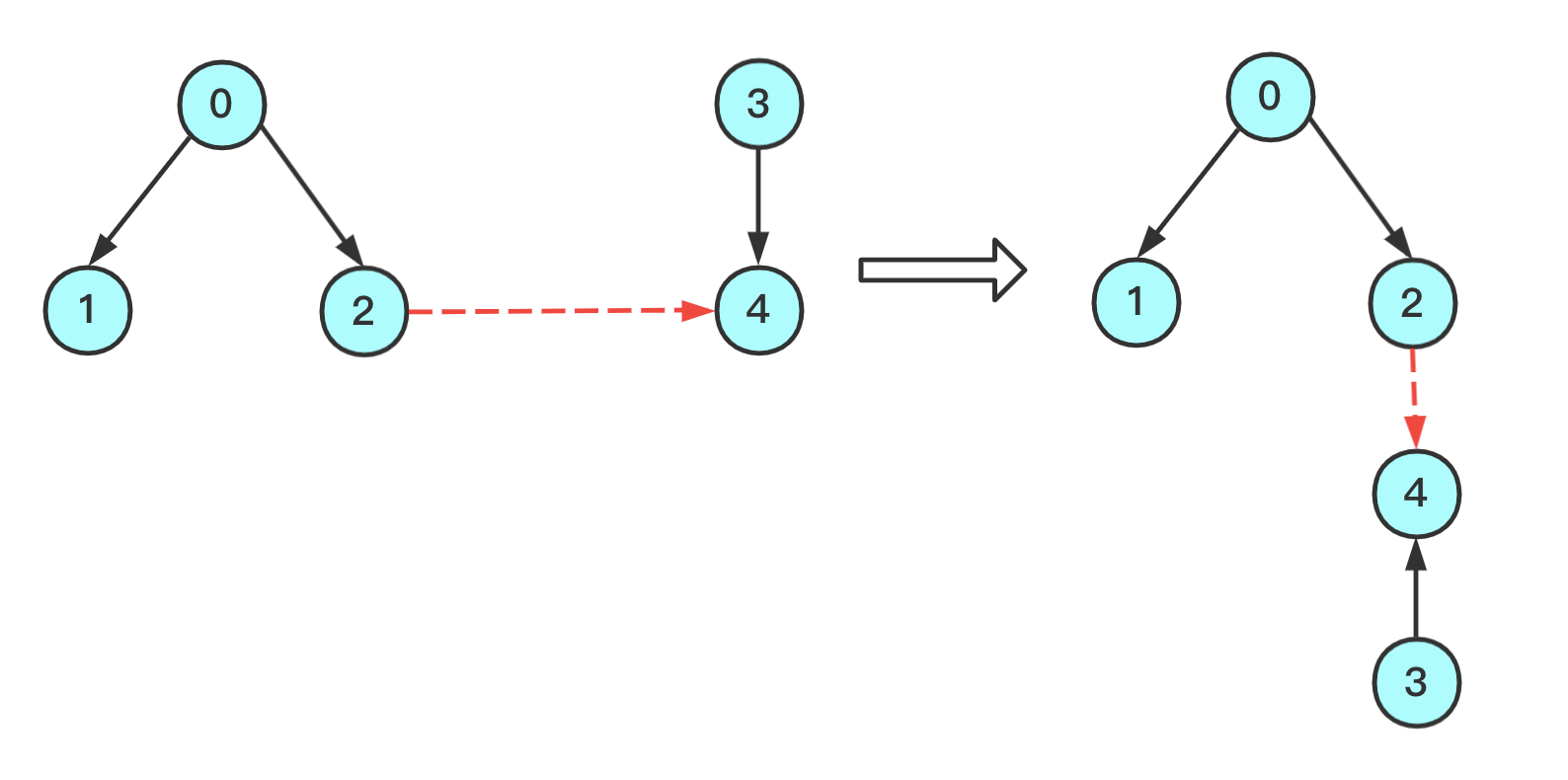
更新数组
- 规定
2为2和4之间的根- 从
4出发发现根是3,由于上一条规定了根是2,故去找22的根是0- 修改
3的根为0

问题
可以发现这个过程非常、非常、非常的麻烦!
所以我们要找到一种快速定位根的方法
Quick Find
- 实际上就是在第一次进行上述过程之后,多做一步,将上述过程的其实元素
4的根直接修改为最终结果0,这样,下一次再找4的根时,不需要重复麻烦的搜索过程,直接返回0即可

代码
Quick Find,在调用find时传入了其实元素x,查找完毕后直接修改元素x对应的根为上次调用find方法找到的最终根
class UnionFind {
private int[] root = null; // 维护根节点数组
// ...
public UnionFind(...) {
// ...
root = new int[row * col];
for (int i = 0; i < row * col; i++)
root[i] = i; // 初始化,每个节点的根就是自己
}
// Find the root of x
public int find(int x) {
if (x == root[x]) {
return root[x]; // 索引 和 元素 相等,是真正的根
}
// Quick Find
// Quick Find 把入口元素x的根直接修改
return root[x] = find(root[x]); // 不相等,就递归查找
// Quick Find 把入口元素x的根直接修改
// Quick Find
}
// Union two elements into one root
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) { // 两个根不相等,就合并
root[rootX] = rootY;
// ,,,
}
}
}
Quick Union——权重
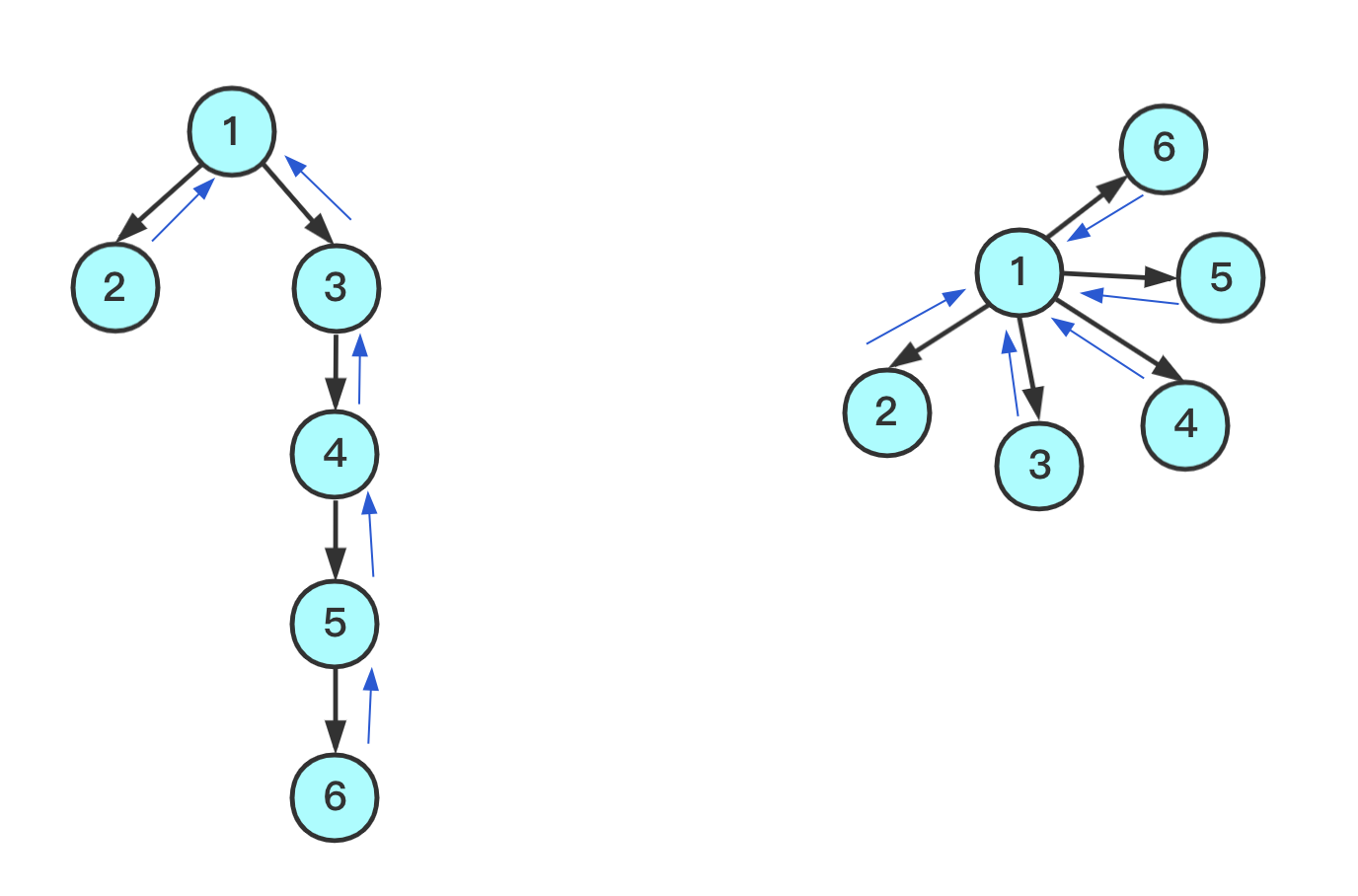
下图所示的两种树状结构,分别找出去节点对应的
根,以找到6的根为例
- 左:需要依次访问
5、4、3- 右:直接到达根
显然,右边的结构找
根更快
权重思路:防止树状结构的
高度太高
比如,将下面两颗树形结构连接起来,直观的做法是将2和3连接
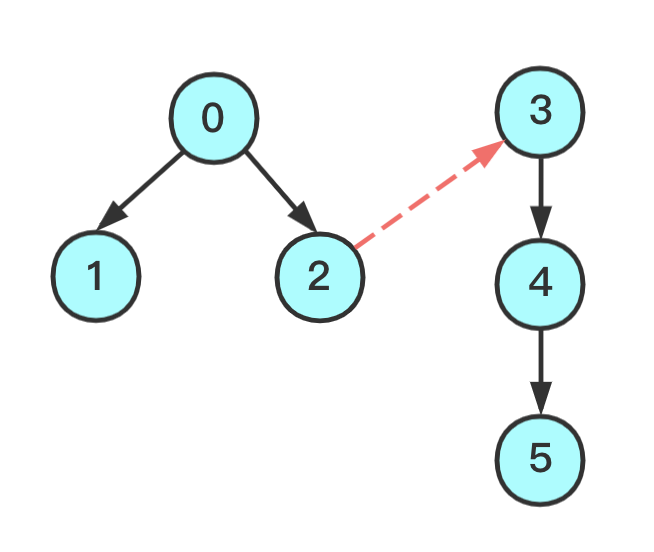
但是这样一来,就会出现上述的问题,所以应当比较权重,在此处,表现为让左边成为右边的子树
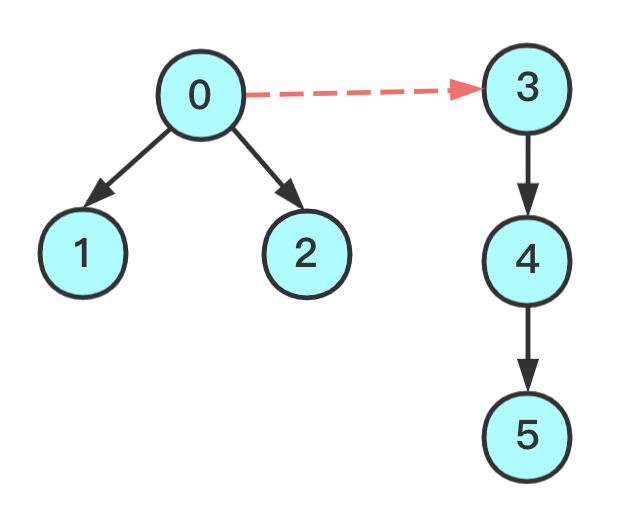
原理
- 比较两个树的高
- 将
高度低的树连接到高度高的树上,使树的高度最低
代码
class UnionFind {
private int[] root = null; // 维护根节点数组
private int[] rank = null; // 树结构的高度
// ...
public UnionFind(...) {
// ...
root = new int[row * col];
rank = new int[row * col];
for (int i = 0; i < row * col; i++) {
root[i] = i; // 初始化,每个节点的根就是自己
rank[i] = 0; // 初始化,高度都为0
}
}
// Find the root of x
public int find(int x) {
if (x == root[x]) {
return root[x]; // 索引 和 元素 相等,是真正的根
}
return root[x] = find(root[x]); // 不相等,就递归查找
}
// Union two elements into one root
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) { // 两个根不相等,就合并
// Quick Union
// Quick Union
if (rank[rootx] > rank[rooty]) { // x 的根权重比y根权重大
root[rooty] = rootx; // 将根更新为权重大的
} else if (rank[rootx] < rank[rooty]) {
root[rootx] = rooty;
} else { // 如果x y 树的权重一样
root[rooty] = rootx; // 把y树 粘到 x树上去
rank[rootx] += 1; // 于是,x的高度+1
}
// Quick Union
// Quick Union
}
}
}