Version: Next
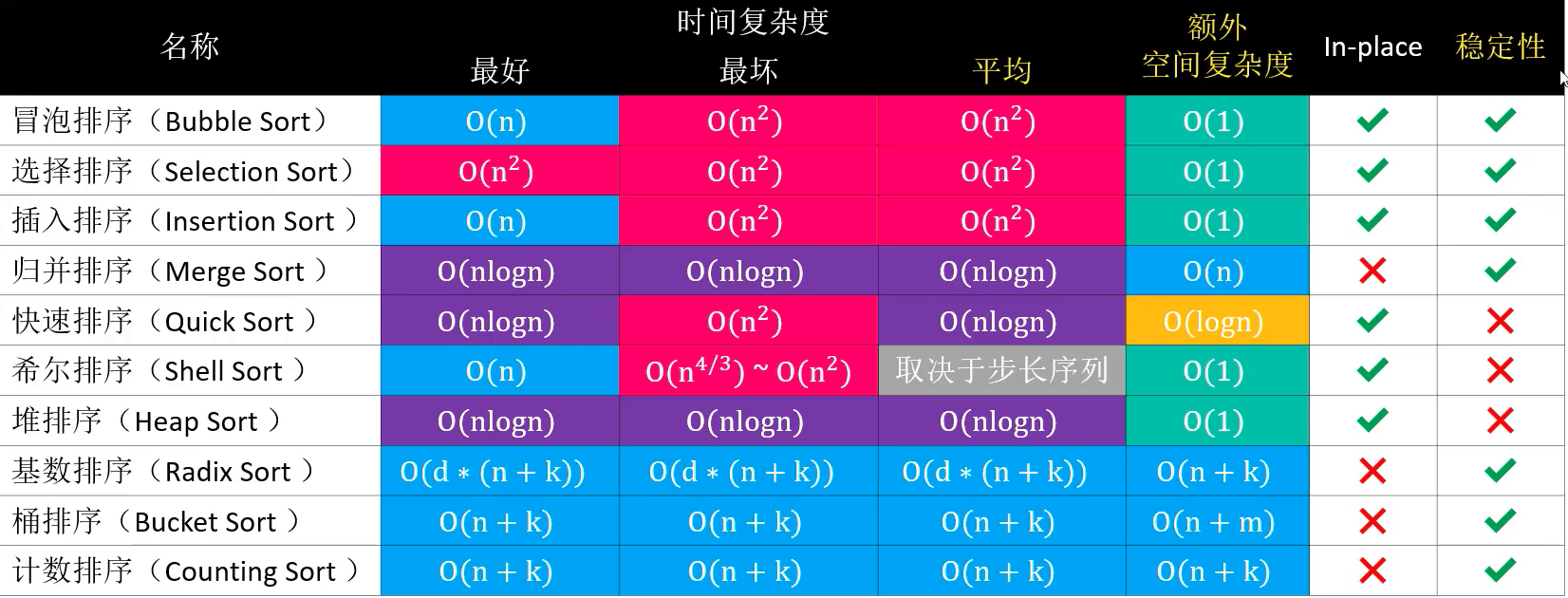
十大排序算法
常见递推式复杂度
| 递推式 | 复杂度 |
|---|---|
| T(n) = T(n/2) + O(1) | O(logn) |
| T(n) = T(n-1) + O(1) | O(n) |
| T(n) = T(n/2) + O(n) | O(n) |
| T(n) = 2 * T(n/2) + O(1) | O(n) |
| T(n) = 2 * T(n/2) + O(n) | O(nlogn) |
| T(n) = T(n-1) + O(n) | O(n^2) |
| T(n) = 2 * T(n-1) + O(1) | O(2^n) |
| T(n) = 2 * T(n-1) + O(n) | O(2^n) |
插入排序
执行流程
- 将整个待排序的序列分为两个部分
- 头部:已经排好序的子序列
- 尾部:顺序乱着的子序列
- 从头扫描每一个元素
- 每当扫描到一个元素,就将它插入到头部合适的位置,使得头部数据依然有序
Sort 抽象类
定义一个排序的抽象类,里面定义一些排序的通用部分
E[] array自身掌握的数组,对它进行排序int cmp(int index1, int index2)比较方法,传入两个元素的下标,进行比较,小于返回负数,等于返回0,大于返回1int cmp(E element1, E element2)比较方法,传入两个元素,进行比较void swap(int index1, int index2)交换两个下标对应的元素abstract sort()排序方法,抽象,延迟到子类实现,取决于不同的排序方法
排序抽象类
public abstract class Sort<E extends Comparable<E>> {
E[] array;
public Sort() {
}
public Sort(E[] array) {
this.array = array;
}
public abstract void sort();
int cmp(int index1, int index2) {
return this.array[index1].compareTo(this.array[index2]);
}
int cmp(E element1, E element2) {
return element1.compareTo(element2);
}
void swap(int index1, int index2) {
E temp = this.array[index1];
this.array[index1] = this.array[index2];
this.array[index2] = temp;
}
public void show() {
for (E e : this.array) {
System.out.print(e + " ");
}
}
}
实现
插入排序
public class InsertionSort<E extends Comparable<E>> extends Sort<E> {
public InsertionSort(E[] array) {
this.array = array;
}
@Override
public void sort() {
for (int begin = 1; begin < this.array.length; begin++) { // 从尾部的第一个元素开始,插入排序
int current = begin;
while (current > 0 && cmp(current, current - 1) < 0) { // 尾部第一个和头部最后一个比,如果尾部第一个比头部最后一个小,就交换
swap(current, current - 1);
// 一旦发生交换, current要左移1位
current--; // 递减考虑下标越界,反映在 while语句的前半部分
}
}
}
public static void main(String[] args) {
Integer[] array = {1, 3, 5, 2, 4};
InsertionSort<Integer> integerInsertionSort = new InsertionSort<>(array);
integerInsertionSort.sort();
integerInsertionSort.show();
}
}
逆序对—— Inversion
例子:
{2,3,8,6,1}逆序对:<2,1> , <3,1>, <8,6>, <8,1>, <6,1>
- 插入排序的时间复杂度,与逆序对的数目成正比
- 逆序对越多,时间复杂度越大
- 逆序对达到最大,最坏时间复杂度 O(n^2)
- 理想时间复杂度 O(n)
- 逆序对很少时,性能非常好,理想情况下甚至可以吊打快速排序
- 数量不是很大是效率也不错
优化
思路
将 交换 改变为 挪动
- 现将待插入的元素备份
- 头部有序序列中,比待插入元素大的,都朝尾部移动 1 位
- 将待插入元素放入最终合适的位置
基于挪动的插入排序
@Override // 优化插入排序
public void sort() {
for (int begin = 1; begin < array.length; begin++) {
// 备份
int current = begin;
E temp = array[current];
// 直接用元素进行比较
while (current > 0 && cmp(temp, array[current - 1]) < 0) {
array[current] = array[current - 1]; // 挪动
current--;
}
array[current] = temp;
}
}
优化——使用二分搜索
排序的大概率套路
- 双指针双向扫描
- 三指针,复制数组扫描
选择排序
- 每一轮,选出剩余元素中的
最大值与当前末尾元素进行交换
public void sort() {
for (int end = arr.length - 1; end > 0; end--) {
int maxIndex = 0;
for (int begin = 1; begin <= end; begin++)
maxIndex = arr[maxIndex] >= arr[begin] ? maxIndex : begin;
swap(maxIndex, end);
}
}