Version: Next
Josephus Problem——约瑟夫问题
假设有8个人,每数3个数就干掉对应的人,
被干掉的人不再数,只数活着的
- 第一次干掉3
- 第二次干掉6
- 第三次干掉1
- ... 直到7,最后一个人,活下来
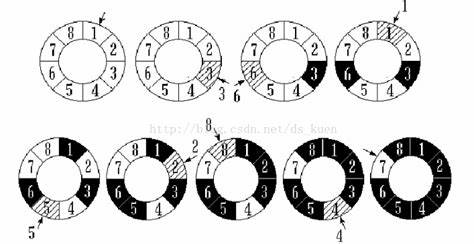
题目:得出节点被干掉的顺序,并给出最后存活的节点
思路
使用双向循环链表,在链表上移动指定步数,移动到的节点从链表中删除
技巧
增设一个成员变量,三个方法
- 成员变量:
current指向当前节点 - 方法:
reset(),让current重新指向头节点first - 方法:
E next(),让current向后移动一下,也就是current = current.next,返回新的current节点的值 - 方法:
E removeCurrent()删除current指向的节点,删除成功后让current自动指向下一个节点,返回被删除节点的值- 需要写一个
remove(Node<E> node)方法,根据节点删除节点
- 需要写一个
private BiLinkedListNode<E> current; // 指向当前节点
reset()
public void reset() {
current = first;
}
next()
public E next() {
if (current == null) return null;
current = current.next;
return current.element;
}
removeCurrent()
边界情况
- 如果链表中只有一个节点
- 用一个引用记录了当前节点的下一个节点,还是自己
- 将当前节点移除,并将current设置为null
public E removeCurrent() {
if (current == null) return null;
// current的下一个节点记录下来
BiLinkedListNode<E> next = current.next;
E removedElement = remove(current); // 移除当前节点,返回被移除节点的值
if (size == 0) {
current = null;
} else {
current = next; // current 指向 current原本的下一个值
}
return removedElement;
}
环形链表法
static void josephus() {
BiCycleLinkedListJosephus<Integer> list = new BiCycleLinkedListJosephus<>();
// 填充成员
for (int i = 1; i <= 8; i++) {
list.add(i);
}
// 起始current指向头节点
list.reset();
// 只要链表不为空,就移动
while (!list.isEmpty()) {
list.next(); // 走两下
list.next();
// 移除当前节点,并让current向前移动一下
System.out.print(list.removeCurrent() + " -> ");
}
}
public static void main(String[] args) {
josephus();
}
3 -> 6 -> 1 -> 5 -> 2 -> 8 -> 4 -> 7 ->
公式法
公式
f(n, m) = (f(n - 1, m) + m) % n;
递归
public int lastRemaining(int n, int m) {
return (n == 1) ? 0 : (lastRemaining(n - 1, m) + m) % n;
}
非递归
public int lastRemaining(int n, int m) {
int res = 0;
for (int i = 2; i <= n; i++)
res = (res + m) % i;
return res;
}
公式推导
大规模答案 = 小规模答案 向后移动 m 个位置,为了处理越界,添加一个取模
如果假设从编号1开始
统一按照编号从 0 开始编写代码
- 在最后返回答案时 + 1