333.最大BST子树
难度 中等
给定一个二叉树,找到其中最大的二叉搜索树(BST)子树,并返回该子树的大小。其中,最大指的是子树节点数最多的。
二叉搜索树(BST)中的所有节点都具备以下属性:
- 左子树的值小于其父(根)节点的值。
- 右子树的值大于其父(根)节点的值。
注意:
- 子树必须包含其所有后代。
进阶:
- 你能想出 O(n) 时间复杂度的解法吗?
Given the root of a binary tree, find the largest subtree, which is also a Binary Search Tree (BST), where the largest means subtree has the largest number of nodes.
A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties:
The left subtree values are less than the value of their parent (root) node's value. The right subtree values are greater than the value of their parent (root) node's value. Note: A subtree must include all of its descendants.
Follow up: Can you figure out ways to solve it with O(n) time complexity?
示例 1:
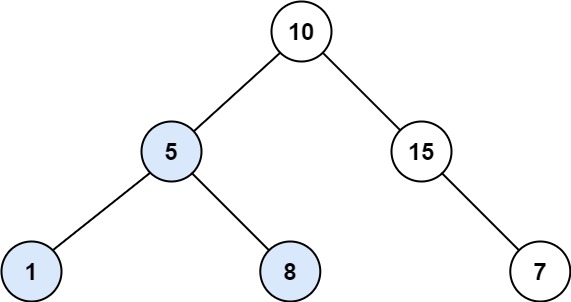
示例 2:
提示:
- 树上节点数目的范围是
[0, 104] -104 <= Node.val <= 104
自顶向下——前序遍历
- 定义方法
func(),返回以 root 为根节点的二叉树的最大BST子树的节点数量- 如果以 root 为根节点的二叉树 S 就是一颗 BST(需要执行判断方法),那么返回 S 的节点数量(需要执行计数方法)
- 否则:递归,返回
func(root.left)和func(root.rignt)中的最大值- 时间复杂度:
- 前序遍历:O(n)
- 判断是否为 BST + 计数:O(2n)
- O(n ^ 2)
自底向上——后序遍历
先判断下方的子树是不是BST,如果不是,则它上侧的都不是BST
获取左子树的最大 BST 信息
获取右子树的最大 BST 信息
一下四种情况说明 root 节点就是以 root 为根节点的二叉树的最大BST子树的根节点
以 root 为根节点,构建BST子树信息
如果以上都不满足,说明最大BST子树不是以 root 为根节点的
- 选左侧最大BST和右侧最大BST中 size 较大的那个
- 如果仅左侧 或 仅右侧存在最大BST,就选存在的那个
定义内部类 Info
- 用来记录 BST 的信息:
- BST 根节点 root
- BST 节点数目 size
- BST 当中的最大值
- BST 当中的最小值
// BST 信息private static class Info {// 根节点public TreeNode root;// 节点数目public int size;// 最大值public int max;// 最小值public int min;public Info() {}public Info(TreeNode root, int size, int max, int min) {this.root = root;this.size = size;this.max = max;this.min = min;}}定义 getInfo(TreeNode root) 方法
- 作用:返回以 root 为根节点的二叉树的 BST 子树信息
- 实现:
计算
li=getInfo(root.left),ri=getInfo(root.right)如果几下条件成立,说明以 root 为根节点的二叉树就是最大 BST 子树
如果
li != null&&ri != null
- 如果
li.size>ri.size,返回 li,否则返回 ri如果
li != null,返回 li,否则返回 ri