Version: Next

654.最大二叉树

654. 最大二叉树

难度中等264收藏分享切换为英文接收动态反馈

给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下：

  1. 二叉树的根是数组 nums 中的最大元素。
  2. 左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树。
  3. 右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树。

返回有给定数组 nums 构建的 最大二叉树 。

You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:

Create a root node whose value is the maximum value in nums.

  • Recursively build the left subtree on the subarray prefix to the left of the maximum value.
  • Recursively build the right subtree on the subarray suffix to the right of the maximum value.
  • Return the maximum binary tree built from nums.

示例 1：

img

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
- 空数组，无子节点。
- [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
- 空数组，无子节点。
- 只有一个元素，所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
- 只有一个元素，所以子节点是一个值为 0 的节点。
- 空数组，无子节点。

示例 2：

img

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

  • 1 <= nums.length <= 1000
  • 0 <= nums[i] <= 1000
  • nums 中的所有整数 互不相同

递归法

  • 遍历数组找到最大值，用最大值创建根节点
  • 设置最大值的左右子节点，递归
public TreeNode constructMaximumBinaryTree(int[] nums) {
if (nums.length == 1) return new TreeNode(nums[0]);
return construct(nums, 0, nums.length);
}
private TreeNode construct(int[] nums, int leftIndex, int rightIndex) {
if (leftIndex == rightIndex) return null;
int maxIndex = leftIndex;
for (int i = leftIndex + 1; i < rightIndex; i++)
if (nums[i] > nums[maxIndex]) maxIndex = i;
TreeNode currentRoot = new TreeNode(nums[maxIndex]);
currentRoot.left = construct(nums, leftIndex, maxIndex);
currentRoot.right = construct(nums, maxIndex + 1, rightIndex);
return currentRoot;
}
public static void main(String[] args) {
int[] nums = {3, 2, 1, 6, 0, 5};
TreeNode treeNode = new _654最大二叉树().constructMaximumBinaryTree(nums);
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(treeNode);
while (!queue.isEmpty()) {
TreeNode head = queue.poll();
System.out.println(head.val);
if (head.left != null)
queue.offer(head.left);
if (head.right != null)
queue.offer(head.right);
}
}

变种题：返回一个数组

返回一个数组，存放的是每个节点的父节点的索引值

  • 没有父节点的话，索引值存 -1
  • 重要技巧，使用 栈

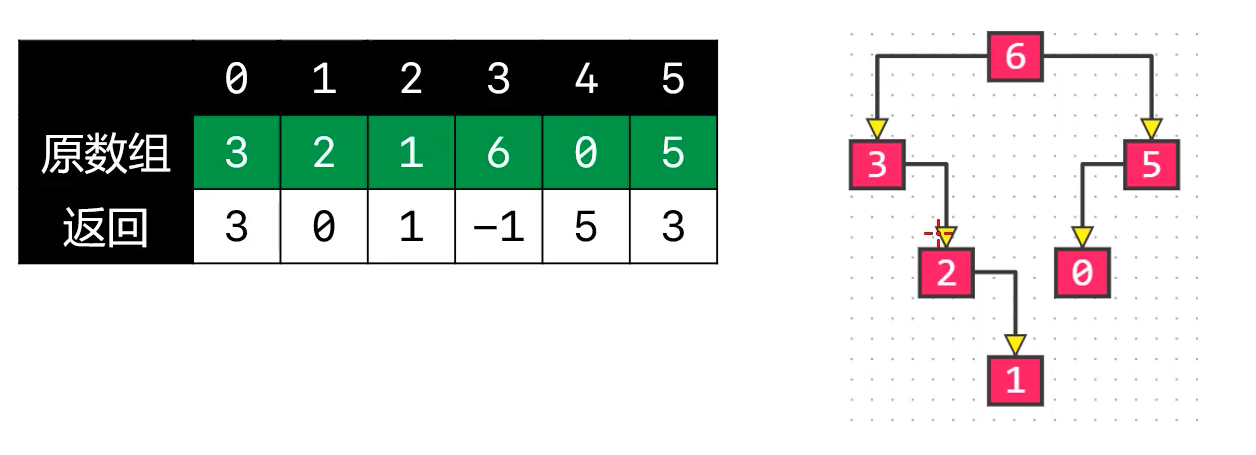
image-20210406144926985

思考：

  • 父节点的特点：元素值比当前自身大
  • 假设从第一个元素 3 开始扫描，那么一定是向右扫描，会发现两个比 3 大的元素 6、5，此时分析可知在数组中离 3 较近的 6 是其父节点
  • 如果不是第一个元素，那么 两边都要扫描，因为不确定当前节点是其父节点的左子树还是右子树
    • 如果在左右两边都找到了 比自己大 的值，那么取其中 较小 的那个
  • 结论：找每一个元素，左边第一个 和 右边第一个 比自己大的元素值，再选出其中元素值较小的那个，就是自己的父节点元素值
技巧

使用 栈，只需要扫描一次数组，就可以得到目标结果

  • 利用栈求左、右第一个比自己大的数

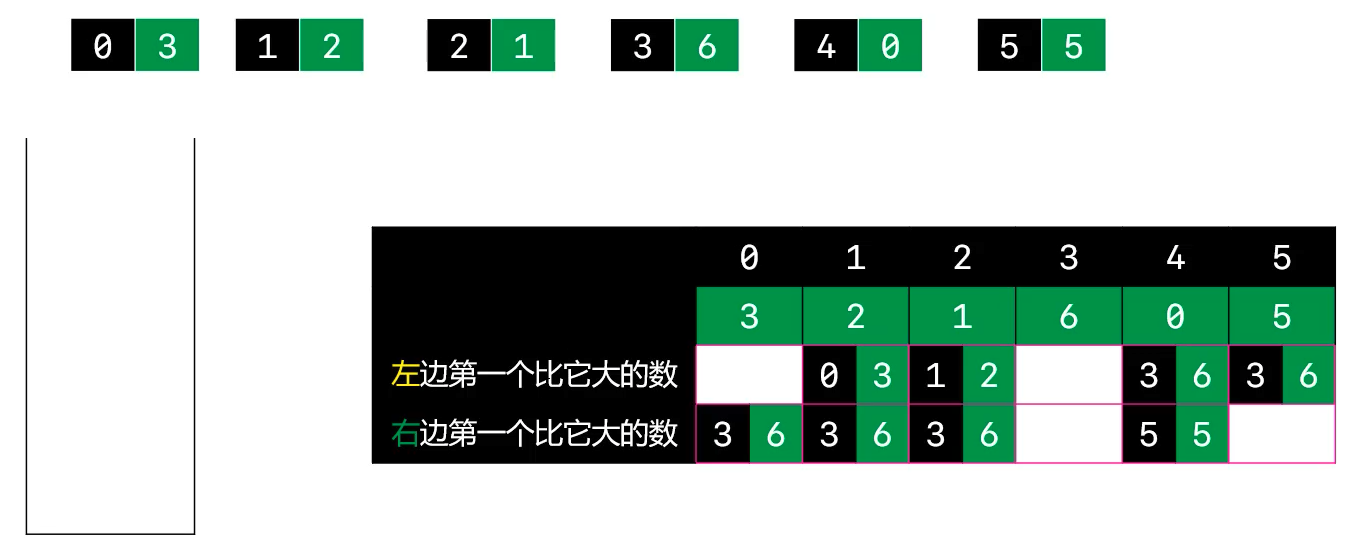
image-20210406151405270

  • 规定从栈底 → 栈顶 元素值单调递减
  • 在即将 push 元素时，比较栈顶与当前元素值
    • 如果当前元素值 小于 栈顶元素：直接入栈，此时原先栈顶元素值就是当前元素值左侧第一个比它大的值
    • while 如果当前元素值 大于 栈顶元素:弹出栈顶元素，此时 弹出的栈顶元素 的右侧第一个比自己大的元素，就是试图如栈的当前元素值
public int[] parentIndexes(int[] nums) {
if (nums == null || nums.length == 0) return null;
int[] res = new int[nums.length];
int[] leftFirstBigger = new int[nums.length];
int[] rightFirstBigger = new int[nums.length];
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < nums.length; i++) {
leftFirstBigger[i] = -1; // 初始化
rightFirstBigger[i] = -1;
while (!stack.isEmpty() && nums[i] > nums[stack.peek()])
rightFirstBigger[stack.pop()] = i;
if (!stack.isEmpty()) leftFirstBigger[i] = stack.peek();
stack.push(i);
}
for (int i = 0; i < leftFirstBigger.length; i++) {
// 注意比的是二者数值中较小的，不是索引较小的
if (leftFirstBigger[i] == -1 && rightFirstBigger[i] == -1)
res[i] = -1;
else if (leftFirstBigger[i] == -1)
res[i] = rightFirstBigger[i];
else if (rightFirstBigger[i] == -1)
res[i] = leftFirstBigger[i];
else
res[i] = nums[leftFirstBigger[i]] < nums[rightFirstBigger[i]] ? leftFirstBigger[i] : rightFirstBigger[i];
}
return res;
}