Version: Next
归并排序
1945 年由冯·诺依曼提出
- 不断的将当前序列平均分割为
2个子序列
- 分割到不能再分割位置,即只剩
1个元素- 不断的将
2个子序列合并为一个有序序列- 直到最终只剩下一个有序序列
innerSort(.., ..) 方法
innerSort(int begin, int end)方法
- 对
[begin, end)范围内的元素进行归并排序- 归并排序是标准分治法,需要设计递归,这是这样一个方法,方便递归的实现
- 递归机:当
end - begin < 2表示序列已经切到只剩下1个元素了,停止切割,开始合并
分割
// 对 [begin, end) 范围内的元素进行归并排序,左闭右开
private void innerSort(int beginIndex, int endIndex) {
if (endIndex - beginIndex < 2) return; // 递归机
// 递归二分
int middleIndex = (beginIndex + endIndex) >> 1; // 除以 2
innerSort(beginIndex, middleIndex); // 左
innerSort(middleIndex, endIndex); // 右
// 合并
merge(beginIndex, middleIndex, endIndex);
}
merge(int begin, int middle, int end) 方法
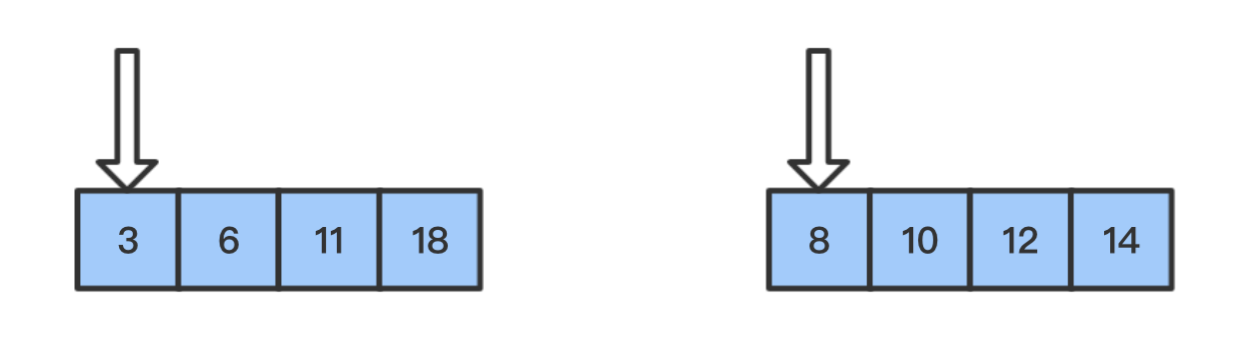
- 采用双指针法
- 每次比较两个指针指向元素的大小
- 将
较小(从小到大排序)元素放到数组的第一个位置- 将
较小元素对应的 指针右移- 直到两个指针都走到头
细节
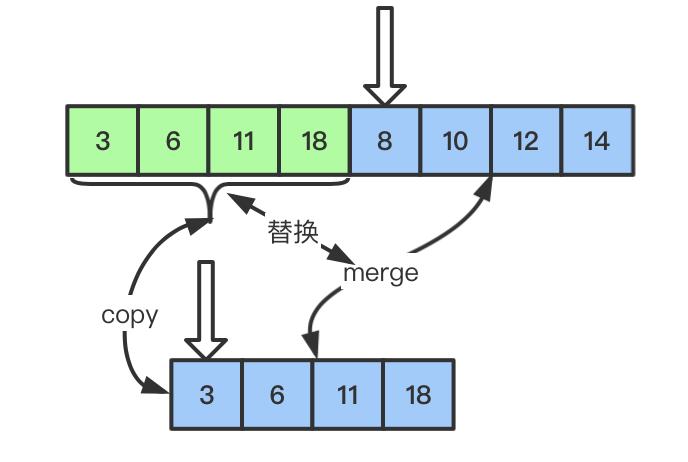
需要 merge 的 2 个子序列在同一数组中,并且彼此相邻
合并之后的有序序列,依然占据原先未合并时的内存空间
- 为了更好的完成合并,需要将其中一组序列先备份,就称为
leftArray
middle - begin,数值上等于array.lengt >> 1- 推荐将左边的备份,即
[begin, middle)
- 因为构建新的大的有序序列,总是从左往右的,所以左侧的元素会先被取代
- 分别给定左右子序列的指针和结尾位置
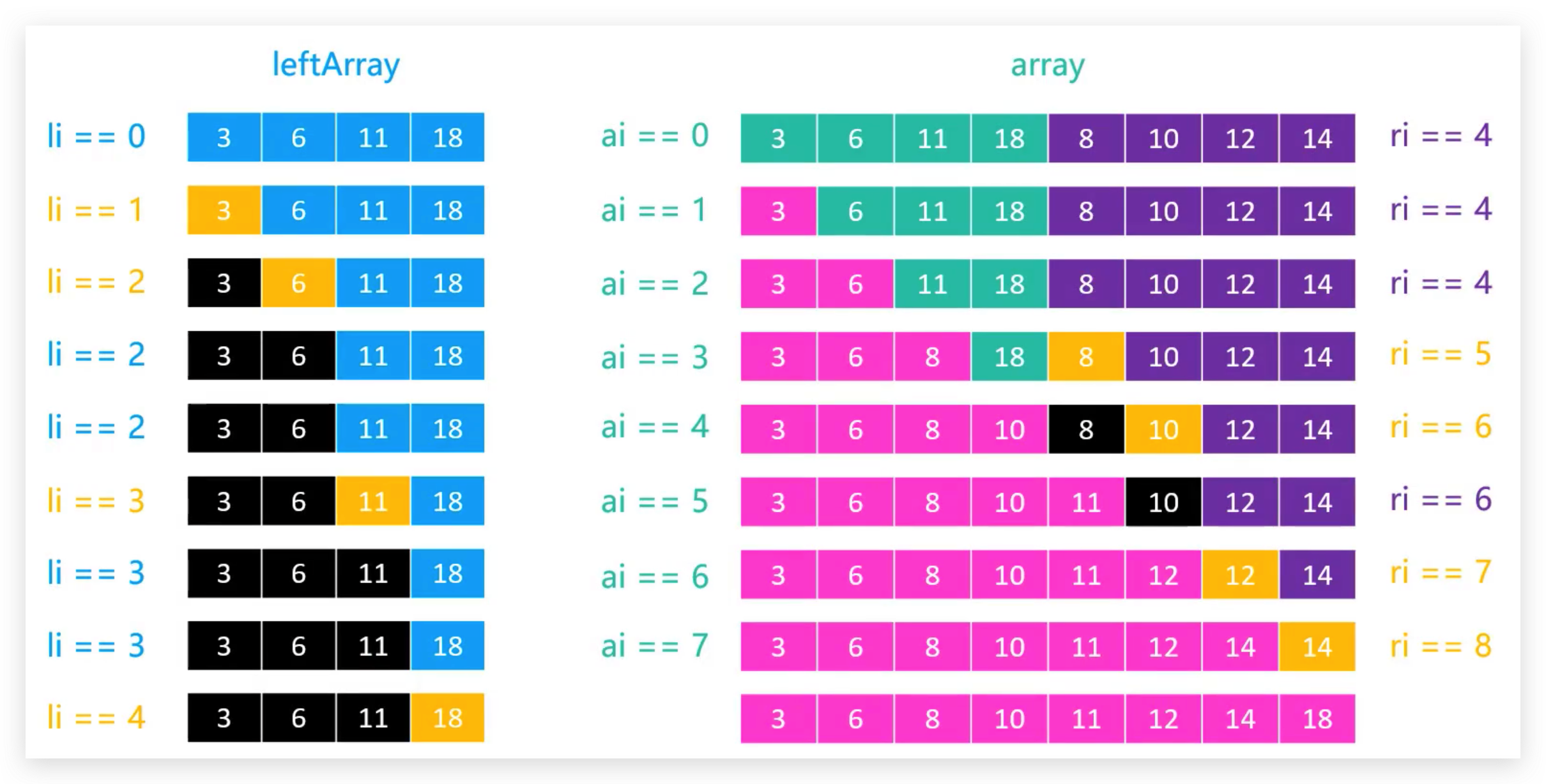
li——左侧指针 初始值0le——左侧结尾位置,数值上等于左侧子序列的长度,根据左闭右开原则,等于mid - beginri——右侧指针,初始值等于middlere——右侧结尾指针,初始值end- 给出下一个即将被覆盖的元素对应的索引
ai,初始值为begin步骤
- 比较
li、ri指向的元素的值
li < ri——li右移,ai右移,ri不动li > ri——ri右移,ai右移,li不动li或ri任意一个先达到了le或re,到头了,那么就可以把对面剩下的元素直接无脑拿来覆盖了
- 左边提前结束:那么直接完事,因为右侧剩下的元素本来就在最终序列的内存位置中
- 右边提前结束:把左边剩下的元素无脑搬运
public class MergeSort<E extends Comparable<E>> extends Sort<E> {
// 左侧数组的备份
private E[] leftArray;
public MergeSort(E[] array) {
// 提前把备份左侧数组在堆中创建出来
this.leftArray = (E[]) new Comparable[array.length >> 1];
this.array = array;
}
@Override
public void sort() {
// 对整个序列进行归并排序
innerSort(0, array.length);
}
// 对 [begin, end) 范围内的元素进行归并排序,左闭右开
private void innerSort(int beginIndex, int endIndex) {
if (endIndex - beginIndex < 2) return; // 递归机
// 递归二分
int middleIndex = (beginIndex + endIndex) >> 1; // 除以 2
innerSort(beginIndex, middleIndex); // 左
innerSort(middleIndex, endIndex); // 右
// 合并
merge(beginIndex, middleIndex, endIndex);
}
// 合并 将 [begin,middle) 和 [middle, end) 合并
private void merge(int begin, int middle, int end) {
int li = 0;
int le = middle - begin;
int ri = middle;
int re = end;
int ai = begin;
// 把左侧数组备份到临时数组中
for (int i = li; i < le; i++) {
this.leftArray[i] = array[begin + i]; // 注意下标应该是 begin+i
}
while (li < le) { // 只要左边还没合并完 (如果左边合并完了,右边直接不用处理)
// li ri 比大小
if (ri < re && cmp(array[ri], leftArray[li]) < 0) // ri不能越界 && 右比左小
array[ai++] = array[ri++];
// 把左元素搬运走
/*array[ai] = leftArray[li];
// li ai 都加1
li++;
ai++;*/
else // 右 >= 左
array[ai++] = leftArray[li++];
// 把右边元素伴奏
/*array[ai] = array[ri];
ri++;
ai++;*/
}
}
public static void main(String[] args) {
Integer[] array = {1, 3, 5, 7, 2, 4};
MergeSort<Integer> mergeSort = new MergeSort<>(array);
mergeSort.sort();
mergeSort.show();
}
}
时间复杂度
O(nlogn)