Version: Next
汉诺塔
编程实现把
A的n个盘子移动到C(盘子编号是[1, n])
- 每次只能移动
1个盘子- 大盘子必须在小盘子下面
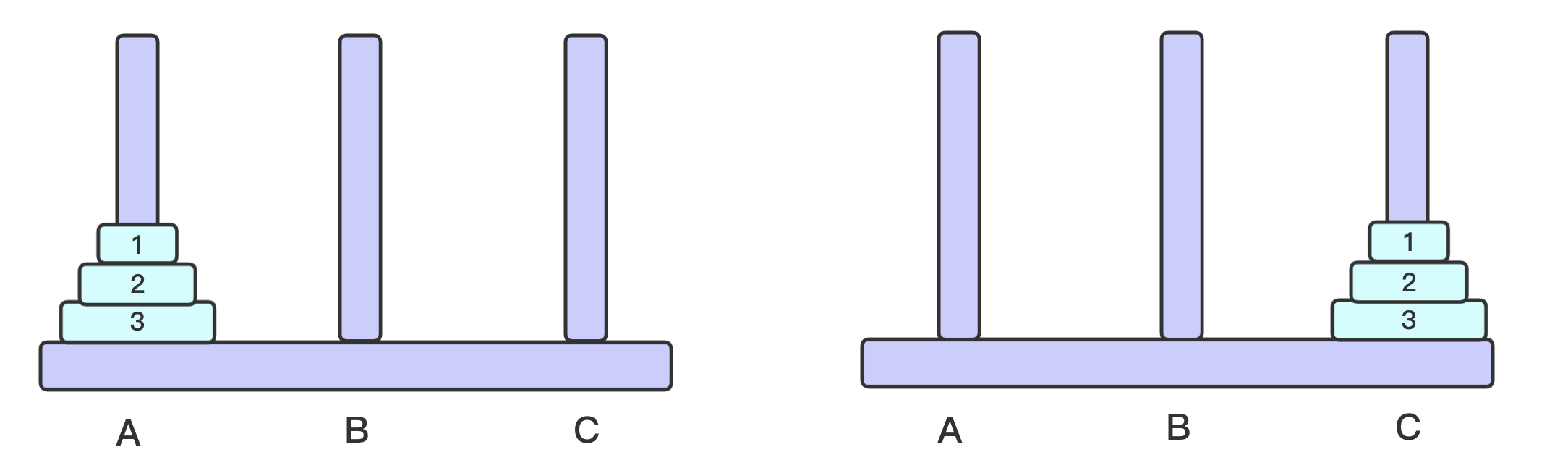
思路:
- 考虑边界情况:
- 共
1个盘子:直接挪过去- 共
2个盘子:1挪到B,2挪到C,1从B挪到C- 共
3个盘子:1挪动到C,2挪动到B,1挪动到B,3挪动到C,1挪动到A,2挪动到C,1挪动到C
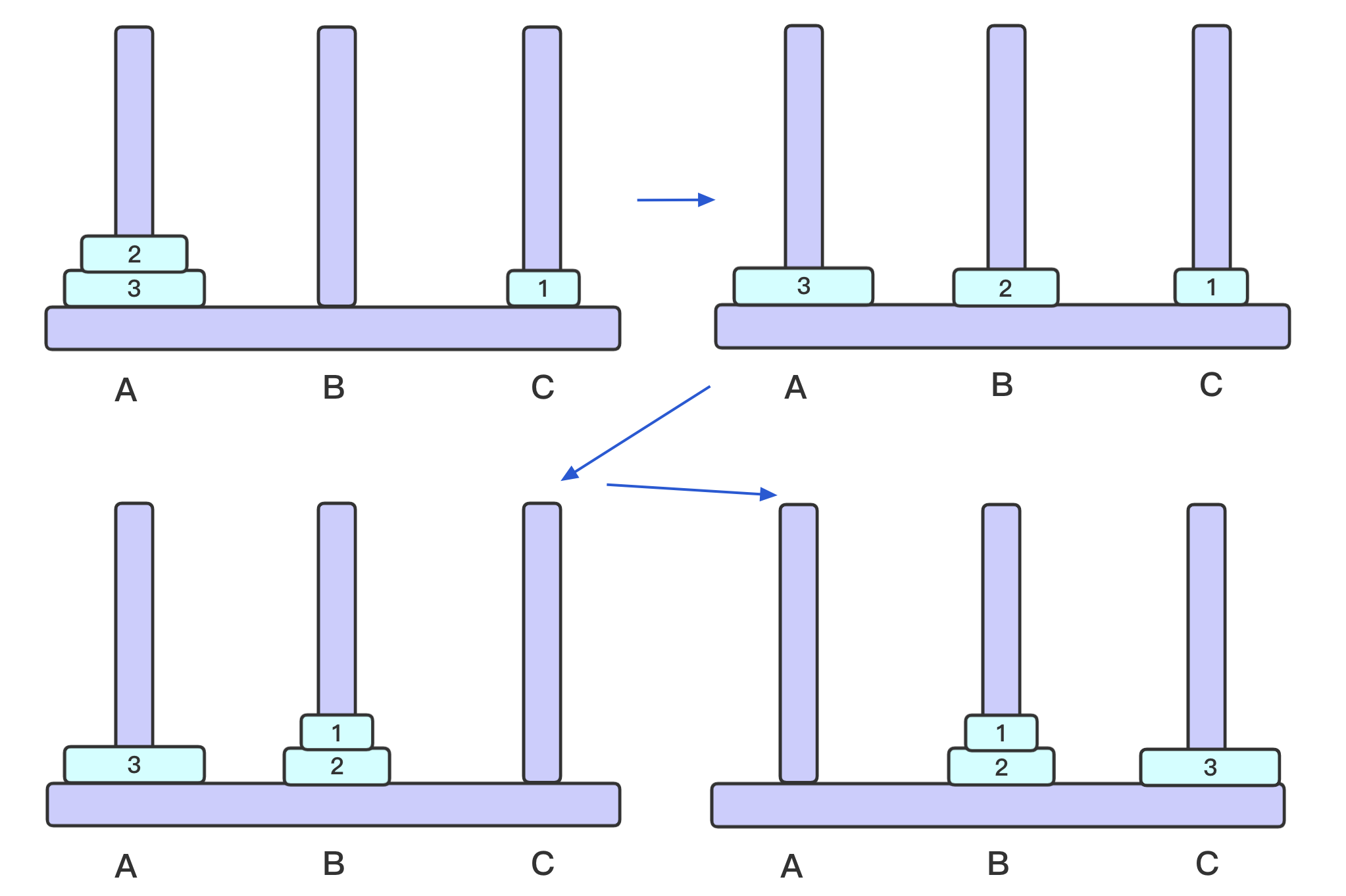
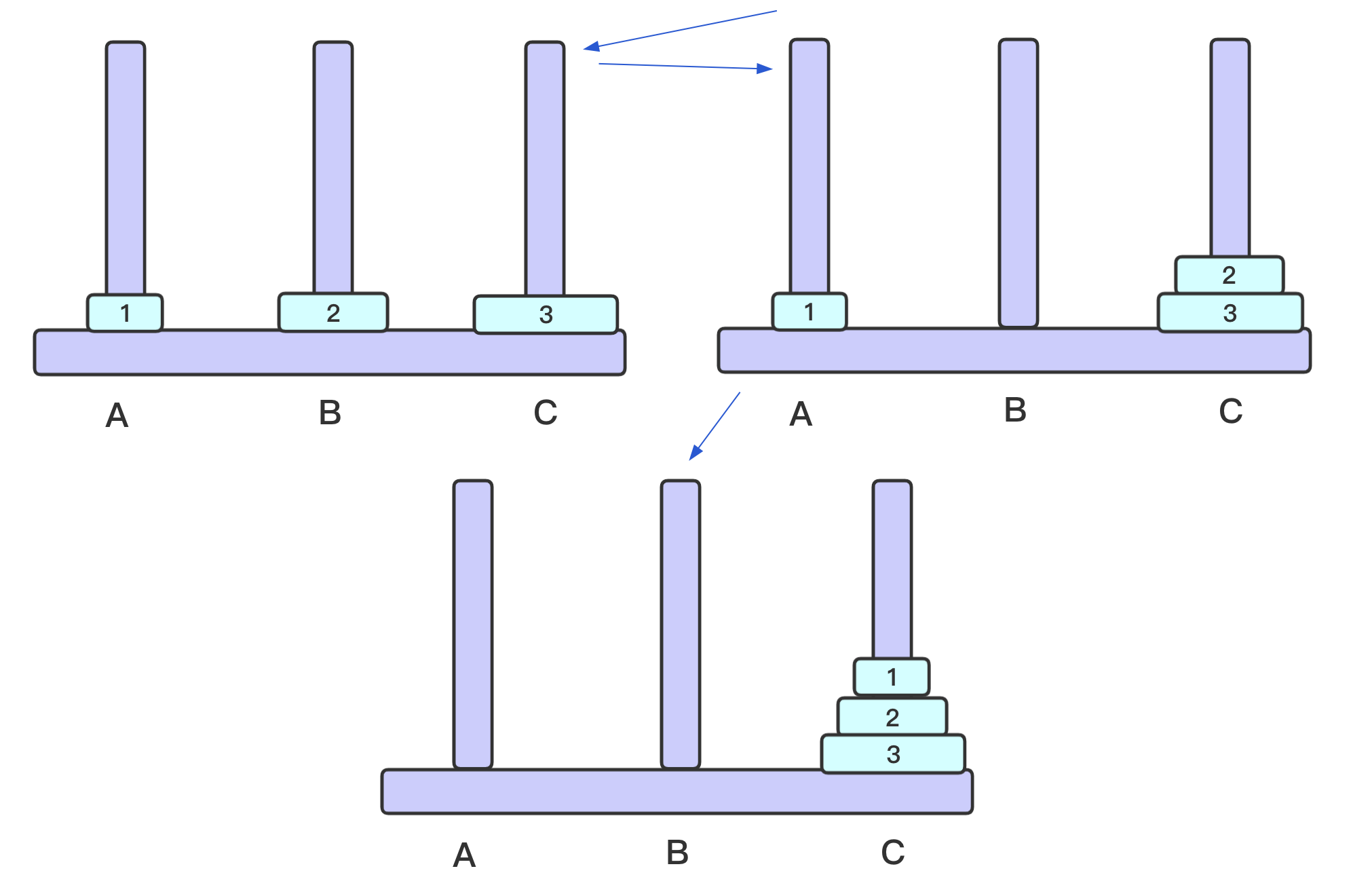
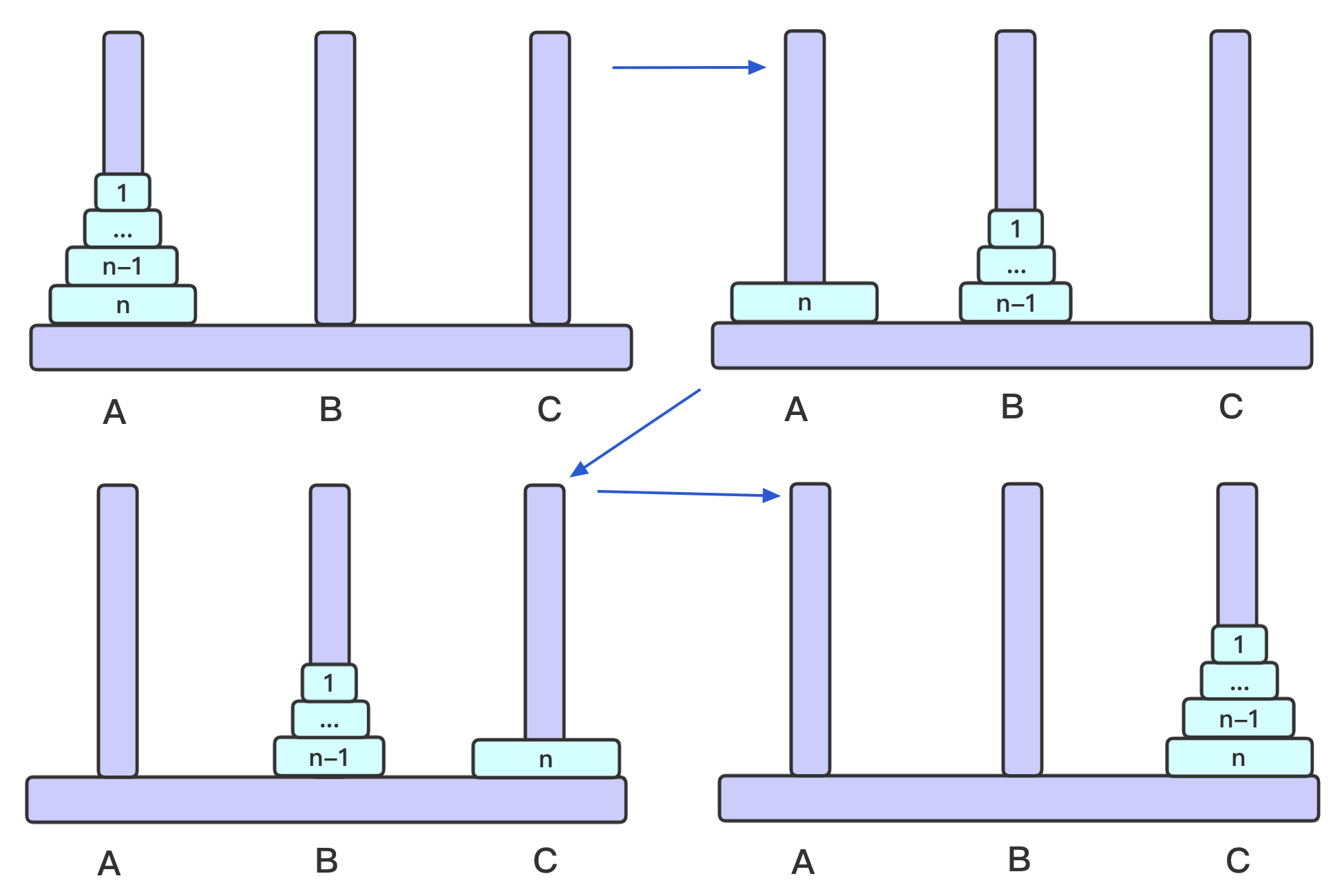
观察递归性
- 选出过程中的两张图,观察一下
- 可以看做是将除了
3之外的盘子,整体移动到B
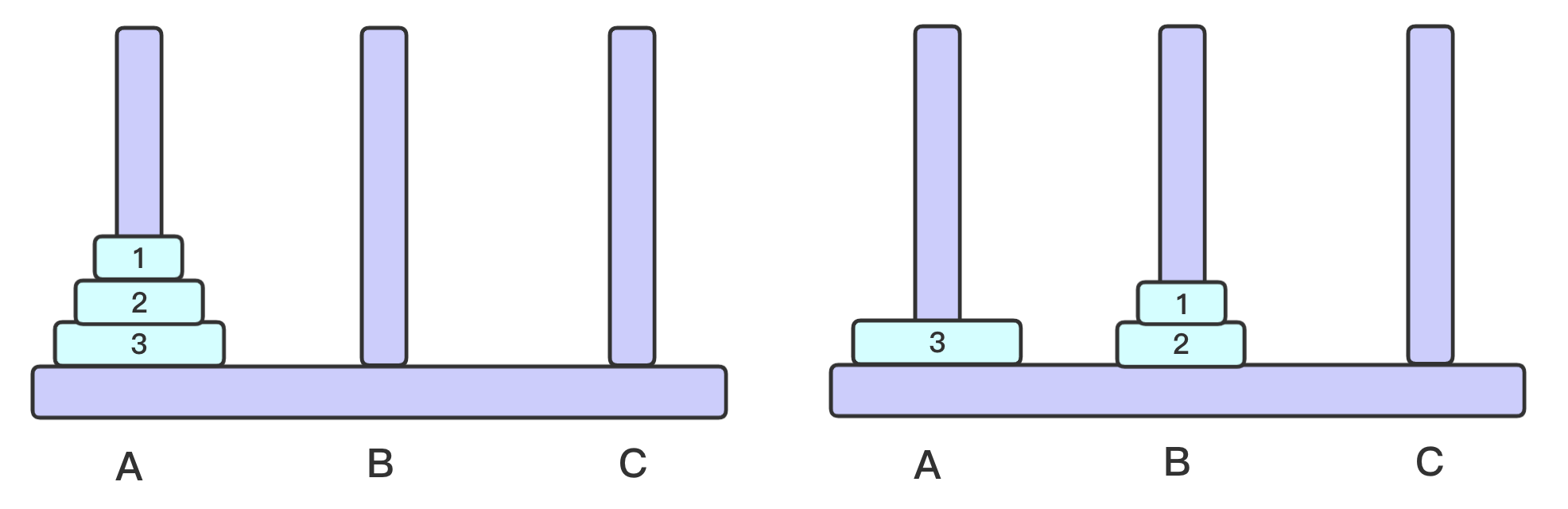
当
n == 1时,直接将盘子从A移动到C当
n > 1时,拆分为3大步骤:
将
n - 1个盘子从A移动到B将
第n个盘子从A移动到C将
n - 1个盘子从B移动到C其中
步骤1和步骤3为递归调用
代码
public class Hanoi {
/**
* 汉诺塔
* 将 n 个盘子,从A移动到C,依次打印每一步执行情况
*
* @param n 盘子数
* @param A 柱子A
* @param B 柱子B
* @param C 柱子C
*/
public void hanoi(int n, String A, String B, String C) {
// 只有一个盘子直接挪动
if (n == 1) {
move(1, A, C);
return;
}
// 一般情况,3步走
// 1. 将n - 1个盘子从 A 移动到 B, 借助 C
hanoi(n - 1, A, C, B);
// 2. 将 第n个 从 A 移动到 C
move(n, A, C);
// 3. 将 n - 1 个盘子从 B 移动到 C , 借助A
hanoi(n - 1, B, A, C);
}
private void move(int element, String from, String to) {
System.out.println("将 " + element +
" 从 [" + from + "] 移动到了 [" +
to + "] ");
}
public static void main(String[] args) {
new Hanoi().hanoi(3, "A", "B", "C");
}
}
运行结果
将 1 从 [A] 移动到了 [C]
将 2 从 [A] 移动到了 [B]
将 1 从 [C] 移动到了 [B]
将 3 从 [A] 移动到了 [C]
将 1 从 [B] 移动到了 [A]
将 2 从 [B] 移动到了 [C]
将 1 从 [A] 移动到了 [C]
时间复杂度
move()为O(1)- 假设
hanoi方法执行消耗的时间为T(n)- 则根据实现代码可推出:
T(n) = T(n - 1) + O(1) + T(n - 1),对应两次n - 1递归,一次move(),合并同类项得到T(n) = 2 * T(n - 1) + O(1)- 继续展开
T(n) = 2 * [2 * T(n - 2) + O(1)] + O(1)=2 * [2 * T(n - 2)] + 2*O(1) + O(1)=2 ^ 2 * T(n - 2) + 2*O(1) + O(1)- 继续展开
2 ^ 3 * T(n - 3) + 2^2*O(1) + O(1)...- 根据极限思想,推出
O(2 ^ n)