Version: Next
5.最长回文子串
难度 中等
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
示例 3:
输入:s = "a"
输出:"a"
示例 4:
输入:s = "ac"
输出:"a"
提示:
1 <= s.length <= 1000s仅由数字和英文字母(大写和/或小写)组成
暴力法
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| a | b | b | a | b | a |
思路
- 找出所有的子串
- 对每个字段判断是不是回文串
- 记录回文串的最大长度
实现
- 双指针 begin 、 end 框选出子串范围
- 列举出所有子串:时间复杂度为 O(n ^ 2)
- 针对每一个子串,检查其是否为回文串,时间复杂度为 O(n)
- 总时间复杂度 O(n ^ 3), 空间复杂度 O(1)
动态规划
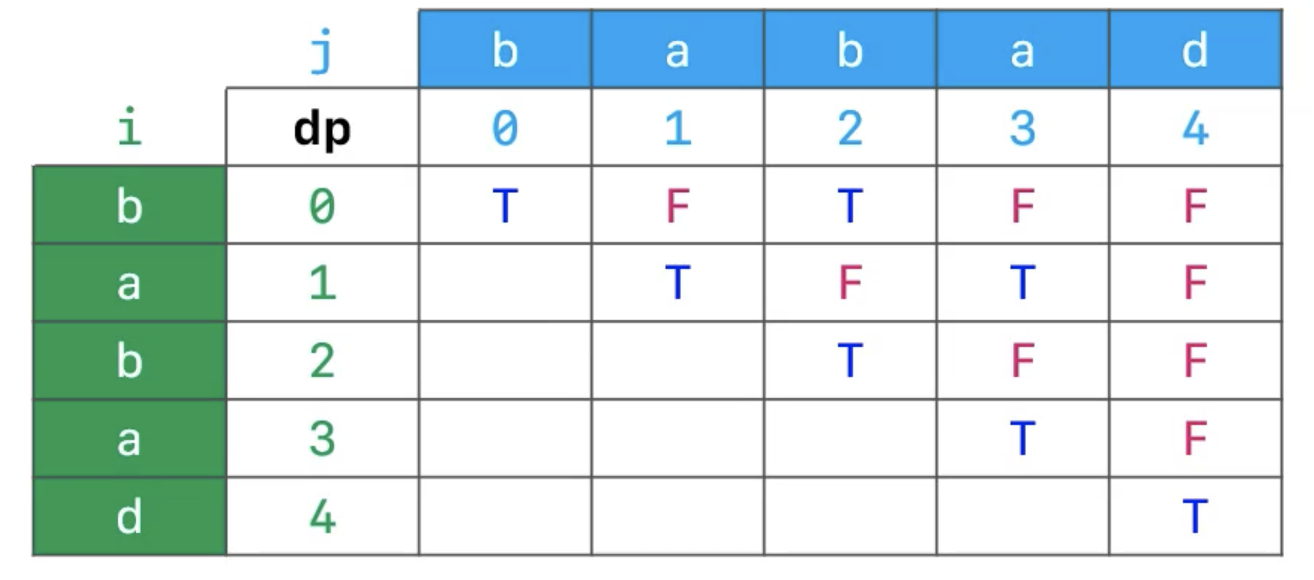
- 假设字符串
babad为s,长度为n- dp 是 大小为
n*n的二维数组,dp[i][j]表示s[i][j]是否为回文串,是存储 true,不是存储 false- 对角线元素表示,从某个字母到某个字母,也就是只有一个字母,所以必然是回文串
- 左下角为空,因为左下角部分表示倒着截取字符串,这不合理,只需要从左到右正着截取字符串就行了
- 综上应当满足
j ≥ i- 最终查看值为
true的格子,取j - i + 1的最大值
如何求
dp[i][j]的值
- 两种情况:
- 如果
s[i][j]的长度j - i + 1≤ 2:返回s[i]==s[j]:两个字符相等就是回文串
- 即:
dp[i][j]=s[i]==s[j]- 如果
s[i][j]的长度j - i + 1> 2:
- 如果
s[i + 1, j - 1]是回文串,且s[i]等于s[j],那么s[i, j]是回文串(去掉 i, j 指向的字符,看中间夹住的一段是不是回文串,如果是,就看 i, j 是不是相同的字符,如果是,那么s[i, j]就是回文串了)- 即:
dp[i][j]=dp[i + 1][j - 1]&& (s[i]==s[j])如何得到最长回文子串长度
- 每当某个
dp[i][j]的值为true就去看其对应的子串s[i, j]的长度- 记录最大长度
注意
实现时,应当从下往上,从左往右计算每个格子
public static String longestPalindrome(String s) {
if (s.length() == 1) return s;
char[] chars = s.toCharArray();
boolean[][] dp = new boolean[chars.length][chars.length];
int maxSubStrLen = 0; // 最大回文子串的长度
int maxSubStrI = 0; // 最大回文子串第一个字符的下标
for (int i = chars.length - 1; i >= 0; i--) {
for (int j = i; j < chars.length; j++) {
int currentSubStrLen = j - i + 1;
dp[i][j] = currentSubStrLen <= 2 ? chars[i] == chars[j] : (dp[i + 1][j - 1] && (chars[i] == chars[j]));
// 更新最大子串长度
if (dp[i][j] && (currentSubStrLen > maxSubStrLen)) {
maxSubStrLen = currentSubStrLen;
maxSubStrI = i;
}
}
}
return s.substring(maxSubStrI, maxSubStrI + maxSubStrLen);
}
- 时间复杂度 O(n ^ 2)
- 空间复杂度 O(n ^ 2)
扩展中心法
用 i 遍历数组
- 对每一个字符,同时向两边扩展探测,看字符是不是相等
- 相等:继续扩展一步,持续进行
- 不相等:记录当前长度,i++
- 遍历后,获知以每个字符为中心的最大回文子串长度
- 从中挑选出最大值
问题
这么搞,出来的回文子串长度永远是奇数
- 还要考虑偶数的情况
- 以字符间隙为中心,向左右扩散
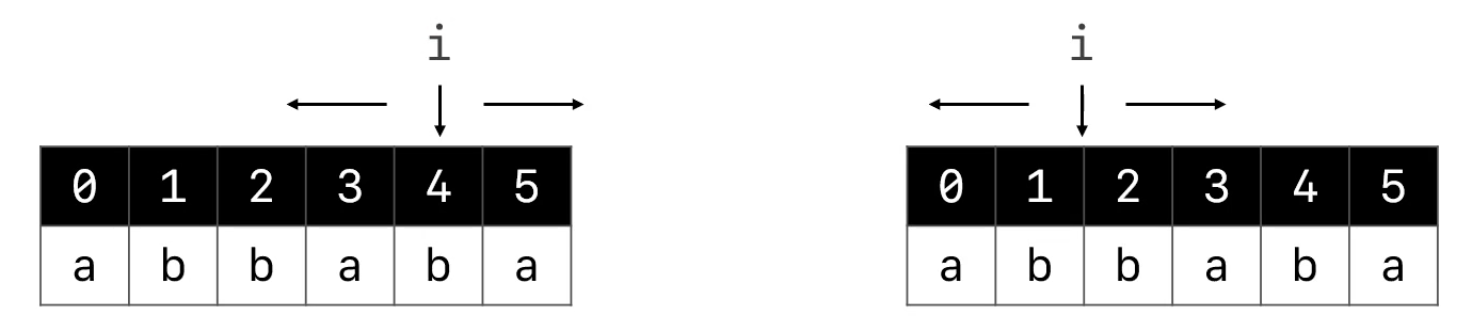
假设字符串
abbaba的长度为n, 那么一共有n + (n - 1)==2n - 1个扩展中心
- 从右向左扫描字符数组
- 开头的第一个字符必定只能跟自己形成回文串 (因为间隙概念的存在,所以不考虑它和左侧字符相同的情况)
- 结尾的最后一个字符同理,因此扫描范围为
[1, len - 2],但是会漏掉左侧开始数的第一个间隙- 用
i扫描字符数组,对于每一个i, 考虑 以当前指向的字符为中心 和 以当前指向字符右侧间隙为中心 的情况
- 分别确定
左、右两侧开始扩展扫描的索引下标
- 对于字符:左:
i-1;右:i+1- 对于间隙:左:
i;右:i+1- 分别计算出从字符开始和从间隙开始扩展,最终的最大回文子串长度,二者取最大值
- 二者的最大值 在和 总体最大值 比较,决定是否更新 总体最大值
- 如果要更新全局最大值,还要计算这种情况下,区间的左侧起始下标
- 左侧其实下标 = 中心下标 - (当前回文区间长度 - 1) / 2
- leftIndex = i - ((len - 1) / 2)
- 处理左侧第一个间隙
- s[0] 、 s[1] 是否相等
- 相等:是回文串,长度为 2 ,左侧下标为0
- 如果当前全局最大长度 < 2,那么就要更新,否则不管
- 不相等:不是回文串,不管
public class _5最长回文子串 {
public static String longestPalindrome(String s) {
if (s.length() == 1) return s;
char[] chars = s.toCharArray();
boolean[][] dp = new boolean[chars.length][chars.length];
int maxSubStrLen = 0; // 最大回文子串的长度
int maxSubStrI = 0; // 最大回文子串第一个字符的下标
for (int i = chars.length - 1; i >= 0; i--) {
for (int j = i; j < chars.length; j++) {
int currentSubStrLen = j - i + 1;
dp[i][j] = currentSubStrLen <= 2 ? chars[i] == chars[j] : (dp[i + 1][j - 1] && (chars[i] == chars[j]));
// 更新最大子串长度
if (dp[i][j] && (currentSubStrLen > maxSubStrLen)) {
maxSubStrLen = currentSubStrLen;
maxSubStrI = i;
}
}
}
return s.substring(maxSubStrI, maxSubStrI + maxSubStrLen);
}
// 扩展中心法
public static String longestPalindromeByCenterGrowth(String s) {
if (s.length() == 1) return s;
char[] chars = s.toCharArray();
int maxSubStrLen = 1;
int maxSubStrI = 0;
for (int i = chars.length - 2; i >= 1; i--) {
// 扫描所有的 字符 和 间隙
// 分别根据从当前字符扩展,还是从当前字符右侧的间隙扫描
// 从字符开始扩展获得的最大回文子串长度
int fromCharLen = palindromeLength(chars, i - 1, i + 1);
// 从字符右侧间隙开始扩展获得的最大子串长度
int fromSpaceLen = palindromeLength(chars, i, i + 1);
// 二者取较大的
fromCharLen = Math.max(fromCharLen, fromSpaceLen);
// 二者较大 再 与全局最大比较
if (fromCharLen > maxSubStrLen) {
maxSubStrLen = fromCharLen;
maxSubStrI = i - ((fromCharLen - 1) >> 1); // 左侧其实下标 = 中心下标 - (当前回文区间长度 - 1) / 2
}
}
// 处理 0 号字符右侧的间隙,第一个间隙
if (chars[0] == chars[1] && maxSubStrLen < 2) {
maxSubStrLen = 2;
maxSubStrI = 0;
}
return new String(chars, maxSubStrI, maxSubStrLen);
}
/**
* 从l向左;从r向右扫描;返回最长回文子串的长度
*
* @param chars 字符数组
* @param l 左侧扩展下标
* @param r 右侧扩展下标
* @return 从l向左;从r向右扫描;返回最长回文子串的长度
*/
private static int palindromeLength(char[] chars, int l, int r) {
while (l >= 0 && r < chars.length && chars[l] == chars[r]) { // 只要扩展出来的两个新字符相等
// 继续扩展
l--;
r++;
}
return r - l - 1;
}
public static void main(String[] args) {
String s = "bb";
String s1 = longestPalindromeByCenterGrowth(s);
System.out.println("s1 = " + s1);
}
}
- 时间复杂度 O(n ^ 2)
- 空间复杂度 O(1)
bai P3 1:06 优化