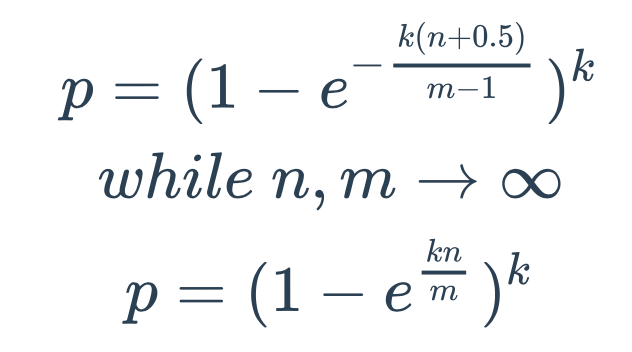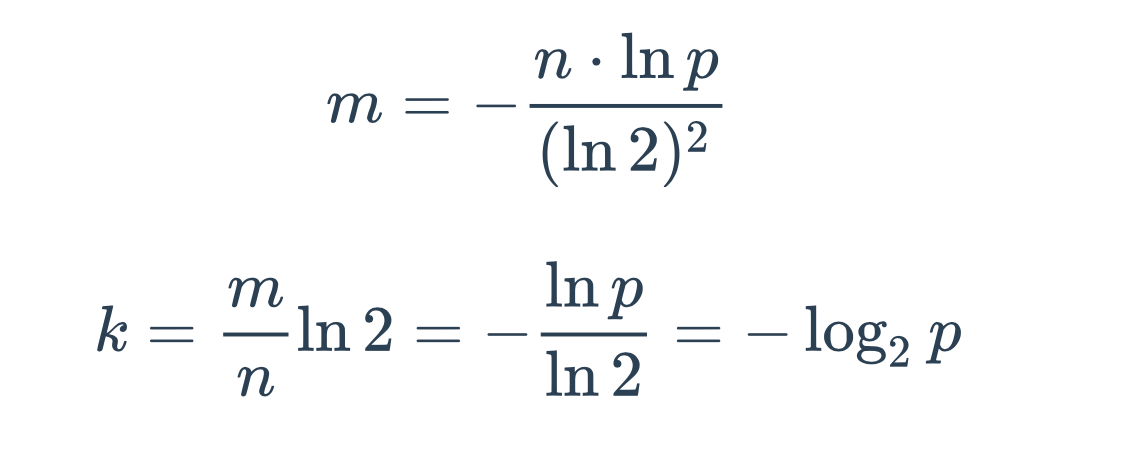布隆过滤器

思考

如果需要经常判断一个元素是否存在，应当怎么做？

• 容易想到使用哈希表（HashSet、HashMap），将元素作为 key 去查找
  • 时间复杂度 O(1)，但是空间利用率不高，需要占用比较多的内存资源
  • 如果需要判断的数据规模非常大，那么哈希表的空间规模会变得更大更大，非常夸张的大
• 是否存在时间复杂度低、且占用内存较少的方案？
  • 布隆过滤器——Bloom Filter

布隆过滤器

• 1970年由 布隆 提出
• 是一种 空间效率高 的 概率型 数据结构，可以用来反映：一个元素一定不存在 或 可能存在
  • 类比HashMap的 contains 方法，如果布隆过滤器有类似的方法，那么其返回 false 可以准确说明目标元素不存在，但如果返回 true 只能说明目标元素 可能存在
• 优缺点
  • 优点：空间效率和查询效率都远远超过一般数据结构
  • 缺点：有一定误判率、删除困难
• 适用场景（典型：Redis）
  • 经常需要判断某个元素是否存在
  • 元素数目非常巨大，希望适用尽可能少的内存空间
  • 允许存在一定误判率
• 本质：一个很长的二进制向量和一系列随机映射函数（Hash函数）
• 常见应用：
  • 网页黑名单系统
  • 垃圾邮件过滤系统
  • 爬虫网址判重系统
  • 解决缓存穿透问题

Guava 提供了基于 Java 的布隆过滤器实现

布隆过滤器原理

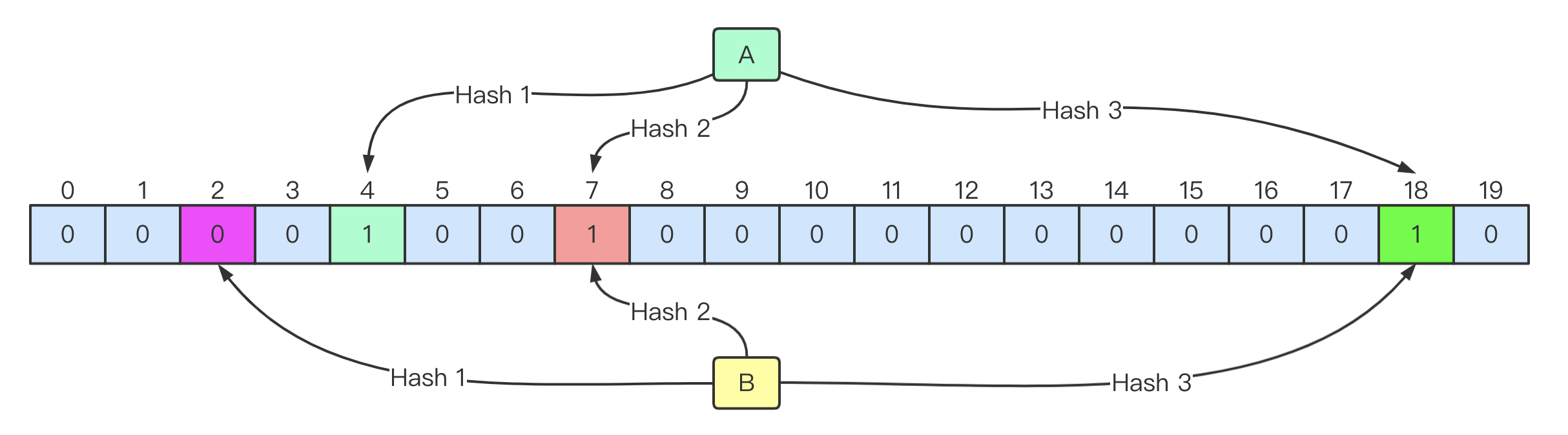
• 假设布隆过滤器由 20 二进制、3 个哈希函数组成，每个元素经过哈希函数处理都能生成一个索引位置

  

• 添加元素：将每一个哈希函数生成的 索引位置 都设置为 1

  

• 查询元素：借助哈希函数实现，查看每一个哈希函数计算出的索引

  • 只要有一个哈希函数生成的索引位置值不为 1，就表示目标元素 不存在，该结论 绝对准确
  • 每一个哈希函数生成的索引位置值都为 1，就表示目标元素 存在，该结论 存在误判率
    • 存在这种误判的原因是因为，不知道索引位置上的 1 是由哪个元素生成来的
    • 本质上还是哈希冲突问题

• 删除元素：很难删除
  • 将对应哈希计算出的索引对应位置的值设置为 0
  • 但是这些位置可不是专供某一个元素用的，可能是存在哈希冲突的，即 删除一个元素会影响别的元素
  • 可以对每一个位设置引用计数的概念，但是这样就麻烦了，违背了使用布隆过滤器的初衷，因此一般不提供删除方法

复杂度分析

设 k 是哈希函数的个数，m 是二进制向量的位数

操作	时间复杂度	空间复杂度
添加	O(k)	O(m)
查询	O(k)	O(m)

误判率控制

如何降低误判率

• 增加该向量的长度
• 设置更多的哈希函数

显然，在实际使用时，需要进行一定的权衡

理论公式

• 误判率 p 受 3 个因素的影响：二进制位数 m、哈希函数个数 k、数据规模 n

理论公式的实际应用

• 已知误判率 p、数据规模 n ，求二进制位的个数 m、哈希函数的个数 k

布隆过滤器的实现

API	功能
boolean put(T value)	插入元素
boolean contains(T value)	返回目标元素是否存在 false 绝对不存在 true 可能存在

成员变量

变量	含义
int bitSize	二进制向量的长度、一共有多少个二进制位
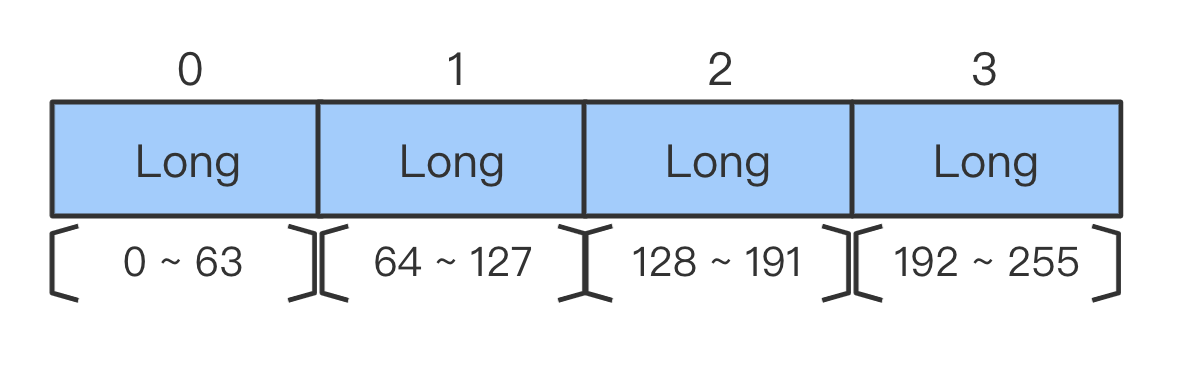
long[] bits	二进制向量本体，一个long为 8 个字节 64 bit 数组长度为 bitSize 除 64 向上取整 使用公式 (总数 + 页大小-1) / 页大小
int hashFunctionSize	哈希函数数目

构造方法

根据理论公式，要求传入期望的误判率 p、数据的规模 n

• 边际检查：排除数据规模小于等于0、误判率不在 (0, 1) 区间
• 自己计算出 需要的二进制位数 m、哈希函数的个数 k
• 计算出在上述 m 位的情况下，需要一个多大的 long[] 数组来表示二进制向量实体

成员变量与构造方法

// 二进制向量的长度，一共有多少个二进制位

private int bitSize;

// 二进制向量本体

private long[] bits;

// Hash函数数目

private int hashFunctionSize;

/**

* 构造方法，根据 数据规模、目标误判率、计算出需要的二进制位数和哈希函数数目

*

* @param n 数据规模 大于0

* @param p 目标误判率 属于 (0, 1)区间

*/

public MyBloomFilter(int n, double p) {

if (n <= 0 || p <= 0 || p >= 1)

throw new IllegalArgumentException("传入 数据规模 或 误判率 不合法");

// 计算 二进制向量长度 m、哈希函数数目 k

double ln2 = Math.log(2); // 计算 ln2

bitSize = (int) (-(n * Math.log(p)) / Math.pow(ln2, 2));

hashFunctionSize = (int) ((bitSize * ln2) / n);

// 计算二进制向量实体、本质是一个long数组，的数组长度

bits = new long[(bitSize + Long.SIZE - 1) / Long.SIZE];

}

插入方法

• 调用所有的哈希函数（参考 Guava 的哈希实现）
  obj.hashCode() -> hash处理1 -> 索引1
obj.hashCode() -> hash处理2 -> 索引2

• 模 上二进制向量的 长度 就可以得到 索引

• 将 索引 位置的二进制值设置为 1，使用 按位或 操作实现

  • 通过 索引 / Long.SIZE 得到目标二进制位在 第几个long
  
  • 在这个 long 内部，从右向左找到对应的二进制位
    • 计算内部偏移 offset = 索引 % Long.SIZE
    • 1 左移 (Long.SIZE - 1) - offset 即可得到对应二进制位的 One-Hot 掩码
    • 将该掩码与目标 long 进行 按位或 运算，即可将目标二进制位置 1
  • 将这个更新后的 long，存回 long[] 数组，覆盖旧的 long

查询方法

与插入方法类似，首先获得调用所有哈希函数，获得 索引、算出是哪个 long ，得到 内部偏移、将 1 左移 (Long.SIZE - 1) - offset

• 进行 按位与
  • 如果目标位为 0 ，计算结果必为 0
  • 如果目标位为 1， 计算结果必为 2的次幂
• 故，判断计算结果是否为 0
  • 结果为 0，返回目标位值为 0
  • 结果不为 0，返回目标位值为 1
• 如果目标二进制位的值为 0（任意一个哈希函数对应的索引），则可断言当前布隆过滤器不包含该元素
• 如果所有哈希函数对应的目标二进制位都不为 0，则当前布隆过滤器 可能包含目标元素

将目标二进制位设置为 1 的方法

/**

* 将 Index 位置的二进制位设置为 1

*

* @param index 索引

*/

private void set(int index) {

long targetLong = bits[index / Long.SIZE]; // 找到目标二进制位所在的那个 Long

int offset = index % Long.SIZE; // 目标 long 内部索引

targetLong |= 1 << ((Long.SIZE - 1) - offset);

bits[index / Long.SIZE] = targetLong; // 覆盖原来的 long

}

获取目标二进制位具体值的方法

/**

* 查询 index 位置的二进制值

*

* @param index 索引

* @return 索引位置上的二进制值

*/

private int get(int index) {

long targetLong = bits[index / Long.SIZE]; // 找到目标二进制位所在的那个 Long

int offset = index % Long.SIZE; // 目标 long 内部索引

return (targetLong & (1 << ((Long.SIZE - 1) - offset))) == 0 ? 0 : 1;

}

插入方法

public void put(T value) {

// 调用所有哈希函数

// 利用value 生成两个整数

int hash1 = value.hashCode();

int hash2 = hash1 >>> 16; // 无符号右移

for (int i = 1; i < hashFunctionSize; i++) {

int combinedHash = hash1 + (i * hash2); // 左hash处理

if (combinedHash < 0) // 如果计算出的联合哈希为负数，就取反

combinedHash = ~combinedHash;

// 取模，得到索引

int index = combinedHash % bitSize;

// 将索引位置的二进制位为 1

set(index);

}

}

查询方法

public boolean contains(T value) {

// 调用所有哈希函数

// 利用value 生成两个整数

int hash1 = value.hashCode();

int hash2 = hash1 >>> 16; // 无符号右移

for (int i = 1; i < hashFunctionSize; i++) {

int combinedHash = hash1 + (i * hash2); // 左hash处理

if (combinedHash < 0) // 如果计算出的联合哈希为负数，就取反

combinedHash = ~combinedHash;

// 取模，得到索引

int index = combinedHash % bitSize;

// 查询目标索引位置的二进制值是否为0

// 只要有一个为0，则绝对不包含当前所查询的 value元素

if (get(index) == 0) return false; // 必然不包含

}

return true; // 可能包含

}

测试

基本使用测试

• 插入若干个数，然后查询其是否存在于布隆过滤器中——期待返回 true
• 查询一个不曾插入的数，查询其是否在布隆过滤器中——期待返回 false

测试

public static void main(String[] args) {

MyBloomFilter<Integer> bloomFilter = new MyBloomFilter<>(100_0000, 0.01);

for (int i = 0; i < 10; i++)

bloomFilter.put(i);

for (int i = 0; i < 10; i++)

System.out.println("bloomFilter.contains(" + i + ") = " + bloomFilter.contains(i));

System.out.println("bloomFilter.contains(520) = " + bloomFilter.contains(520));

}

运行结果

bloomFilter.contains(0) = true

bloomFilter.contains(1) = true

bloomFilter.contains(2) = true

bloomFilter.contains(3) = true

bloomFilter.contains(4) = true

bloomFilter.contains(5) = true

bloomFilter.contains(6) = true

bloomFilter.contains(7) = true

bloomFilter.contains(8) = true

bloomFilter.contains(9) = true

bloomFilter.contains(520) = false

误判率测试

1. 插入 0 ~ 1000万 共 1000 万 个元素
2. 查询 1000万 ~ 9000万 是否存在于布隆过滤器中
   • 理想情况下应当全部不存在
   • 设定误判率为 0.01
   • 统计误判个数，计算实际误判率

误判率测试

public static void main(String[] args) {

MyBloomFilter<Integer> bloomFilter = new MyBloomFilter<>(8000_0000, 0.01);

// 先查 1000 万 个数据

for (int i = 0; i < 1000_0000; i++)

bloomFilter.put(i);

// 从 1000万 查看到 9000万

int errorCount = 0;

for (int i = 1000_0000; i < 9000_0000; i++)

if (bloomFilter.contains(i)) errorCount++; // 计算误判数

double errorP = errorCount / 8000_0000.0; // 计算误判率

System.out.printf("8千万个 [不存在] 的数，误判为 [存在] 共 [ %d ] 次，" +

"误判率为 [ %.7f ]", errorCount, errorP);

}

运行结果

8 千万个 [不存在] 的数，误判为 [存在] 共 [ 8 ] 次，误判率为 [ 0.0000001 ]