Version: Next
动态规划
Dynamic Programming,简称DP
- 是求解
最优化问题的一种常用策略
通常使用
套路,之后一步步进行优化(初学者)
- 暴力递归:自顶向下,出现重叠子问题
- 记忆化搜索(自顶向下)
- 递推(自底向上)
提示
动态规划有很多吓人的概念,对于初学者没啥好处,徒增心理压力,可以先忽略它们,以后再说
题目
- 1143.最长公共子序列
- 53.最大子序和
- 322.零钱兑换
- 300.最长上升子序列
- 70.爬楼梯
- 198.打家劫舍
- 213.打家劫舍2
- 674.最长连续递增序列
零钱问题
LeetCode 322
- 假设有
25、20、5、1块钱的硬币,现要给客户找41块钱,如何使使用的硬币最少
问题
之前使用 贪心算法 求解过,但一些情况下解答错误,因为 局部最优解 不一定就是 全局最优解
使用动态规划法求解(先忽略概念)
暴力递归阶段
- 假设
dp(n)是凑到n块钱所需要的最少硬币个数
- 例如:
dp(41)就表示凑到41块钱所需要的最少硬币个数- 思考取
第一枚硬币会出现的情况,一共有4种硬币可选
- 如果第一次选了
25块的硬币:已经选择了1枚25块钱的硬币,还需要凑到n - 25块钱需要的最少硬币数目个硬币,则dp(n) = dp(n - 25) + 1- 如果第一次选了
20块的硬币:同理,则dp(n) = dp(n - 20) + 1- 如果第一次选了
5块的硬币:同理,则dp(n) = dp(n - 5) + 1- 如果第一次选了
1块的硬币:同理,则dp(n) = dp(n - 1) + 1- 由于要求
最少硬币数,所以所求dp(n)就等于min{dp(n - 25), dp(n - 20), dp(n - 5), dp(n - 1)} + 1
与贪心算法的区别
- 上述过程实际上
考虑了所有情况,故可以找到全局最优解 - 贪心算法只
考虑眼前最优状况, 故只能找到局部最优解
代码实现(暴力递归阶段)
- 根据上述分析,使用
Math.min求出dp(n - 25), dp(n - 20), dp(n - 5), dp(n - 1)的最小值,再加上1- 思考递归调用的退出条件,从边界情况入手
- 如果
n = 25:选1枚25块钱的硬币,完毕,所以返回1,同理n = 20、5、1一样- 如果
n < 25:则dp(n - 25)传入了负数,显然负数是拿钱凑不出来的,这种情况下不能返回0,因为我们在找最小值,返回0,0很可能会成为较小的那个,因此返回整型最大值,针对n为负数的情况,进行递归退出处理
动态规划解零钱兑换问题(暴力递归阶段)
public class _322零钱兑换 {
/**
* 动态规划解零钱兑换问题,返回凑到 n 块钱所需要的最少硬币数目(暴力递归阶段)
*
* @param n 要换 n 块钱
* @return 使用的硬币个数
*/
public int coins(int n) {
// n > 25 等情况,出现传入参数为负数,进行递归退出处理
if (n < 1) return Integer.MAX_VALUE;
// 如果 n 正好等于面值,那么就选择一枚对应面值的硬币,返回 1
if (n == 25 || n == 20 || n == 5 || n == 1) return 1;
// 求出 dp(n-25),dp(n-20),dp(n-5),dp(n-1)的最小值
int min1 = Math.min(coins(n - 25), coins(n - 20));
int min2 = Math.min(min1, coins(n - 5));
int min = Math.min(min2, coins(n - 1));
return min + 1;
}
public static void main(String[] args) {
int n = 41;
int coins = new _322零钱兑换().coins(n);
System.out.println("想找 [" + n + "] 块钱零钱,最少需要 [" + coins + "] 块硬币");
}
}
运行结果
想找 [41] 块钱零钱,最少需要 [3] 块硬币
代码优化(记忆化搜索)
问题:从上述代码的形式上就能感觉到重复部分
- 例如调用了
coins(4),根据上述代码,会递归调用coins(3)、coins(2)、coins(1)
记忆化搜索
为了处理
重叠子问题,将部分已经计算过的内容,存储起来定义一个
数组 dp[],假设coins(16) = 4,则存储dp[16] = 4,为此数组的大小应当设置为n + 1对于给定的
4种面额,从小到大遍历,如果n大于目前的面额,则将数组对应位置的值设为1,直到面额比n大,或者遍历完了所有面额for (face : faces) {if (n < face) break;dp[face] = 1;}首先查看数组里有没有以前算好的值,没有算好的值就按之前的算法计算值,然后存到数组对应位置,有算好的就直接返回先前算好的值
思考递归退出条件:
n < 1:负数不能凑,数组也没有这样的下标,依然返回最大值
优化——记忆化搜索
/**
* 动态规划解零钱兑换问题,返回凑到 n 块钱所需要的最少硬币数目(记忆化搜索)
*
* @param n 要换 n 块钱
* @return 使用的硬币个数
*/
public int coins2(int n) {
if (n < 1) return -1;
// 记忆化数组
int[] dp = new int[n + 1];
int[] faces = {1, 5, 20, 25};
for (int face : faces) {
if (n < face) break;
dp[face] = 1;
}
return coins2(n, dp);
}
/**
* 动态规划解零钱兑换问题,返回凑到 n 块钱所需要的最少硬币数目(记忆化搜索)
*
* @param n 要换 n 块钱
* @param dp 记忆化数组
* @return 使用的硬币个数
*/
public int coins2(int n, int[] dp) {
if (n < 1) return Integer.MAX_VALUE;
// 查看记忆化数组
if (dp[n] == 0) { // 说明对应值没有计算过
int min1 = Math.min(coins2(n - 25, dp), coins2(n - 20, dp));
int min2 = Math.min(coins2(n - 5, dp), coins2(n - 1, dp));
// 将 min{..} + 1存到数组的对应位置上
dp[n] = Math.min(min1, min2) + 1;
}
// 否则直接取计算好的值
return dp[n];
}
public static void main(String[] args) {
int n = 41;
// int coins = new _322零钱兑换().coins(n);
int coins = new _322零钱兑换().coins2(n);
System.out.println("想找 [" + n + "] 块钱零钱,最少需要 [" + coins + "] 块硬币");
}
代码优化(自底向上——递推)
也称
迭代、非递归
- 之前的方法是
自顶向下的,例如求dp(6),会被分解为求dp(5)和dp(1)- 所以理论上可以倒过来,先求小的,再求大的,从
1遍历到n,求出每一个dp[i],其中dp[i] = dp[i - 25],dp[i - 20],dp[i - 5],dp[i - 1]的最小值再加1,而根据这个表达式,显然求dp[i]结果取决于比i小的dp值,所以理论上可以实现
自底向上递推
/**
* 动态规划解零钱兑换问题,返回凑到 n 块钱所需要的最少硬币数目(自底向上递推)
*
* @param n 要换 n 块钱
* @return 使用的硬币个数
*/
public int coins3(int n) {
if (n < 1) return -1;
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = Integer.MAX_VALUE;
if (i >= 1) min = Math.min(dp[i - 1], min);
if (i >= 5) min = Math.min(dp[i - 5], min);
if (i >= 20) min = Math.min(dp[i - 20], min);
if (i >= 25) min = Math.min(dp[i - 25], min);
dp[i] = min + 1;
}
return dp[n];
}
对于 n 恰好等于面额的情况,根据代码运行,会出现
dp[0]与Integer.MAX_VALUE之间比较,最终min = 0,dp[i] = 0 + 1 = 1,符合预期复杂度
O(n)
代码优化(打印零钱方案)
先前的代码只是打印了需要的硬币数目,如何把具体选了哪些硬币以及对应的面值打印出来
min是dp[i - 25]、dp[i - 20]、dp[i - 5]、dp[i - 1]的最小值,只需要直到是哪一个即可,如果min是dp[i - 25]就说明选了一枚25面额的,以此类推- 定义一个
数组faces[],长度为n + 1记录输入为i时所选择硬币的面额- 根据要凑的值
n,倒着查看最后一次选取的面额是多少,查看完之后,n - 最后一次面额,就是还要凑的值,继续到faces数组中去查,形成一个循环,不断的减最后一次面额,直到全部凑完- 最后要将这些面额逆序一下,因为是倒着查的,最终就是按顺序每次选择的面额
显示具体的选择
/**
* 动态规划解零钱兑换问题,返回凑到 n 块钱所需要的最少硬币数目(自底向上递推)
* 带有方案打印功能
*
* @param n 要换 n 块钱
* @return 使用的硬币个数
*/
public int coinsWithShow(int n) {
if (n < 1) return -1;
int[] dp = new int[n + 1];
int[] faces = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = Integer.MAX_VALUE;
if (i >= 1) {
min = Math.min(dp[i - 1], min);
if (min == dp[i - 1]) faces[i] = 1;
}
if (i >= 5) {
min = Math.min(dp[i - 5], min);
if (min == dp[i - 5]) faces[i] = 5;
}
if (i >= 20) {
min = Math.min(dp[i - 20], min);
if (min == dp[i - 20]) faces[i] = 20;
}
if (i >= 25) {
min = Math.min(dp[i - 25], min);
if (min == dp[i - 25]) faces[i] = 25;
}
dp[i] = min + 1;
}
showPick(faces, n);
return dp[n];
}
/**
*
* @param faces 输入为i时,对应选择的面额
* @param n 要凑的总数
*/
private void showPick(int[] faces, int n){
Stack<Integer> resultSet = new Stack<>();
int remain = n; // 还要凑多少钱
int lastPickFace = 0; // 最后一次选择的面额
while (remain > 0) {
lastPickFace = faces[remain];
// 在这里处理结果集
// 将最后一次选择的面额存到结果集
resultSet.push(lastPickFace);
// 在这里处理结果集
remain = remain - lastPickFace;
}
// 利用栈逆序
while (resultSet.iterator().hasNext()) {
System.out.println("选取了面额为 [" + resultSet.pop() + "] 的硬币");
}
}
public static void main(String[] args) {
int n = 41;
int coins = new _322零钱兑换().coinsWithShow(n);
System.out.println("想找 [" + n + "] 块钱零钱,最少需要 [" + coins + "] 块硬币");
}
运行结果
选取了面额为 [1] 的硬币
选取了面额为 [20] 的硬币
选取了面额为 [20] 的硬币
想找 [41] 块钱零钱,最少需要 [3] 块硬币
代码优化(通用面额)
通用面额
/**
* 可以从外部接收面额数组的通用零钱问题方法
*
* @param n 要凑的钱
* @param faces 外部面额数组
* @return 选取硬币的个数
*/
public int coins(int n, int[] faces) {
if (n < 1 || faces == null || faces.length == 0) return -1;
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = Integer.MAX_VALUE;
for (int face : faces)
if (i >= face) min = Math.min(dp[i - face], min);
dp[i] = min + 1;
}
return dp[n];
}
测试
public static void main(String[] args) {
int n = 41;
int[] faces = {1, 5, 25, 25};
int coins = new _322零钱兑换().coins(n, faces);
System.out.println("想找 [" + n + "] 块钱零钱,最少需要 [" + coins + "] 块硬币");
}
运行结果
想找 [41] 块钱零钱,最少需要 [5] 块硬币
代码优化(凑不出的情况)
如果给出的面额永远凑不出目标数字,算法应当返回
-1
- 假设面值为
[5, 20, 25]
- 情况一:目标值比最小面额
5还小,比如说n = 3
- 直接在遍历面额阶段进行判断
- 情况二:目标值比最小面额
5大,但是依然凑不出来,比如n = 6
- 只有
i大于当前面值,且dp[i - 面值]大于等于0时(表示剩余值能凑出来),才进行选取
处理凑不出的情况
/**
* 可以从外部接收面额数组的通用零钱问题方法
*
* @param n 要凑的钱
* @param faces 外部面额数组
* @return 选取硬币的个数
*/
public int coins(int n, int[] faces) {
if (n < 1 || faces == null || faces.length == 0) return -1;
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
int min = Integer.MAX_VALUE;
for (int face : faces) // 剩余值能凑出才选取
if (i >= face && dp[i - face] >= 0) min = Math.min(dp[i - face], min);
// 跑完了所有面值,min的值没有发生变化,说明目标值比最小面额都小
// 将dp[i] 设置为 -1
if (min == Integer.MAX_VALUE) dp[i] = -1;
else dp[i] = min + 1;
}
return dp[n];
}
测试
public static void main(String[] args) {
int n1 = 3;
int n2 = 6;
int[] faces = {5, 20, 25};
int coins1 = new _322零钱兑换().coins(n1, faces);
int coins2 = new _322零钱兑换().coins(n2, faces);
System.out.println("想找 [" + n1 + "] 块钱零钱,最少需要 [" + coins1 + "] 块硬币");
System.out.println("想找 [" + n2 + "] 块钱零钱,最少需要 [" + coins2 + "] 块硬币");
}
运行结果
想找 [3] 块钱零钱,最少需要 [-1] 块硬币
想找 [6] 块钱零钱,最少需要 [-1] 块硬币
动态规划解释
动态规划中的
动态可以理解为是会变化的状态
步骤
- 定义状态——状态是原问题、子问题的解
- 例如
dp[i]的含义——要凑出i块钱需要的最少硬币数- 设置初始状态(边界情况)
- 例如
设置 dp[0] 的值,也可能是dp[1]等- 总之是需要特殊处理的边界情况
- 或者是可以立刻得到的子问题的解,例如零钱问题目标值为
1,面额为1则立刻得dp[1] = 1- 确定状态转移方程(递推)
- 例如 确定
dp[i]与dp[i - 1]的关系
动态规划相关概念
维基百科
Dynamic Programmingis a method for solving a complex problem by breaking it down into a collection ofsimpler subproblems, solving each of those subproblemsjust once, andstoringtheir solutions.动态规划是指一种通过将复杂问题分解为一堆简单子问题的集合来将其求解的方法,只需解决这些子问题1次,并且将这些子问题的解进行存储
- 将复杂原问题拆解为若干简单的子问题
- 每个子问题仅仅解决
1次,并把他们的解存起来- 最后推导出原问题的解
可以用动态规划解决的问题,通常具有
2个特点
- 最优子结构(最优化原理):通过求解子问题的最优解,可以获得原问题的最优解
- 无后效性
- 某阶段的状态一旦确定,则此后过程的演变不再受此前个状态及决策的影响(未来与过去无关)
- 在推导后续阶段的状态时,只关心前面阶段的具体状态值,不关心其状态是如何一步步推导出来的
无后效性详解
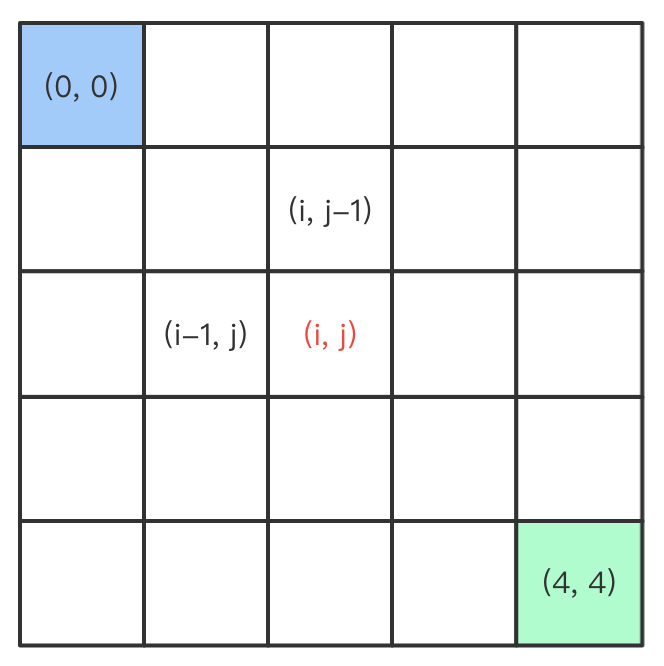
引例:从起点
(0, 0)走到终点(4, 4)一共有多少种走法?只能向右、向下移动
- 定义状态:假设
dp(i, j)是从(0, 0)走到(i, j)的走法- 边界状态:
dp(0, 0) = 1dp(i, 0) = dp(0, j)= 1第一列、第一行的格子都只有一种走法- 状态转移方程:
dp(i, j) = dp(i-1, j) + dp(i, j-1)
无后效性
- 推导
dp(i, j)时只需要用到dp(i-1, j)和dp(i, j-1)的值- 不关心
dp(i-1, j)和dp(i, j-1)是如何推导出来的
有后效性
同样的问题,现在可以向上、下、左、右移动,同一个格子不能走
2次
有后效性——不能用动态规划解决
- 通过
(i, j)推导之后的走法时,受到先前状态的影响
- 允许的走法很多,不确定先前是如何走的
- 又因为一个格子不能走
2次