Version: Next
53. 最大子序和
难度 简单
给定一个整数数组
nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]输出: 6解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
53. Maximum Subarray
难度 简单
Given an integer array
nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.Follow up: If you have figured out the
O(n)solution, try coding another solution using the divide and conquer approach, which is more subtle.Example 1:
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]Output: 6Explanation: [4,-1,2,1] has the largest sum = 6.Example 2:
Input: nums = [1]Output: 1Example 3:
Input: nums = [0]Output: 0Example 4:
Input: nums = [-1]Output: -1Example 5:
Input: nums = [-2147483647]Output: -2147483647Constraints:
1 <= nums.length <= 2 * 104-231 <= nums[i] <= 231 - 1
这道题也属于最大切片问题(最大区段,Greatest Slice)
- 概念区分
- 子串、子数组、子区间必须是连续的,子序列可以不连续
暴力法
- 穷举所有可能的连续子序列,分别计算出它们的和,最后取其中的最大值
暴力法
public class _53最大连续子序和 {
public static int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int sum = Integer.MIN_VALUE; // 这
for (int begin = 0; begin < nums.length; begin++) {
for (int end = begin; end < nums.length; end++) {
int currentSum = 0;
for (int i = begin; i <= end; i++) { // 区间求和
currentSum += nums[i];
}
if (currentSum > sum) sum = currentSum;
}
}
return sum;
}
public static void main(String[] args) {
int[] nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
int sum = maxSubArray(nums);
System.out.println("sum = " + sum);
}
}
运行结果
sum = 6
- 时间复杂度
O(n3)
分治法
- 将序列均匀地分割为
2个子序列[begin, end] = [begin, mid) + [mid, end],其中mid = (begin + end) / 2实现时用位运算实现- 假设有一个解决该问题的数学函数
S[i, j],它返回从i开始到j结束的连续子序列的和,则问题的解有3种可能
- 区间
[i, j]在切割出来的2个子序列的左子序列中- 区间
[i, j]在切割出来的2个子序列的右子序列中- 区间
[i, j]横跨了切割出来的2个子序列,被切分为[i, mid)和[mid, j]- 递归分割,递归退出条件:
- 切分到只剩
2个,返回这两个数及这两个输的和,三者的最大值- 切分到只剩
1个,返回这个唯一的数
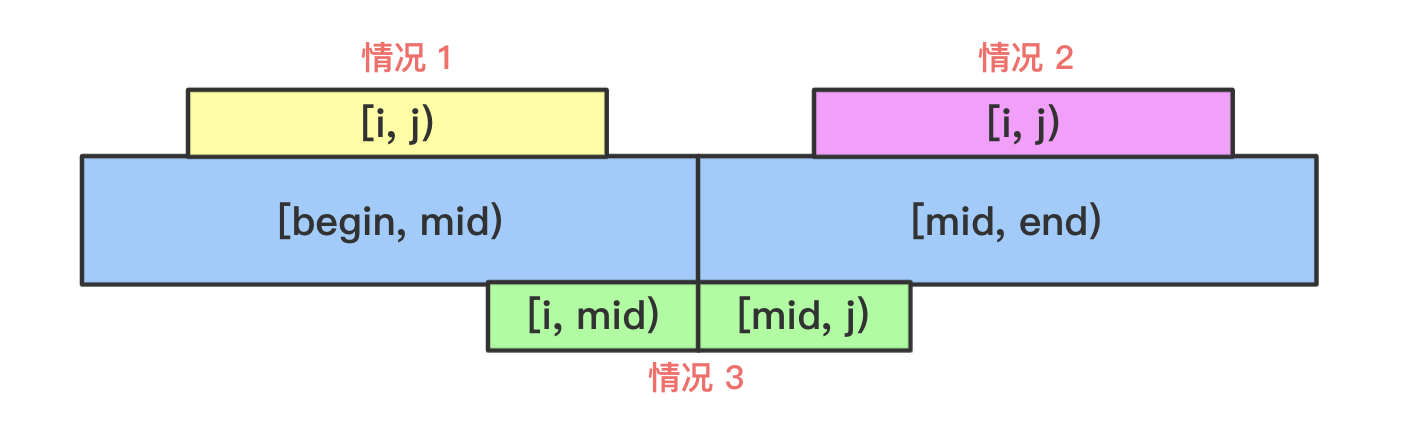
对于
情况 3,思考其具有的特点
[i, mid)是那一部分?:从mid出发,向左逐个元素求和,直到找出其最大和 ,之间的子序列就是[i, mid)- 同理, 从
mid触发,向右逐个元素求和,直到找出其最大和 ,之间的子序列就是[mid, j]
public class _53最大连续子序和 {
public static int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
return maxSubArray(nums, 0, nums.length - 1);
}
/**
* 求解 begin 到 end 之间,最大连续子序列的和
*
* @param nums 给定序列
* @param begin 起点指针
* @param end 终点指针
* @return 最大子序列和
*/
private static int maxSubArray(int[] nums, int begin, int end) {
if (end - begin == 1) // 只剩两个
return Math.max(nums[begin] + nums[end], Math.max(nums[end], nums[begin]));
if (end == begin) // 只剩一个
return nums[begin];
int mid = (begin + end) >> 1;
// 分割成 2 个
int leftMax = maxSubArray(nums, begin, mid); // 求左边最大子序列和
int rightMax = maxSubArray(nums, mid, end); // 求右边最大子序列和
// 处理情况 3
int leftMidMax = Integer.MIN_VALUE;
int rightMidMax = Integer.MIN_VALUE;
// 从mid开始,向左逐个求和,找出最大和
int currentSum = 0;
for (int i = mid - 1; i >= begin; i--) {
currentSum += nums[i];
leftMidMax = Math.max(leftMidMax, currentSum);
}
// 从mid开始,向右逐个求和,找出最大和
currentSum = 0;
for (int i = mid; i <= end; i++) {
currentSum += nums[i];
rightMidMax = Math.max(rightMidMax, currentSum);
}
int midMax = leftMidMax + rightMidMax;
return Math.max(midMax, Math.max(leftMax, rightMax));
}
public static void main(String[] args) {
int[] nums1 = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
int[] nums2 = {-1};
int[] nums3 = {-2, 1};
int[] nums4 = {1, 2};
int[] nums5 = {1};
int sum1 = maxSubArray(nums1);
int sum2 = maxSubArray(nums2);
int sum3 = maxSubArray(nums3);
int sum4 = maxSubArray(nums4);
int sum5 = maxSubArray(nums5);
System.out.println("sum1 = " + sum1); // expect 6
System.out.println("sum2 = " + sum2); // expect -1
System.out.println("sum3 = " + sum3); // expect 1
System.out.println("sum4 = " + sum4); // expect 3
System.out.println("sum5 = " + sum5); // expect 1
}
}
问题
这种写法比较符合我个人的思路
- 根据题解,如果严格将所有区间的表示形式规定为左闭右开,可以进一步简化递归退出条件
左闭右开区间
public static int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
return maxSubArray(nums, 0, nums.length); // 修改为左闭右开,所以不再 -1
}
/**
* 求解 begin 到 end 之间,最大连续子序列的和
*
* @param nums 给定序列
* @param begin 起点指针
* @param end 终点指针
* @return 最大子序列和
*/
private static int maxSubArray(int[] nums, int begin, int end) {
if (end - begin < 2) // 修改为左闭右开 进入此if 必定分割到只有1个元素
return nums[begin]; // 故直接返回
int mid = (begin + end) >> 1;
// 分割成 2 个
int leftMax = maxSubArray(nums, begin, mid); // 求左边最大子序列和
int rightMax = maxSubArray(nums, mid, end); // 求右边最大子序列和
// 处理情况 3
int leftMidMax = Integer.MIN_VALUE;
int rightMidMax = Integer.MIN_VALUE;
// 从mid开始,向左逐个求和,找出最大和
int currentSum = 0;
for (int i = mid - 1; i >= begin; i--) {
currentSum += nums[i];
leftMidMax = Math.max(leftMidMax, currentSum);
}
// 从mid开始,向右逐个求和,找出最大和
currentSum = 0;
for (int i = mid; i < end; i++) { // 修改为作弊又开,所以不能再加等号 =
currentSum += nums[i];
rightMidMax = Math.max(rightMidMax, currentSum);
}
int midMax = leftMidMax + rightMidMax;
return Math.max(midMax, Math.max(leftMax, rightMax));
}
复杂度分析
- 分治数据规模一分为二
- 对于情况3,从mid开始向两侧求和为
O(n) T(n) = T(n / 2) + T(n / 2) + O(n)- 根据分治法主定理,此处a = 2, b = 2, d = 1
- 则
log_b (a) = 1,又d = 1,则满足d = log_b (a)的情况 - 故根据主定理结论:
T(n) = O(n^d * logn) = O(nlogn)
动态规划
对于 [-2, 1, -3, 4, -1, 2, 1, -5, 4]
- 定义状态(难点)
- 假设
dp(i)是以第i个元素nums[i]结尾 的最大连续子序列和
- 以
nums[0] = -2结尾的最大连续子序列是[-2],所以dp(0) = -2- 以
nums[1] = 1结尾的连续子序列是[-2, 1]和[1],最大连续子序列为[1],所以dp(1) = 1- 以
nums[2] = -3结尾的最大连续子序列是[1, -3],所以dp(2) = dp(1) + (-3) = -2- 以
nums[3] = 4结尾的最大连续子序列是[4],所以dp(3) = 4- 以
nums[4] = -1结尾的最大连续子序列是[4, -1],所以dp(4) = dp(3) + (-1) = 3- 以
nums[5] = 2结尾的最大连续子序列是[4, -1, 2],所以dp(5) = dp(4) + 2 = 5- 以
nums[6] = 1结尾的最大连续子序列是[4, -1, 2, 1],所以dp(6) = dp(5) + 1 = 6- 以
nums[7] = -5结尾的最大连续子序列是[4, -1, 2, 1, -5],所以dp(7) = dp(6) + (-5) = 1- 以
nums[8] = 4结尾的最大连续子序列是[4, -1, 2, 1, -5, 4],所以dp(8) = dp(7) + 4 = 5- 初始、边界状态
dp(0)的值必然是nums[0]- 状态转移方程
- 在求
dp(i)的时候,应当参考dp(i - 1)的值,即前一个的值
- 如果前一个的值不是
正数,那就没必要加上它,因为会让连续子序列和变小- 否则,说明
dp(i - 1)是个正数,那就把它带上,再加上当前结尾值if (dp[i - 1] <= 0)dp[i] = nums[i];elsedp[i] = dp[i - 1] + nums[i];
- 所求解即为
dp(0)到dp(8)中的最大值
动态规划法
public static int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int[] dp = new int[nums.length];
// 初始状态,dp[0] 必然等于 nums[0]
dp[0] = nums[0];
int max = dp[0];
for (int i = 1; i < nums.length; i++) {
// 状态转移返程
if (dp[i - 1] <= 0)
dp[i] = nums[i];
else
dp[i] = dp[i - 1] + nums[i];
// 输出dp数组中的最大值
max = Math.max(max, dp[i]);
}
return max;
}
优化
- 注意:实际上求
dp[i],只需要参考dp[i - 1]就够了,再前面的值根本用不上- 所以实际上没必要弄个
dp数组,只需要前一个值就行了
移除dp数组
public static int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int current = 0;
int last = nums[0];
int max = last;
for (int i = 1; i < nums.length; i++) {
// 状态转移返程
if (last <= 0)
current = nums[i];
else
current = last + nums[i];
// 输出dp数组中的最大值
max = Math.max(max, current);
last = current;
}
return max;
}
复杂度分析
空间复杂度:O(1)
时间复杂度:O(n)