Version: Next

堆排序

对排序可以认为是对选择排序的优化

执行流程
对序列进行原地建堆（Heapify）
重复执行以下操作，直到堆的元素数量 size 为 1
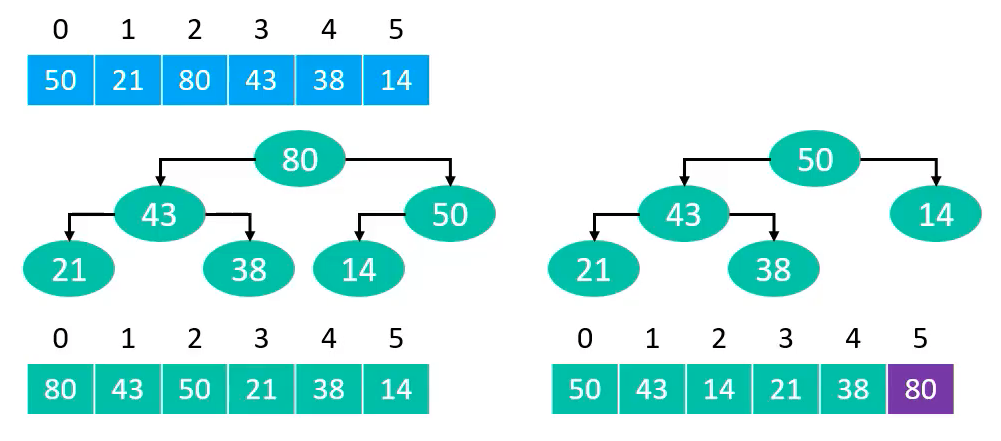
交换堆顶元素和尾元素（即交换当前堆中的最大值和最小值）
堆的元素数量 -1，size -= 1
对 0 位置进行 1 次 siftDown 操作，让它排列到堆中的合适位置

复杂度分析
生成 n 次堆，O(n)
对每一个堆
交换元素 O(1)
size - 1 ， O(1)
siftDown，需要进行二分搜索，O(logn)
最终 O(nlogn)

/**
 * 对排序
 */
public class HeapSort<E extends Comparable<E>> extends Sort<E> {
    private int heapSize;

    public HeapSort(E[] array) {
        this.array = array;
    }

    @Override
    public void sort() {
        // 原地建堆
        heapSize = array.length;
        for (int i = (heapSize >> 1) - 1; i >= 0; i--) {
            siftDown(i);
        }

        while (heapSize > 1) {
            swap(0, heapSize - 1); // 交换头尾
            heapSize--;
            // 对 0 位置进行 siftDown()
            siftDown(0); // 排列，位置堆的性质
        }
    }

    private void siftDown(int index) {
        E element = this.array[index];

        int half = heapSize >> 1;
        while (index < half) { // index 必须是非叶子节点
            // 默认是左边根父节点比
            int childIndex = (index << 1) + 1;
            E child = this.array[childIndex];

            int rightIndex = childIndex + 1;
            // 右子节点比左子节点大
            if (rightIndex < heapSize && cmp(this.array[rightIndex], child) > 0)
                child = this.array[childIndex = rightIndex];

            // 大于等于子节点
            if (cmp(element, child) >= 0) break;

            this.array[index] = child;
            index = childIndex;
        }

        this.array[index] = element;
    }

    public static void main(String[] args) {
        Integer[] array = {4, 5, 2, 3, 1};
        HeapSort<Integer> integerHeapSort = new HeapSort<>(array);
        integerHeapSort.sort();
        for (Integer integer : array) {
            System.out.println(integer + " ");
        }
    }
}

堆排序#

堆排序