计数排序

info

冒泡、选择、插入、归并、快速、希尔、堆排序都是基于 比较 的排序

• 平均时间复杂度最低为 O(nlogn)

计数排序、桶排序、基数排序，都不是基于比较的排序

• 典型的空间换时间，在某些场景下，平均时间复杂度可以比 O(nlogn) 更低

计数排序

• 1954 年由 Harold H. Seward 提出，适合对一定范围内的正数进行排序
• 核心思想：统计每个整数在序列中出现的次数，进而推导出每个整数在 有序序列 中的索引

最简实现

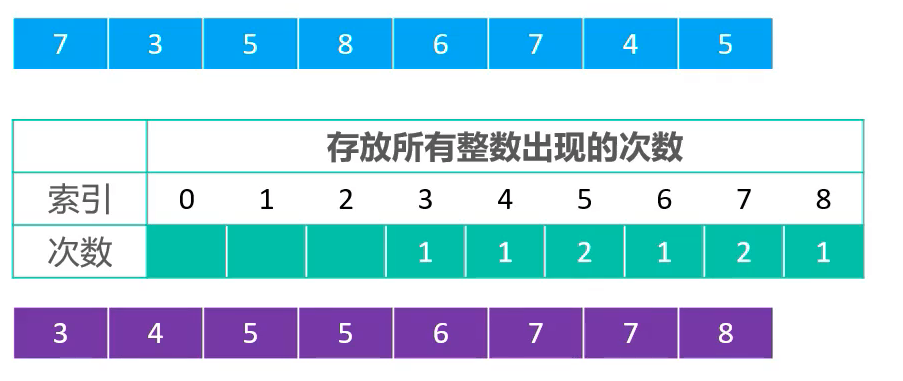
• 用一个数组存储元素出现的次数，数组长度为 元素最大值 + 1
  • 数字 1 出现的次数就记录在 数组 array[1] 位置
  • 数字 20 出现的次数就记录在 数组 array[20] 位置
• 从左向右扫描数组，只要元素有值就输出对应下标，值为几就输出几次

/**

* 计数排序 最简实现

*/

public class CountingSort1 extends Sort<Integer> {

public CountingSort1(Integer[] array) {

this.array = array;

}

@Override

public void sort() {

// 找出元素最大值

int max = array[0];

for (int i = 1; i < array.length; i++)

if (array[i] > max) max = array[i];

// 开辟内存空间，存储每个整数出现的次数

int[] countArray = new int[max + 1];

for (int i = 0; i < array.length; i++)

countArray[array[i]]++;

int current = 0; // 记录当前操作位置的指针

// 遍历表格输出

for (int i = 0; i < countArray.length; i++)

while (countArray[i]-- > 0)

// 直接覆盖 原数组array]

array[current++] = i;

/* current++;

countArray[i]--;*/

}

public static void main(String[] args) {

Integer[] array = {4, 5, 3, 2, 1, 1};

new CountingSort1(array).sort();

for (Integer integer : array) {

System.out.println(integer + " ");

}

}

}

问题

• 无法对负数进行排序
• 极其浪费内存空间
• 不稳定排序

改进

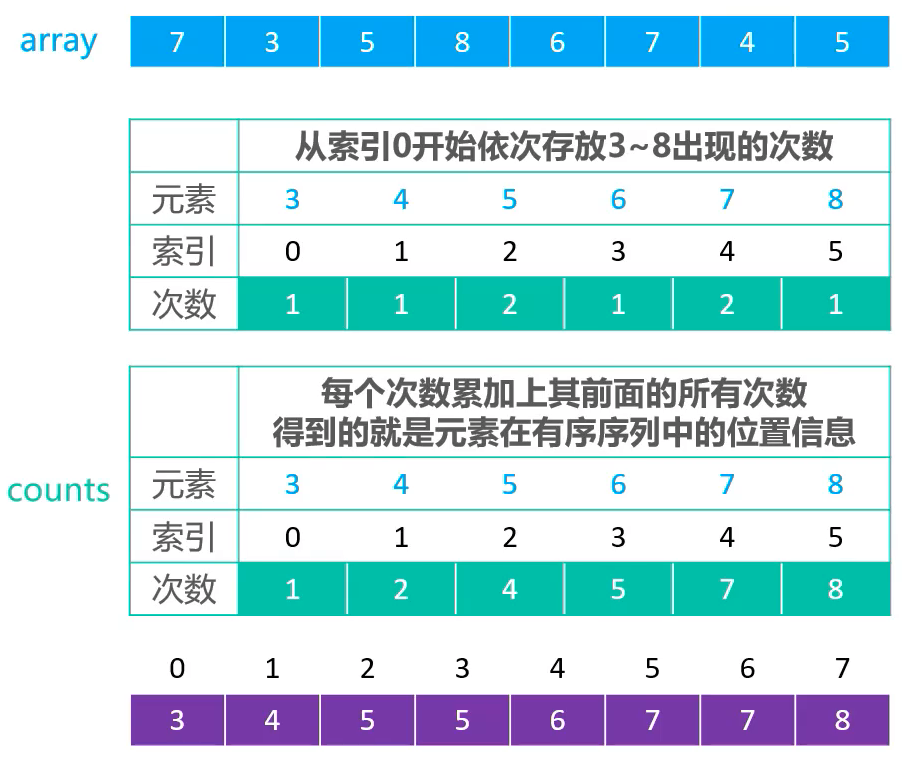
• 从索引 0 开始，依次存放元素出现的次数
• 每个次数累加上前面所有次数，得到的就是元素在有序序列中的位置信息
  • 从右向左遍历，当前元素的索引 = 当前元素值（累计次数） - 当前次数