Version: Next

八皇后问题

八皇后问题是一个古老而经典的问题

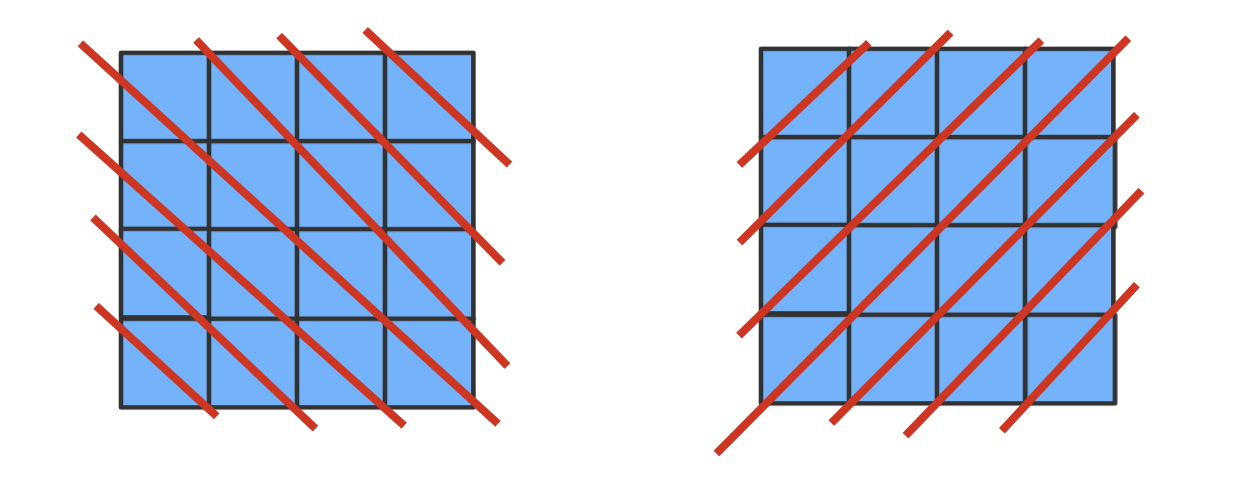
  • 在 8 x 8 的国际象棋盘上摆放8个皇后，使其不能相互共计，任意两个皇后都不能处于同一行、同一列和同一斜线上
  • 问：共有多少种摆法
Leetcode题目

51.N皇后Ⅰ

52.N皇后Ⅱ

解决思路

暴力法

在64个格子中，任意选出8个格子，检查每一种摆法的可行性

  • 根据排列组合，共有C 64 8 种组合，共4.4 * 10 ^ 9种，即44亿

回溯法

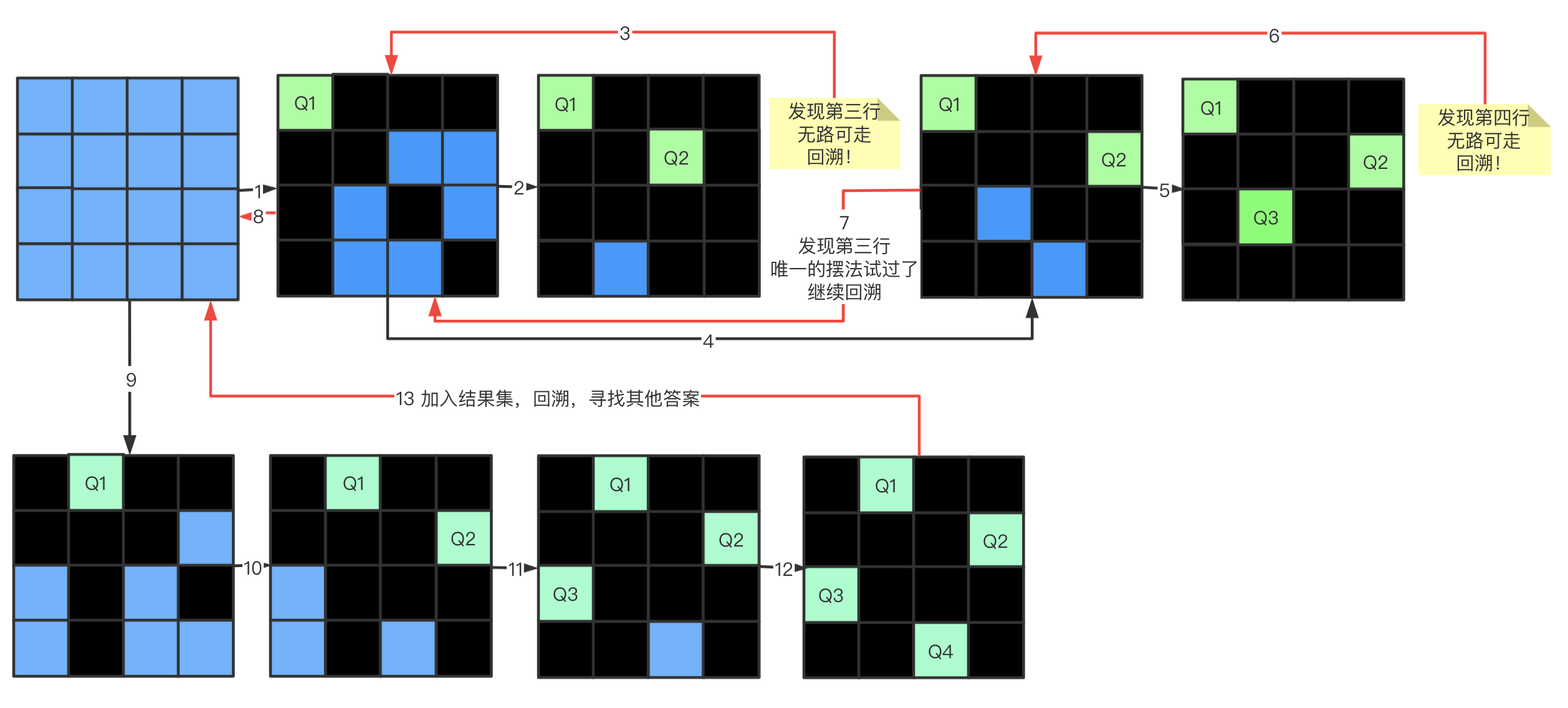
四皇后问题

在解决八皇后问题之前，可以先通过缩小数据规模的方式，看看如何解决四皇后问题

  • 蓝色：可摆放
  • 绿色：已摆放
  • 黑色：不能摆放
  • 红色箭头：回溯

image-20201208150804285

编程实现

  • 对于二叉树、图等数据结构，以节点为单位，类比到这里，对于八皇后问题，以行为单位

  • 定义一个数组cols，索引是行号，元素是列号，用来记录皇后摆放的位置

    • 例如cols[4] = 5表示，第五行的皇后在第六列

  • 定义一个检查规则的方法boolean isValid(int 行, int 列)，用于检查每个具体格子符不符合国际象棋规则，即检查它能不能被剪枝

    • 遍历之前所有行，查看每一行摆放皇后所在的列，如果正好等于当前列，则立刻返回false
    • 当前行是全新的一行，所以不用在行维度上检查
    • 检查斜线：有多种方法
      • 斜率法：行坐标 - 列坐标结果相等的，在同一直线（斜线）上，如果加上绝对值，那么也满足其垂线，整合起来就是在其所有斜线方向上，即cols[i] - i == col - row，等价的，进行移项得到cols[i] - col == i - row，再移项得到分式(cols[i] - col) / i - row == 1即直线方程的标准形式之一(y1 - y2) / (x1 - x2) = k，说明两点在同一直线（斜线）上

  • 从第1行开始摆放皇后，每一行都有最多八种摆法，写一个在某一行开始摆放皇后的方法place(int row)

    • 在每一行上，遍历所有列，检查哪个位置可以摆放皇后，按照国际象棋规则检查不能摆的位置，即进行剪枝操作

    • 剪枝的依据是，当前行之前的所有行的皇后摆法

      • 不符合规则：剪枝

      • 符合规则：立刻摆放皇后，然后跳到下一行，即place(row + 1)，出现递归

    • 如果程序执行到了place(row + 1)的下一行，说明没有执行row + 2那一行的摆放，即row + 1行没法摆了，所以函数跑完了遍历一行的for循环，而place(row + 1)的调用位置恰是place(row)的代码中，可视为自动进行了回溯

    • 如果开始摆放下标为8的行，说明全部的皇后都摆进去了，这就是place方法的递归退出条件，令结果集+1，然后退出递归

/**
* 八皇后问题 —— 回溯法
*/
public class EightQueens {
int[] cols; // 数组索引时行号，数组元素是列号，用来记录皇后摆放的位置
int numOfSolutions; // 可用摆法计数
// 摆放n个皇后的方法
public void placeQueens(int n) {
if (n < 1) return;
// 在 第0行 摆放第一个皇后
cols = new int[n]; // 初始化位置数组
place(0);
// 走到这里，说明所有递归调动结束了
System.out.println("当前为 [" + n + "] 皇后问题，共有 [" + numOfSolutions + "] 种摆法");
}
// 从第 row 行开始摆放1皇后
public void place(int row) {
// 递归退出条件，如果row == n，即8，说明所有的皇后已经摆好了
if (row == cols.length) {
// 结果集+1，退出递归
numOfSolutions++;
return;
}
// 遍历一行中的所有列
for (int col = 0; col < cols.length; col++) { // 从第0列到第8列
// 查看哪个位置能摆
if (isValid(row, col)) { // 合法、有效、可以摆放皇后
// 能摆，那就摆
cols[row] = col;
// 摆完，立刻摆下一行
place(row + 1);
// 能执行到这个位置，发生回溯，走下一列了
}
// 来到这里，表示非法，无效，不能摆放皇后，就剪枝，剪枝就啥也不干
}
}
// 检查国际象棋规则的方法，用于剪枝
// 传入行列，确定一个唯一的格子，返回这个格子需不需要被剪枝
private boolean isValid(int row, int col) { // 传入行列
for (int i = 0; i < row; i++) {
// 如果之前某一行的皇后所在的列，正好等于当前列
// 说明这一列上有皇后了，不能摆
if (cols[i] == col) return false;
// 检查斜线，斜率法，直线方程检查，斜率绝对值等1
// 此处 当前行 - 先前行 row - i一定是正的， 列相减正负为止，为了适配斜线，加个绝对值
if (row - i == Math.abs(col - cols[i])) return false;
}
return true ;
}
public static void main(String[] args) {
new EightQueens().placeQueens(4); // expect 2
new EightQueens().placeQueens(8); // expect 92
}
}
运行结果
当前为 [4] 皇后问题，共有 [2] 种摆法
当前为 [8] 皇后问题，共有 [92] 种摆法

添加显示方法

写一个方法，来图形化的打印棋盘情况

添加了显示方法的代码
/**
* 八皇后问题 —— 回溯法
*/
public class EightQueens {
int[] cols; // 数组索引时行号，数组元素是列号，用来记录皇后摆放的位置
int numOfSolutions; // 可用摆法计数
// 摆放n个皇后的方法
public void placeQueens(int n) {
if (n < 1) return;
// 在 第0行 摆放第一个皇后
cols = new int[n]; // 初始化位置数组
place(0);
// 走到这里，说明所有递归调动结束了
System.out.println("当前为 [" + n + "] 皇后问题，共有 [" + numOfSolutions + "] 种摆法");
}
// 从第 row 行开始摆放1皇后
public void place(int row) {
// 递归退出条件，如果row == n，即8，说明所有的皇后已经摆好了
if (row == cols.length) {
// 结果集+1，退出递归
numOfSolutions++;
show();
return;
}
// 遍历一行中的所有列
for (int col = 0; col < cols.length; col++) { // 从第0列到第8列
// 查看哪个位置能摆
if (isValid(row, col)) { // 合法、有效、可以摆放皇后
// 能摆，那就摆
cols[row] = col;
// 摆完，立刻摆下一行
place(row + 1);
// 能执行到这个位置，发生回溯，走下一列了
}
// 来到这里，表示非法，无效，不能摆放皇后，就剪枝，剪枝就啥也不干
}
}
// 检查国际象棋规则的方法，用于剪枝
// 传入行列，确定一个唯一的格子，返回这个格子需不需要被剪枝
private boolean isValid(int row, int col) { // 传入行列
for (int i = 0; i < row; i++) {
// 如果之前某一行的皇后所在的列，正好等于当前列
// 说明这一列上有皇后了，不能摆
if (cols[i] == col) return false;
// 检查斜线，斜率法，直线方程检查，斜率绝对值等1
// 此处 当前行 - 先前行 row - i一定是正的， 列相减正负为止，为了适配斜线，加个绝对值
if (row - i == Math.abs(col - cols[i])) return false;
}
return true;
}
private void show() {
StringBuilder sb = new StringBuilder();
for (int row = 0; row < cols.length; row++) {
for (int col = 0; col < cols.length; col++) {
if (cols[row] == col) sb.append(" 1");
else sb.append(" 0");
}
sb.append("\n");
}
System.out.println(sb.toString());
}
public static void main(String[] args) {
new EightQueens().placeQueens(4); // expect 2
new EightQueens().placeQueens(8); // expect 92
}
}
执行结果
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
当前为 [4] 皇后问题，共有 [2] 种摆法
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 1 0 0 0 0 0
// 太多了省略
当前为 [8] 皇后问题，共有 [92] 种摆法

观察回溯过程

在isValid方法中进行打印，观察回溯过程

private boolean isValid(int row, int col) { // 传入行列
for (int i = 0; i < row; i++) {
// 如果之前某一行的皇后所在的列，正好等于当前列
// 说明这一列上有皇后了，不能摆
if (cols[i] == col) {
System.out.println("[" + row + "][" + col + "] = false");
return false;
}
// 检查斜线，斜率法，直线方程检查，斜率绝对值等1
// 此处 当前行 - 先前行 row - i一定是正的， 列相减正负为止，为了适配斜线，加个绝对值
if (row - i == Math.abs(col - cols[i])) return false;
}
// 打印，观察回溯
System.out.println("[" + row + "][" + col + "] = true");
return true;
}
执行结果
[0][0] = true
[1][0] = false
[1][1] = false
[1][2] = true
[2][0] = false
[2][1] = false
[2][2] = false
[2][3] = false
[1][3] = true
[2][0] = false
[2][1] = true
[3][0] = false
[3][1] = false
[3][2] = false
[3][3] = false
[2][2] = false
[2][3] = false
[0][1] = true
[1][0] = false
[1][1] = false
[1][2] = false
[1][3] = true
[2][0] = true
[3][0] = false
[3][1] = false
[3][2] = true
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0
[3][3] = false
[2][1] = false
[2][2] = false
[2][3] = false
[0][2] = true
[1][0] = true
[2][0] = false
[2][1] = false
[2][2] = false
[2][3] = true
[3][0] = false
[3][1] = true
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
[3][2] = false
[3][3] = false
[1][1] = false
[1][2] = false
[1][3] = false
[0][3] = true
[1][0] = true
[2][0] = false
[2][1] = false
[2][2] = true
[3][0] = false
[3][1] = false
[3][2] = false
[3][3] = false
[2][3] = false
[1][1] = true
[2][0] = false
[2][1] = false
[2][2] = false
[2][3] = false
[1][2] = false
[1][3] = false
当前为 [4] 皇后问题，共有 [2] 种摆法

代码优化——布尔数组

针对isValid进行优化

  • 目前：对每个单独的格子，都要运行循环，对当前所有行进行检查

    • 原因在于先前使用数组cols，用索引表示行，元素表示皇后所在的列

  • 现在：用3个布尔类型的数组来存储

    • boolean[] cols——标记某一列是否有皇后了
    • boolean[] leftTop_righBottom——标记某一对角线上是否有皇后了，左上角到右下角
    • boolean[] rightTop_leftBottom——标记某一对角线上是否有皇后了，右上角到左下角

  • isValid方法

    • 直接查询对应列有没有皇后

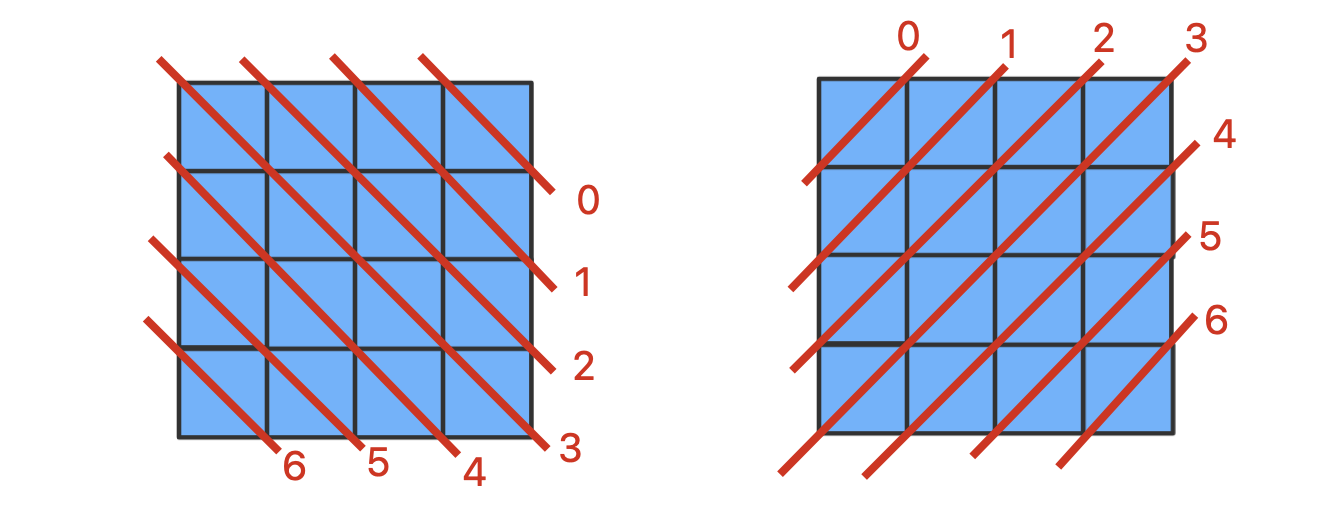
    • 检查斜线，用两个布尔类型的数组来做，如下图所示，这两个数组的长度为2n - 1

      • 如何知道是哪一根对角线？

        • 对于左上角到右下角：根据row - col的差值，以四皇后为例，row - col的差值可以取-3 -2 -1 0 1 2 3七种，为了使用数组，我们需要把这个区间平移到以0开始，显然加上n - 1就可以，对于四皇后，n == 4，则采用row - col + 4 - 1，得到差值0 1 2 3 4 5 6
          • 用这一组差值作为数组的索引，按顺序表示对应的对角线，以左上到右下的对角线为例，索引为0的就表示最靠右上角的对角线，索引为6表示最靠左下角的对角线
        • 对于右上角到左下角：索引为row + col，得到0 1 2 3 4 5 6

    • 如果有效，就摆皇后，在这种情况下，3个数组都要摆

    • 如果无效剪枝，此时利用continue跳出本次循环即可

    • 如果发生回溯，对于布尔类型，需要重置上一个格子的值

问题

为什么之前的写法不用在回溯位置进行恢复现场？

  • 因为之前用cols[i]标记第i行的某列有皇后，回溯之后，cols[i]的值会被新值覆盖
  • 此处的写法使用布尔类型数组，标记了整列，整条对角线，这个没办法覆盖，必须手动恢复状态
使用3个布尔数组的优化写法
/**
* 在上一版基础上进行优化
*/
public class EightQueens2 {
int[] queens; // 仅用作存储最终摆放位置，方便打印
boolean[] cols; // 索引表示列，元素表示列是否有皇后
boolean[] leftTop_rightBottom; // ↖↘ 对角线上是否有皇后
boolean[] rightTop_leftBottom; // ↗↙ 对角线上是否有皇后
int numOfSolutions; // 可用摆法计数
// 摆放n个皇后的方法
public void placeQueens(int n) {
if (n < 1) return;
// 在 第0行 摆放第一个皇后
queens = new int[n]; // 初始化摆放结果数组，仅用于打印
cols = new boolean[n]; // 初始化位置数组
leftTop_rightBottom = new boolean[(n << 1) - 1]; // 初始化对角线 2n - 1
rightTop_leftBottom = new boolean[leftTop_rightBottom.length]; // 初始化对角线 2n - 1
place(0);
// 走到这里，说明所有递归调动结束了
System.out.println("当前为 [" + n + "] 皇后问题，共有 [" + numOfSolutions + "] 种摆法");
}
// 从第 row 行开始摆放1皇后
public void place(int row) {
// 递归退出条件，如果row == n，即8，说明所有的皇后已经摆好了
if (row == cols.length) {
// 结果集+1，退出递归
numOfSolutions++;
show();
return;
}
// 遍历一行中的所有列
for (int col = 0; col < cols.length; col++) { // 从第0列到第8列
// 查看哪个位置能摆
// 直接检查对应列有没有皇后
if (cols[col]) {
System.out.println("[" + row + "][" + col + "] = false");
continue;
}
// 检查斜线
// 左上角右下角斜线上有皇后
int leftTop_rightBottom_index = row - col + cols.length - 1;
if (leftTop_rightBottom[leftTop_rightBottom_index]) {
System.out.println("[" + row + "][" + col + "] = false");
continue;
}
int rightTop_leftBottom_index = row + col;
if (rightTop_leftBottom[rightTop_leftBottom_index]) {
System.out.println("[" + row + "][" + col + "] = false");
continue;
}
// 能摆，那就摆, 此时另外两个数组也要摆
System.out.println("[" + row + "][" + col + "] = true");
queens[row] = col; // 存储一下摆放位置，仅用于打印
cols[col] = true;
leftTop_rightBottom[leftTop_rightBottom_index] = true;
rightTop_leftBottom[rightTop_leftBottom_index] = true;
// 摆完，立刻摆下一行
place(row + 1);
// 能执行到这个位置，发生回溯，走下一列了
// 对于布尔类型，重置上一个格子的值
cols[col] = false;
leftTop_rightBottom[leftTop_rightBottom_index] = false;
rightTop_leftBottom[rightTop_leftBottom_index] = false;
}
}
// 检查国际象棋规则的方法，用于剪枝
// 传入行列，确定一个唯一的格子，返回这个格子需不需要被剪枝
/*private boolean isValid(int row, int col) { // 传入行列
// 直接检查对应列有没有皇后
if (cols[col]) {
System.out.println("[" + row + "][" + col + "] = false");
return false;
}
// 检查斜线
if (leftTop_rightBottom[leftTop_rightBottom_index]) {
// 左上角右下角斜线上有皇后
return false;
}
if (rightTop_leftBottom[rightTop_leftBottom_index]) {
return false;
}
// 打印，观察回溯
System.out.println("[" + row + "][" + col + "] = true");
return true;
}*/
private void show() {
StringBuilder sb = new StringBuilder();
for (int row = 0; row < cols.length; row++) {
for (int col = 0; col < cols.length; col++) {
/* if (queens[row] == col) sb.append(" 1");
else sb.append(" 0");*/
sb.append(queens[row] == col ? " 1" : " 0");
}
sb.append("\n");
}
System.out.println(sb.toString());
}
public static void main(String[] args) {
new EightQueens2().placeQueens(4); // expect 2
// new EightQueens().placeQueens(8); // expect 92
}
}

代码优化——位运算

可以利用位运算，进一步压缩空间复杂度

  • 该方法只用于数据规模较小的情况，最好n <= 8
  • 以八皇后为例
  • 不使用布尔数组，直接使用8位二进制数byte
  • 看对应二进制位的0和1来表示先前布尔的false和true
    • 用8位二进制数 按位与 上1左移列数，如果等于0就可以放；不等于0就说明那位上有值，进行剪枝
    • 放置皇后，就是将对应二进制位设置为1，采用按位或可以做到
    • 回溯时，将对应为恢复，对应为和0与，其他为和1与，为了方便实现，可以将1先左移到达目标位置，然后把这个数取反，再和之前的数据进行与
位运算写法
/**
* 位运算优化
*/
public class EightQueens3 {
int[] queens; // 仅用作存储最终摆放位置，方便打印
byte cols; // 索引表示列，元素表示列是否有皇后 8位
short leftTop_rightBottom; // ↖↘ 对角线上是否有皇后 15位，用两个字节
short rightTop_leftBottom; // ↗↙ 对角线上是否有皇后 15位，用两个字节
int numOfSolutions; // 可用摆法计数
// 摆放n个皇后的方法
public void placeEightQueens() {
// 在 第0行 摆放第一个皇后
queens = new int[8]; // 初始化摆放结果数组，仅用于打印
place(0);
// 走到这里，说明所有递归调动结束了
System.out.println("当前为 [8] 皇后问题，共有 [" + numOfSolutions + "] 种摆法");
}
// 从第 row 行开始摆放1皇后
public void place(int row) {
// 递归退出条件，如果row == 8，说明所有的皇后已经摆好了
if (row == 8) {
// 结果集+1，退出递归
numOfSolutions++;
show();
return;
}
// 遍历一行中的所有列
for (int col = 0; col < 8; col++) { // 从第0列到第8列
// 查看哪个位置能摆
// 直接检查对应列有没有皇后
if ((cols & (1 << col)) != 0) continue;
// 检查斜线
// 左上角右下角斜线上有皇后
int leftTop_rightBottom_index = row - col + 7;
if ((leftTop_rightBottom & (1 << leftTop_rightBottom_index)) != 0) continue;
int rightTop_leftBottom_index = row + col;
if ((rightTop_leftBottom & (1 << rightTop_leftBottom_index)) != 0) continue;
// 能摆，那就摆, 此时另外两个数组也要摆
queens[row] = col; // 存储一下摆放位置，仅用于打印
cols |= (1 << col);
leftTop_rightBottom |= (1 << leftTop_rightBottom_index);
rightTop_leftBottom |= (1 << rightTop_leftBottom_index);
// 摆完，立刻摆下一行
place(row + 1);
// 能执行到这个位置，发生回溯，走下一列了
cols &= ~(1 << col);
leftTop_rightBottom &= ~(1 << leftTop_rightBottom_index);
rightTop_leftBottom &= ~(1 << rightTop_leftBottom_index);
}
}
private void show() {
StringBuilder sb = new StringBuilder();
for (int row = 0; row < 8; row++) {
for (int col = 0; col < 8; col++)
sb.append(queens[row] == col ? " 1" : " 0");
sb.append("\n");
}
System.out.println(sb.toString());
}
public static void main(String[] args) {
new EightQueens3().placeEightQueens(); // expect 92
}
}
1 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0
// 省略
当前为 [8] 皇后问题，共有 [92] 种摆法