Version: Next

快速排序

1960 年由查尔斯·安东尼·理查德·霍尔 Charles Antony Richard Hoare，昵称 东尼霍尔 Tony Hoare

执行流程

执行流程

  • 从序列中选择一个 轴点元素 (Pivot)
    • 假设每次选择 index = 0 位置的 元素
  • 利用 pivot 将序列分割为 2 个子序列
    • 将 小于 pivot 的放在左侧
    • 将 大于 pivot 的放在右侧
    • 将 等于 pivot 放在任意一侧
  • 对两个子序列重复进行以上操作，直到不能再分割，即子序列中只剩下一个元素


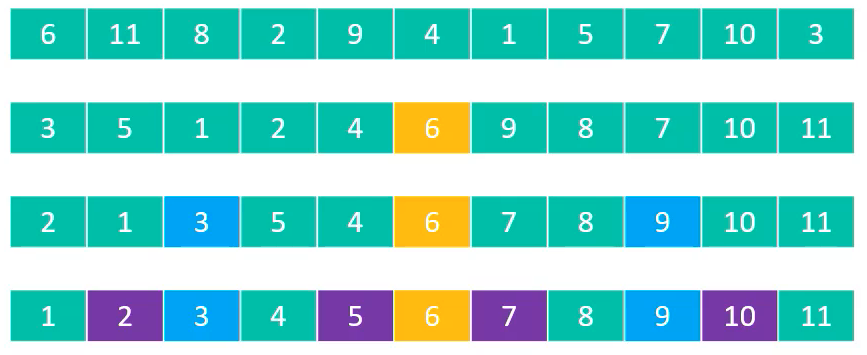
本质

逐渐将每一个元素都转换成轴点元素

轴点构造

为什么构造

根据快速排序的本质，就是将每一个元素都变成轴点，那么只要解决如何把一个元素变成轴点即可

  1. 先将希望成为轴点的元素 备份
  2. 确定最终轴点对应的 index
  3. 从尾向头扫描，对比每一个元素与轴点元素的值大小，以 小值在轴点左，大值在轴点右 的原则
    1. 尾指针指向元素 大于 轴点值，则直接尾指针向左移动
    2. 尾指针指向元素 小于 轴点值，用尾指针指向元素覆盖头指针元素，头指针右移，转换为从头向尾扫描，此时尾指针指向的元素就是 垃圾数据，因为它已经被复制到头指针上去了
    3. 等于 的情况也进行交换，这可以保证子序列的均匀切割
  4. 从头向尾扫描
    1. 头指针指向元素 小于 轴点值，则直接头指针向右移动
    2. 头指针指向元素 大于 轴点值，将头指针指向元素覆盖到尾指针，尾指针左移，转换为从尾向头扫描
    3. 等于 的情况也进行交换
  5. 当 头尾指针 相等，说明 一个 轴点构造完毕，此时把一开始备份的轴点元素值拿过来，覆盖 头(尾)指针指向的元素
  6. 返回当前头（尾）指针的 index，用于后续递归调用
  7. 对左右子序列递归调用，子序列元素只剩1个时退出递归

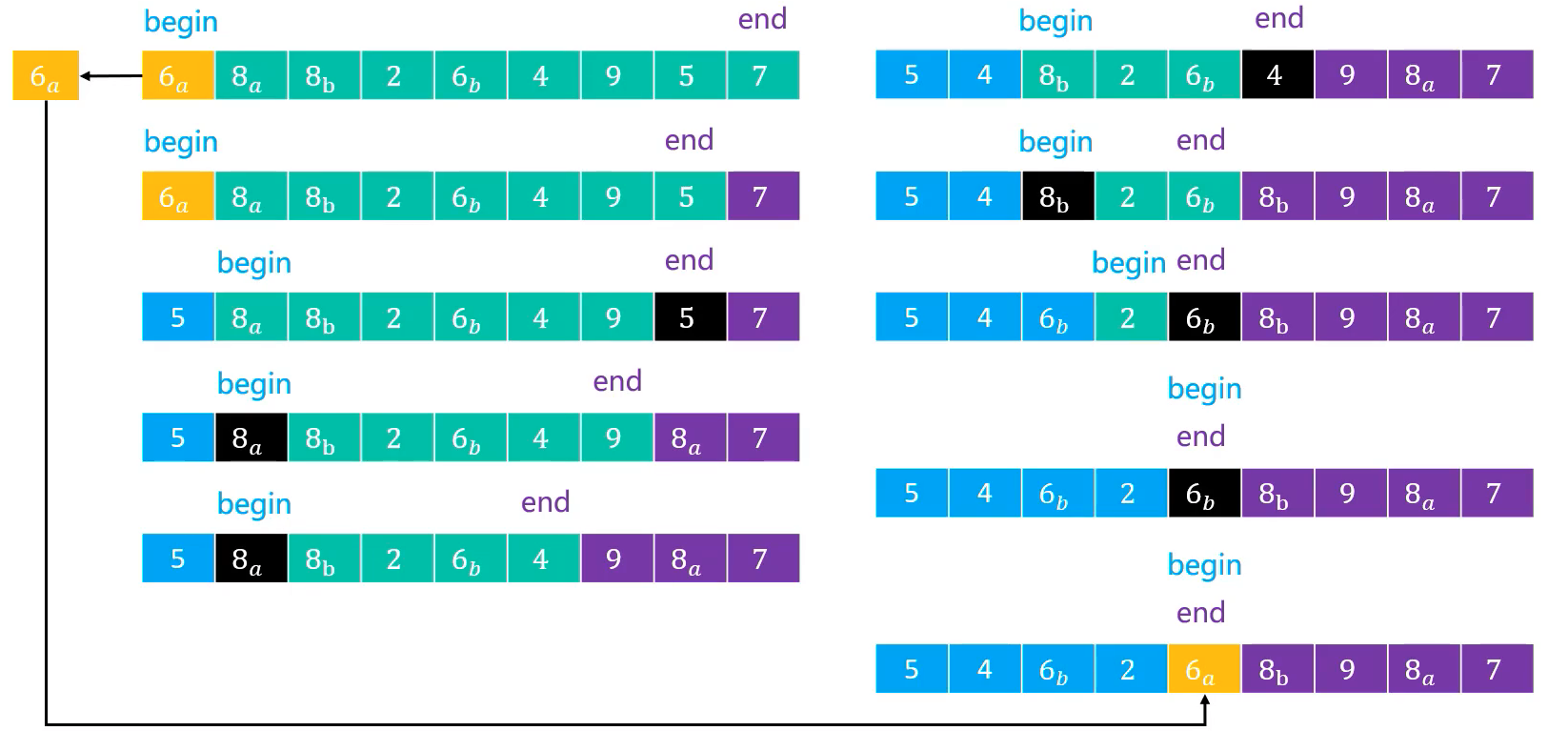
image-20210330150951002


实现

/**
* 快速排序
*/
public class QuickSort<E extends Comparable<E>> extends Sort<E> {
public QuickSort(E[] array) {
this.array = array;
}
@Override
public void sort() {
quickSort(0, array.length);
}
// [begin, end) 范围元素进行快速排序
private void quickSort(int begin, int end) {
// 递归机，只剩下一个元素时，就不能再切割了
if (end - begin < 2) return;
// 轴点构造
int pivot = pivotConstruct(begin, end);
// 对子序列进行递归
quickSort(begin, pivot);
quickSort(pivot + 1, end);
}
/**
* 根据范围，构造轴点，确定轴点最终的下标
*
* @param begin 头指针
* @param end 尾指针
* @return 轴点 index
*/
private int pivotConstruct(int begin, int end) {
// 随机选择轴点,begin + 随机步长
swap(begin, begin + (int) (Math.random() * (end - begin)));
// 备份 begin
E pivot = array[begin];
end--; // end 指向最后一个元素
while (begin < end) { // 只要 头指针 小于 尾指针
while (begin < end) {
// 从尾向头扫描
if (cmp(array[end], pivot) > 0) { // 右侧大于轴点
// 尾指针左移
end--;
} else { // 右侧小于等于
// 值覆盖头指针元素 头指针右移
array[begin++] = array[end];
break;
}
}
while (begin < end) {
// 从左往右扫描
if (cmp(array[begin], pivot) < 0) {
begin++;
} else {
array[end--] = array[begin];
break;
}
}
}
// begin == end
array[begin] = pivot; // 轴点元素归位覆盖
return begin; // begin 或 end 都是当前轴点下标
}
public static void main(String[] args) {
Integer[] array = {5, 3, 1, 2, 4};
QuickSort<Integer> integerQuickSort = new QuickSort<>(array);
integerQuickSort.sort();
for (Integer integer : array) {
System.out.print(integer + " ");
}
}
}

复杂度分析

  • 属于不稳定排序
    • 6a 、 6b 的位置发生了倒换

轴点左右元素均匀

  • 构造轴点，线性遍历 O(n)
  • 快速排序：假设为 T(n)则，T(n) = 2 * T(n / 2) + O(n)
    • 显然结果为 O(nlogn)
    • 前提是左右子序列比较均匀，否则不能认定为 T(n/2)

轴点左右极不均匀

  • 最坏情况：T(n) = T(n - 1) + O(n) = O(n ^ 2)

避免最坏情况

  • 随机选择轴点元素即可
  • 将 begin 与 begin+随机步长 位置的元素进行交换，然后开始快速排序

空间复杂度

  • 递归调用，空间复杂度 O(logn)