Version: Next
二叉树遍历
根据节点访问书序的不同,二叉树有4种常见遍历方式
- 前序遍历 (Preorder Traversal)
- 中序遍历 (Inorder Traversal)
- 后序遍历 (Postorder Traversal)
- 层序遍历 (Level Order Traversal)
前序遍历
递归访问
- 访问根节点
- 访问左子树
- 访问右子树
前序遍历实现
/**
* 前序遍历
*
* @param node 根节点
*/
private void preorderTraversal(Node<E> node) {
if (node == null) return;
System.out.println(node.element); // 先打印自己
preorderTraversal(node.leftNode); // 再打印左子树
preorderTraversal(node.rightNode); // 再打印右子树
}
public void preorderTraversal() {
preorderTraversal(rootNode);
}
前序遍历测试
private static void preorderTest() {
Integer[] data = new Integer[]{
7, 4, 9, 2, 5, 8, 11, 3
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
// 前序遍历
bst.preorderTraversal();
}
public static void main(String[] args) {
// integerTest();
// personTest();
// sameAgePersonTest();
preorderTest();
}
运行结果
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
7
4
2
3
5
9
8
11
中序遍历
访问顺序
- 访问左子树
- 访问根节点
- 访问右子树
info
对于二叉搜索树,中序遍历的输出结果为一个有序数列
- 左子树 -> 根节点 -> 右子树 : 升序
- 右子树 -> 根节点 -> 左子树 : 降序
中序遍历实现
/**
* 中序遍历
*
* @param node 根节点
*/
private void inorderTraversal(Node<E> node) {
if (node == null) return;
inorderTraversal(node.leftNode); // 打印左子树
System.out.println(node.element); // 打印自己
inorderTraversal(node.rightNode); // 打印右子树
}
public void inorderTraversal() {
inorderTraversal(rootNode);
}
中序遍历测试
private static void inorderTest() {
Integer[] data = new Integer[]{
7, 4, 9, 2, 5, 8, 11, 3
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
// 中序遍历
bst.inorderTraversal();
}
public static void main(String[] args) {
// integerTest();
// personTest();
// sameAgePersonTest();
// preorderTest();
inorderTest();
}
运行结果,可见输出为有序数列
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
2
3
4
5
7
8
9
11
后序遍历
访问顺序
- 访问左子树
- 访问右子树
- 访问根节点
后序遍历实现
/**
* 后序遍历
*
* @param node 根节点
*/
private void postorderTraversal(Node<E> node) {
if (node == null) return;
postorderTraversal(node.leftNode); // 打印左子树
postorderTraversal(node.rightNode); // 打印右子树
System.out.println(node.element); // 打印自己
}
public void postorderTraversal() {
postorderTraversal(rootNode);
}
后序遍历测试
private static void postorderTest() {
Integer[] data = new Integer[]{
7, 4, 9, 2, 5, 8, 11, 3
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
// 后序遍历
bst.postorderTraversal();
}
public static void main(String[] args) {
// integerTest();
// personTest();
// sameAgePersonTest();
// preorderTest();
// inorderTest();
postorderTest();
}
运行结果
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
3
2
5
4
8
11
9
7
层序遍历
不使用递归实现,一层一层访问
- 从上往下,从左往右依次访问每一个节点
- 使用
队列:
- 最
先被访问的节点,其子节点(子树)就是最先被访问的子节点(子树),即先进先出FIFO
实现思路
- 将根节点入队
- 循环执行以下操作,直到队列为空
- 将队头节点A出队,进行访问
- 将A节点的左子节点入队
- 将A节点的右子节点入队
层序遍历实现
/**
* 层序遍历
*/
private void levelOrderTraversal(Node<E> node) {
if (node == null) return;
// 维护一个队列,队列里的内容
Queue<Node<E>> queue = new LinkedList<>();
// 1. 将根节点入队, offer方法
queue.offer(rootNode);
// 2. 循环执行,直到队列为空
while (!queue.isEmpty()) {
// 2.1 将队头节点A出队,访问
Node<E> head = queue.poll();
System.out.println(head.element); // 访问
// 2.2 将A节点的左子节点入队
if (head.leftNode != null) queue.offer(head.leftNode);
// 2.3 将A节点的右子节点入队
if (head.rightNode != null) queue.offer(head.rightNode);
}
}
public void levelOrderTraversal() {
levelOrderTraversal(rootNode);
}
层序遍历测试
private static void levelOrderTest() {
Integer[] data = new Integer[]{
7, 4, 9, 2, 5, 8, 11, 3
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
// 层序遍历
bst.levelOrderTraversal();
}
public static void main(String[] args) {
// integerTest();
// personTest();
// sameAgePersonTest();
// preorderTest();
// inorderTest();
// postorderTest();
levelOrderTest();
}
运行结果,可见从上到下,从左到右打印
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
7
4
9
2
5
8
11
3
自定义遍历逻辑
如何设计二叉树遍历接口?
问题:
- 上述代码在遍历二叉树时写死了操作逻辑,即遍历到每一个节点,操作为:
打印节点的值- 实际上在遍历二叉树时,往往存在不同的需求,可能是对节点的值求和,可能是根据一些条件过滤节点等,如何支持这种个性化定制
解决:
- 可以参考先前传入外部比较器Comparator的模式,在二叉树内部定义一个接口
Visitor<E>,定义接口抽象方法visit(E element)要求传入二叉树存储的数据类型对象- 针对四种遍历方法,添加接收
Vistor<E>参数的遍历方法- 在外部书写匿名内部类或者lambda表达式实现
Vistor接口的visit(E element)方法,自定义遍历规则- 在遍历方法中,访问节点的代码(原System.out.println)更换为调用接口中的方法
visit(E element)
info
以层序遍历为例
定义一个内部接口Vistor<E>
/**
* 个性化遍历接口
*
* @param <E> 二叉树中存储的数据类型
*/
public static interface Visitor<E> {
/**
* 定义如何访问节点的内容
*
* @param element 树节点中的某个存储数据类的对象
*/
void visit(E element);
}
新的二叉树遍历方法,要求传入一个Visitor<E>接口的实现类对象
/**
* 层序遍历,要求传入个性化的遍历访问规则
*
* @param visitor 实现了Visitor接口的类对象
*/
public void levelOrder(Visitor<E> visitor) {
if (rootNode == null || visitor == null) return;
// 维护一个队列
Queue<Node<E>> queue = new LinkedList<>();
// 根节点入队
queue.offer(rootNode);
// 循环,直到队列为空
while (!queue.isEmpty()) {
// 队头A节点出队,并访问
Node<E> head = queue.poll();
//使用接口方法,执行外部传入的个性化遍历访问逻辑
visitor.visit(head.element);
// A节点的左节点入队
if (head.leftNode != null) queue.offer(head.leftNode);
// A节点的右节点入队
if (head.rightNode != null) queue.offer(head.rightNode);
}
}
自定义遍历规则测试,求和使用了JUC原子类确保lambda外部可以访问
private static void levelOrderVisitorTest() {
Integer[] data = new Integer[]{
7, 4, 9, 2, 5, 8, 11, 3
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
// 自定义遍历访问规则,lambda表达式实现接口方法
// 第一种规则:打印值,并且带上一句说明文字,说明这是外部传入的规则
Visitor<Integer> visitor1 = (element) -> System.out.println("外部传入规则:" + element);
// 第二种规则:遍历过程中,对每个节点的值进行累加求和
AtomicInteger sum = new AtomicInteger();
sum.set(0);
Visitor<Integer> visitor2 = (element) -> {
sum.addAndGet(element);
System.out.println("sum = " + sum);
};
// 自定义规则的层序遍历
// 使用规则1遍历
bst.levelOrderTraversal(visitor1);
// 使用规则2遍历
bst.levelOrderTraversal(visitor2);
}
运行结果
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
外部传入规则:7
外部传入规则:4
外部传入规则:9
外部传入规则:2
外部传入规则:5
外部传入规则:8
外部传入规则:11
外部传入规则:3
sum = 7
sum = 11
sum = 20
sum = 22
sum = 27
sum = 35
sum = 46
sum = 49
自定义遍历增强——不完全遍历
需求:
- 上述代码一旦开始遍历二叉树,必须遍历完整棵二叉树
- 如果调用者不希望完全遍历整棵二叉树,例如:遍历二叉树输出前5个节点,那么应该如何设计接口
解决方案:
- 修改
Visitor接口的void visit(E element)方法,修改返回类型为boolean,即boolean visit(E element)
- 如果返回
true,就停止遍历- 如果返回
false,就继续遍历(当然可以按自己的喜好定义)
层序遍历的情况
修改自定义遍历接口中抽象方法的返回值类型为boolean
/**
* 个性化遍历接口
*
* @param <E> 二叉树中存储的数据类型
*/
public static interface Visitor<E> {
/**
* 定义如何访问节点的内容
*
* @param element 树节点中的某个存储数据类的对象
* @return 是否继续遍历 false继续 true停止
*/
boolean visit(E element);
}
在调用接口方法进行访问之后,接收返回的布尔类型,决定是否停止遍历
/**
* 层序遍历,要求传入个性化的遍历访问规则
*
* @param visitor 实现了Visitor接口的类对象
*/
public void levelOrderTraversal(Visitor<E> visitor) {
if (rootNode == null || visitor == null) return;
// 维护一个队列
Queue<Node<E>> queue = new LinkedList<>();
// 根节点入队
queue.offer(rootNode);
// 循环,直到队列为空
while (!queue.isEmpty()) {
// 队头A节点出队,并访问
Node<E> head = queue.poll();
//使用接口方法,执行外部传入的个性化遍历访问逻辑
boolean stopFlag = visitor.visit(head.element);
// 如果返回true,停止遍历
if (stopFlag) return;
// A节点的左节点入队
if (head.leftNode != null) queue.offer(head.leftNode);
// A节点的右节点入队
if (head.rightNode != null) queue.offer(head.rightNode);
}
}
测试:定义当节点值等于2时停止遍历
private static void levelOrderVisitorTest() {
Integer[] data = new Integer[]{
7, 4, 9, 2, 5, 8, 11, 3
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
// 自定义遍历访问规则,lambda表达式实现接口方法
// 第一种规则:打印值,并且带上一句说明文字,说明这是外部传入的规则
Visitor<Integer> visitor = (element) -> {
System.out.println("外部规则:" + element);
// 当节点值为2时,停止遍历
// return element == 2 ? true : false;
return element == 2;
};
// 自定义规则的层序遍历
// 使用规则1遍历
bst.levelOrderTraversal(visitor);
}
执行结果:可见当遍历到值为2的节点时,遍历终止
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
外部规则:7
外部规则:4
外部规则:9
外部规则:2
前(中、后)序遍历的情况
问题:
- 这三种遍历的代码中,采用的是递归,而不是while循环,因此,终止遍历不能像层序遍历那样直接跳出while循环
- 需要一个
stopFlag来记录每一次方法被执行时的停止递归标志,这个布尔类型的stopFlag应该定义在哪里呢?
- 不能定义为二叉树的成员变量:
- 原因1:因为一棵二叉树涉及前序遍历、中序遍历、后序遍历、层序遍历等多种遍历方式,如果使用成员变量的话,就需要多个布尔类型的变量;
- 原因2:在多线程情况下存在线程安全问题
- 定义在
Visitor接口的实现类对象中
- 每一次方法调用都有一个独立的
stopFlagstopFlag作为成员变量,但接口的成员变量省略了修饰public static final,即只能是常量,不能是变量- 由上一条所述,修改
interface Visitor为abstract class Visitor,将接口修改为抽象类,将方法修饰为抽象方法,与接口相比,抽象类可以定义成员变量- 由上一条所述,
Visitor由接口修改为抽象类,则不再是函数式接口,因此不能再使用lambda表达式,必须采用匿名内部类进行实例化
修改接口Visitor为抽象类Visitor,添加一个成员变量stopFlag,修改visit方法为接口方法
/**
* 个性化遍历接口
*
* @param <E> 二叉树中存储的数据类型
*/
public static abstract class Visitor<E> {
boolean stopFlag = false;
/**
* 定义如何访问节点的内容
*
* @param element 树节点中的某个存储数据类的对象
* @return 是否继续遍历 false继续 true停止
*/
abstract boolean visit(E element);
}
可自定义遍历规则的前序遍历方法
/**
* 可自定义遍历规则的前序遍历
* @param node 传入的树节点
* @param visitor 自定义遍历规则,抽象类Visitor的实例化对象
*/
public void preorderTraversal(Node<E> node, Visitor<E> visitor) {
if (node == null) return;
// 如果stopFlag为true,则不进行递归,即跳出遍历
if (visitor.stopFlag) return;
// 记录每次执行访问方法后的返回布尔类型值
visitor.stopFlag = visitor.visit(node.element);
preorderTraversal(node.leftNode, visitor);
preorderTraversal(node.rightNode, visitor);
}
测试,接口变抽象类,函数式接口失效,lambda失效,必须使用匿名内部类;遍历到值为5的节点就停止
private static void preorderVisitorTest() {
Integer[] data = new Integer[]{
7, 4, 9, 2, 5, 8, 11, 3
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
// 自定义遍历规则
Visitor<Integer> visitor = new Visitor<Integer>() {
@Override
boolean visit(Integer element) {
System.out.println(element);
return element == 5; // 遍历到值为5的节点就停止
}
};
// 自定义规则前序遍历
bst.preorderTraversal(bst.rootNode, visitor);
}
运行结果:可见遍历到值为5的节点遍历就终止了
┌──7──┐
│ │
┌─4─┐ ┌─9─┐
│ │ │ │
2─┐ 5 8 11
│
3
7
4
2
3
5
再优化
问题:
- 对于中序遍历和后序遍历,上述的写法其实只是终止了抽象类
方法visit的执行,遍历的递归调用实际上并没有被终止,每一个节点都被递归调用了,只是进去以后进行了判断然后return;了
自定义规则后序遍历,可见两句递归调用并不能被有效终止
public void postorderTraversal(Node<E> node, Visitor<E> visitor) {
if (node == null) return;
preorderTraversal(node.leftNode, visitor);
preorderTraversal(node.rightNode, visitor);
// 如果stopFlag为true,则不进行递归,即跳出遍历
if (visitor.stopFlag) return;
// 记录每次执行访问方法后的返回布尔类型值
visitor.stopFlag = visitor.visit(node.element);
}
解决:
- 在判断节点是否为空
node == null时,也要判断visitor.stopFlag- 不能移除原先对visitor.stopFlag的判断,因为递归过程中(对子树的访问)可能就满足了终止递归的条件,两次判断确保第一时间终止遍历
优化后的自定义后序遍历提前终止遍历,两次判断stopFlag
public void postorderTraversal(Node<E> node, Visitor<E> visitor) {
if (node == null || visitor.stopFlag) return;
preorderTraversal(node.leftNode, visitor);
preorderTraversal(node.rightNode, visitor);
// 如果stopFlag为true,则不进行递归,即跳出遍历
if (visitor.stopFlag) return;
// 记录每次执行访问方法后的返回布尔类型值
visitor.stopFlag = visitor.visit(node.element);
}
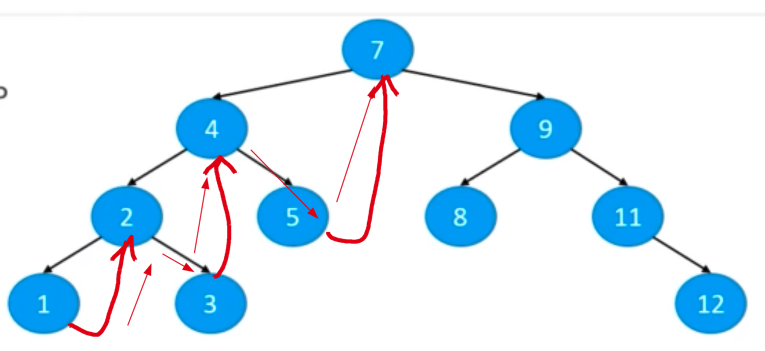
Morris中序遍历
为什么使用
使用 Morris 方法遍历二叉树,可以实现时间复杂度 O(n)、空间复杂度 O(1)
- 也称 线索二叉树
步骤(假设当前遍历到的节点是 N)
- 如果
N.left != null,就找到 N 的前驱节点 P
- 如果
P.right == null,则
- 令
P.right = N- 令
N = N.left- 回到
1.- 如果
P.right == N(开始中序打印)
P.right = null先前插入的线已经要被用了,所以可以删掉了- 打印N
N = N.right(向右遍历打印,看图,先前修改了各节点的 right 指针,于是此处等效于中序遍历)- 回到
1.- 如果
N.left == null,则
- 直接打印 N
N = N.right- 回到
1.
遍历的应用
前序遍历的应用
打印树
重写
toString()方法,采用前序遍历,配合字符串拼接
/**
* 利用前序遍历打印二叉树
*/
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
toString(rootNode, sb, "");
return sb.toString();
}
private void toString(Node<E> node, StringBuilder sb, String prefix) {
if (node == null) return;
sb.append(prefix).append(node.element).append("\n");
toString(node.leftNode, sb, prefix + "左 ");
toString(node.rightNode, sb, prefix + "右 ");
}
测试
// 前序遍历实现打印树
private static void preorderPrintTree() {
Integer[] data = new Integer[]{
4, 2, 1, 3, 6, 5, 7
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
System.out.println(bst);
}
运行结果
┌──4──┐
│ │
┌─2─┐ ┌─6─┐
│ │ │ │
1 3 5 7
4
左 2
左 左 1
左 右 3
右 6
右 左 5
右 右 7
中序遍历的应用
二叉搜索树的中序遍历按照升序或降序形成数列
后序遍历的应用
适用于一些先子后父的操作
层序遍历的应用
- 计算二叉树的高度
- 判断一棵树是否为完全二叉树
计算二叉树的高度
高度:根节点到最远叶子节点的高度,根节点的高度也就是树的高度
- 递归法
某节点的高度 = max (左节点高度,右节点高度) + 1- 迭代法
- 层序遍历:
树高度 = 树层数,维护一个队列- 每当访问完一层时,
下一层的节点个数 = 队列的长度size- 访问完一层时,高度 + 1
递归法
/**
* 返回某个节点的高度
*
* @param node 要求哪个节点的高度
* @return 节点的高度
*/
public int height(Node<E> node) {
if (node == null) return 0; // ↓ 递归调用
return Math.max(height(node.leftNode), height(node.rightNode)) + 1;
}
/**
* 利用前序遍历打印二叉树
*/
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
toString(rootNode, sb, "");
return sb.toString();
}
迭代法
/**
* 层序遍历求树高度
*
* @return 树高度
*/
public int heightViaLevelOrder() {
if (rootNode == null) return 0;
int height = 0;
int levelSize = 1; // 行容量,层容量;默认只有一个根节点
// 维护一个队列
Queue<Node<E>> queue = new LinkedList<>();
// 根节点入队
queue.offer(rootNode);
// 循环 直到队列为空
while (!queue.isEmpty()) {
// 头A出队,访问
Node<E> head = queue.poll();
// 每从队列中取出一个节点,将行容量-1
levelSize--;
// A的左入队
if (head.leftNode != null) queue.offer(head.leftNode);
// A的右入队
if (head.rightNode != null) queue.offer(head.rightNode);
// 如果levelSize降为0,则此时下一层节点的个数 = 当前队列的长度Size
if (levelSize == 0) {
levelSize = queue.size();
height++;
}
}
return height;
}
测试
private static void treeHeightTest() {
Integer[] data = new Integer[]{
4, 2, 1, 3, 6, 5, 7
};
// 不传入外部比较器,使用Integer的Comparable比较,而Integer默认实现了Comparable接口
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
System.out.println("bst.height()递归法 = " + bst.height());
System.out.println("bst.height()迭代法 = " + bst.heightViaLevelOrder());
}
递归法运行结果
┌──4──┐
│ │
┌─2─┐ ┌─6─┐
│ │ │ │
1 3 5 7
bst.height()递归法 = 3
bst.height()迭代法 = 3
判断一棵树是否为完全二叉树
所有叶子节点分布在最后
2层,且所有叶子节点靠左对齐;即从上到下,从左到右节点依次排列的二叉树
- 使用
层序遍历:因为层序遍历和完全二叉树都是,从上到下从左到右的顺序
性质:
- 如果树不为空,开始层序遍历二叉树(基于队列)
- 如果
node.left != null && node.right != null,将node.left和node.right按顺序入队 (即允许度为2的节点)- 如果
node.left == null && node.right != null返回false,即不允许度为1且右对齐的节点- 如果
node.left != null && node.right == null即度为1,左对齐 ;或,node.left == null && node.rigt == null即度为0,那么:从这个节点开始,之后所有的节点都应为叶子节点(度为0)
完全二叉树判断
/**
* 判断是否为完全二叉树
* 层序遍历实现 因为 层序遍历 和 完全二叉树,都是从上到下从左到右的顺序
*
* @return 是否为完全二叉树
*/
public boolean isCompleteBinaryTree() {
if (rootNode == null) return false;
// 维护一个队列
Queue<Node<E>> queue = new LinkedList<>();
// 根入队
queue.offer(rootNode);
// 叶子节点标志
boolean isLeaf = false;
// 循环,直到队列为空
while (!queue.isEmpty()) {
// 队列头A出队,判断
Node<E> head = queue.poll();
// =============判断部分===============
// A*: 检查叶子标志是否已经为true,如果已经为true,应当确保之后的node都是叶子节点
if (isLeaf && !head.isLeaf())
return false; // 叶子标志已经为true,但节点还有子树,说明不是完全二叉树
if (head.hasTwoChildren()) {
//如果node.left != null && node.right != null,
// 将node.left和node.right按顺序入队 (即允许度为2的节点)
queue.offer(head.leftNode);
queue.offer(head.rightNode);
} else if (head.leftNode == null && head.rightNode != null) {
// 如果node.left == null && node.right != null返回false,即不允许度为1且右对齐的节点
return false;
} else if ((head.leftNode != null && head.rightNode == null)
|| (head.leftNode == null && head.rightNode == null)) {
// node.left != null && node.right == null 或者
// node.left == null && node.right == null
// 那么:从这个节点开始,之后所有的节点都应为叶子节点(度为0)
// 到达这个位置,一定是叶子节点
isLeaf = true; // 在 A*处进行检查
}
// =============判断部分===============
}
return true;
}
测试
private static void isCompleteBinaryTreeTest() {
Integer[] data = new Integer[]{
7, 4, 9, 2, 5
};
MyBinarySearchTree<Integer> bst = new MyBinarySearchTree<>();
// 添加
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
System.out.println("bst.isCompleteBinaryTree() = " + bst.isCompleteBinaryTree());
}
运行结果
bst.isCompleteBinaryTree() = true
对判断部分进行简化
优化写法
public boolean isCompleteBinaryTree2() {
if (rootNode == null) return false;
// 维护一个队列
Queue<Node<E>> queue = new LinkedList<>();
// 根入队
queue.offer(rootNode);
boolean isLeaf = false;
while (!queue.isEmpty()) {
Node<E> head = queue.poll();
if (isLeaf && !head.isLeaf()) return false;
if (head.leftNode != null) { // 左不为空
queue.offer(head.leftNode);
} else if (head.rightNode == null) { // 左为空,右也为空
return false;
}
if (head.rightNode != null) {
queue.offer(head.rightNode);
} else { // 右边为空,左边不论是否为空 -> 之后的节点都应该是叶子节点
isLeaf = true;
}
}
return true;
}
根据遍历结果重构二叉树
根据一颗二叉树遍历出来的结果,还原出二叉树的具体结构
- 以下结果可以保证重构出唯一的一颗二叉树
- 前序遍历 +
中序遍历- 后序遍历 +
中序遍历
原理:
前序遍历的结果[自己] [left] [right]中序遍历的结果[left] [自己] [right]
- 显然
前序遍历的第一个结果对应根节点- 在
中序遍历的结果中找到根节点,则左侧为左子树,右侧为右子树- 根据上一条确认出的中序遍历左子树、中序遍历右子树,可以在前序遍历结果中确认出前序遍历左子树,前序遍历右子树
- 重复1~3:前序遍历的子树还是前序遍历的,因此第一个节点就是前序遍历子树的根节点,根据这个根节点,又可以在中序遍历子树中确认出左右子树
例:
- 前序遍历:4 2 1 3 6 5
- 中序遍历:1 2 3 4 5 6
试着重构二叉树
前序的第一个数4是根节点
根据中序知,左子树包含123,右子树包含56
回到前序遍历的结果中,根据213知左子树的根为2;根据65知右子树的根为6
则
重构二叉树---4---| |--2-- --6| | |1 3 5
给出前序遍历 + 后序遍历 的情况:
- 如果二叉树时一颗
真二叉树,则结果是唯一的- 否则,结果不唯一
原因是搞不清楚左右子树