Version: Next
50.Pow(x, n)
难度 中等
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
提示:
-100.0 < x < 100.0-231 <= n <= 231-1-104 <= xn <= 104
快速幂(分治)
时间复杂度 O(logn)
空间复杂度:
- 递归:O(logn)
- 非递归:O(1)
递归
3^20 = 3^10 3^10 -> pow(x, n) = pow(x, n >> 1) pow(x, n >> 1)
3^21 = 3^10 3^10 3 -> pow(x, n) = pow(x, n >> 1) pow(x, n >> 1) x
public double myPow(double x, int n) {
if (n == -1) return 1.0 / x;
if (n == 0) return 1.0;
if (n == 1) return x;
double res;
// 最小的二进制位是1就是奇数,是0就是偶数
boolean isOdd = (n & 1) == 1; // 奇数标志
double half = myPow(x, n >> 1);
half *= half;
return isOdd ? (half * x) : half;
}
也可写成
public double myPow(double x, int n) {
long N = n;
return N > 0 ? pow(x, N) : 1.0 / pow(x, -N);
}
private double pow(double x, long y) {
if (y == 0) return 1.0;
double half = pow(x, y >> 1);
return (y & 1) == 1 ? half * half * x : half * half;
}
非递归
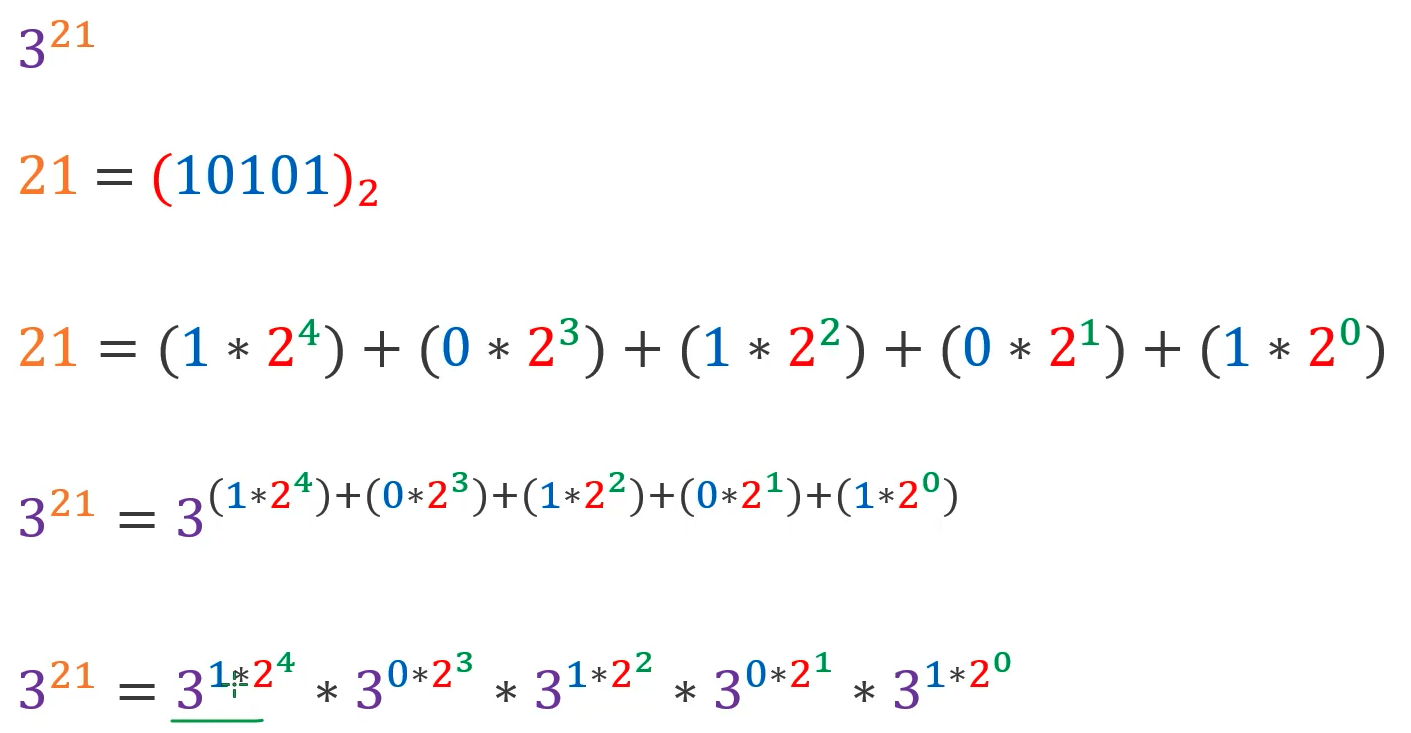
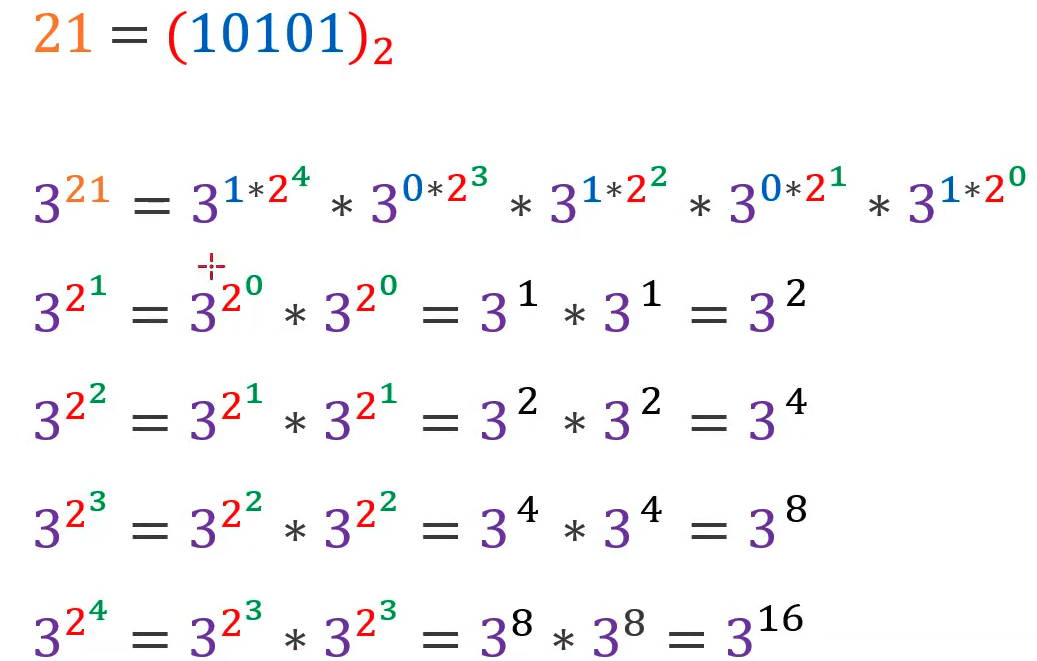
无负数的情况
public double myPow2(double x, int n) {
if (n == -1) return 1.0 / x;
if (n == 0) return 1.0;
if (n == 1) return x;
double res = 1.0;
while (n > 0) {
System.out.println(n & 1); // 打印 二进制 的最低位
if ((n & 1) == 1) res *= x;
// 计算下一个
x *= x;
// 舍弃最后一个二进制位
n >>= 1;
}
return res;
}
对于 n 为负数
- 先将 n 转为正数
- n 的范围为
[-2^31, 2^31 - 1],对于最小取值,取反以后,超出了 int 的表示范围,因此要使用 long 来存储 n- 最后用 1 除以运算结果
快速幂补充
请设计一个算法求 x 的 y 次幂模 z 的结果
x^y % z
- 假设 x, y, z 都可能是
很大的正数,溢出问题
- x ≥ 0, y ≥ 0, z ≠ 0
- 公式:
(a * b) % p == ((a % p) * (b % p)) % p// 求幂 再 取模public int powMod(int x, int y, int z) {if (x < 0 || y < 0 || z == 0) return 0;int res = 1 % z;x %= z;while (y > 0) {// 如果最后一个二进制是1,就累乘上 xif ((y & 1) == 1) res = (res * x) % z;x = (x * x) % z;// 舍弃最后一个二进制位y >>= 1;}return res % z;}